前回から間が空いてしまいましたが、ペースを上げての第4回です。前回からの続きでインデックスを扱います。その中でも特に、手品の種の部分にあたるインデックスのアルゴリズムに焦点を当てます。難しい話になるのではと心配されるかもしれませんが、大丈夫です。ここではアルゴリズムの特徴と特性を理解していただくのが目的で、その詳細についての難しい話はありません。ここで読んでいる皆さんはDBMSの開発者ではなく使用者でしょうから、特徴・特性をふまえてどのような使い方をするべきかを学んでください。
利用されるアルゴリズム
まずは、実際にどのようなアルゴリズムがどのくらい使われているか、というのを以下に示します。
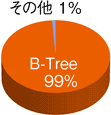
この図はあくまでもイメージです。しかし、B-Treeのみが圧倒的に使われているというのは本当に現実です。確かに、インデックス作成時に標準のままアルゴリズムをなにも指定しない場合、B-Treeで作られる場合が多いという面はあります。しかし、それ以上にこのインデックスは普遍的に使われるだけの良さを持っています。そこで、今回はまずB-Treeの特徴について説明します。これさえ分かれば世の中の99%のインデックスは理解したも同然です。
B-Tree
B-Treeインデックスは、その名のとおりB-Tree(B木)というアルゴリズムやその派生を使って実装されたインデックスです。Treeという名称に違わずツリー型の構造を持ったアルゴリズムです。ツリー型では、検索を逐次ではなく木構造をたどることで高速に出来るという特徴があります。
しかしながら、B-Treeそのものは非常に複雑なので、ここでは同じ木構造を持ち、同じように検索に用いられるものの中で、シンプルな二分探索木でその特性を説明しましょう。
二分探索木
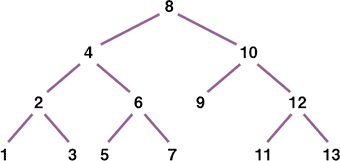
二分探索木は以下の図にあるような構造を持ったアルゴリズムです。すべてのノードは、以下のルールに従って格納されています。
- ノードは、必ず一つの値を持つ
- ノードは、最大二つの小ノードを持つ。おのおの左右に分かれており、親ノードよりも左側が「小さい」、右側が「大きい」値を持ったノードを格納する
二分探索木の例
二分探索木の検索
二分探索木における探索は、常に以下のルールによります。
- 一番頂上のノードから始めます。
- 検索したい値と、ノードに入っている場合を比較します。
- 一致した場合は当たりです。
- 検索したい値がノードの値より大きい場合、右側に移ります。逆に小さい場合は左側に移ります。
- 一致したものが見つかるまで続けます。
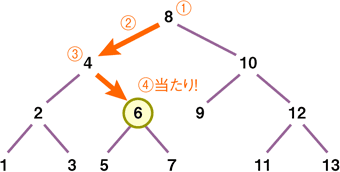
例えば、図において6を検索したい場合、
- 「8」のノードから始める(①)
- 「8」は6より大きいので、左側の子ノードに移る(②)
- 移った先の「4」は6より小さいので、右側の子ノードに移る(③)
- 移った先の「6」は6と等しいので、当たり!(④)
のようになり、全体が13個あるのに対して、8, 4, 6の3つだけの検索ですむようになります。
二分探索木の検索
さらにポイントとしては、二分探索木は値を順に並べているため、範囲検索も行うことが出来ます。
- 一番頂上のノードから始めます。
- 検索したい範囲のノードに入っているかを比較します。
- 最小値より大きい場合、左側をスキャンします。
- 範囲内の場合、自分を列挙します。
- 最大値より小さい場合、右側をスキャンします。
また、この場合、範囲にこだわらずにすべての値を列挙すれば値が順にそろうため、そのままソートとして扱うことも出来ます! 木構造のアルゴリズムは実に便利です。
挿入、更新、削除
検索が簡単で便利な反面、データの更新削除が非常に面倒なのが木構造の欠点です。
データを挿入する場合も削除する場合も、ひとまず検索を行って、実際に格納する場所や削除するエントリがどこになるかを確定します。
挿入の場合は、そのエントリの下に空きがあるはずですので、それを見て挿入します。
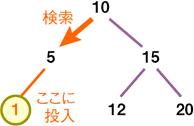
削除の場合には、実際に探し出したあと削除します。末端の場合は特に問題はありません。
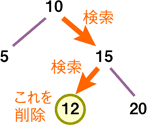
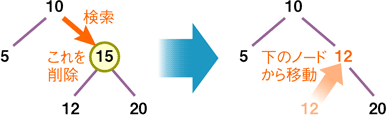
もし末端ではなく下にノードがある場合、いずれかのエントリを上位に昇格させる処理が必要になります。
更新はすなわち挿入と削除です。
戻ってB-Tree
戻ってB-Treeは、木構造で高速な検索を行う二分探索木の特徴を受け継ぎつつ、より複雑化したアルゴリズムです。ポイントとしては、
- ノードことに可変数のキーを格納するため、ノードをたどる回数が少なくて済む
- 記憶領域の利用効率が高く、50%以上を期待できる
- ハードディスクのような補助記憶装置に木構造を配置するのに非常に適している
といった点があげられます。PostgreSQLでは通常のB-Treeですが、それ以外にも改良型のB+-TreeやB*-Treeというアルゴリズムを使うことがあります。これらも基本的には似たようなものと言っていいでしょう。
また、B-Treeはより複雑化した結果、データの削除が非常に困難です。もちろん完全な削除を実装しているケースもあります。しかし、実装困難以外にも理由があったりして、単に「このデータは削除した」フラグをつけてごまかすケースも多いです。これは多くの場合、B-Treeインデックスが更新や削除を繰り返すことにより、削除フラグがついているだけのインデックスが多くなってしまい、肥大化してしまうことを意味します。
このような事情から、多くの実装ではインデックスを再作成するためのコマンドを用意していたりします。
まとめ
- インデックスは様々な種類がありますが、ほとんどB-Treeです。
- B-Treeはソート、範囲、一致検索に使え、ほとんどのケースをカバーします。
- ノードの削除が難しいため、肥大化する傾向があります。肥大化しないような手法を採用したものもあります。








