判断基準の推測 ~データからの学習~
これまでは合格基準が明らかになっている場合について考えてきました。続いて,
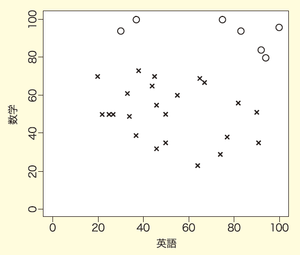
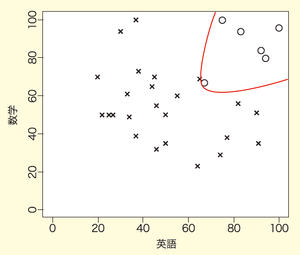
図4を見てください。この図における合格者と不合格者を分ける分類基準を推測してみましょう。
合格基準は1つではなく,
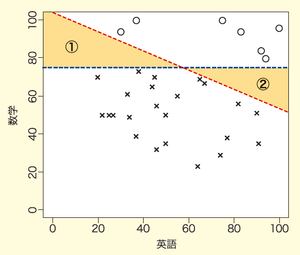
赤線で斜めに引いた境界線も,
このように新しいデータの合否判定に利用することを考えると,
つまり,
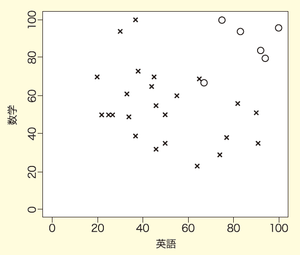
次に,
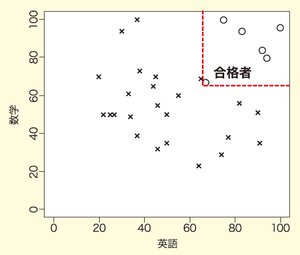
図6を見た感じでは,
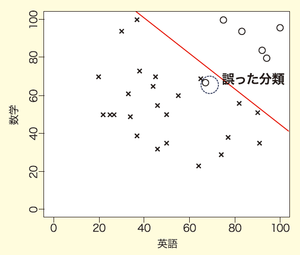
または,
合格者と不合格者を見分ける意味では,
簡単にまとめると,
もやもやする人もいるかと思いますので,
答えを知ってしまえば,
おわりに
現実には分類基準が明らかになっていない状態のデータが数多く存在します
簡単に答えが求まらないような問題に直面した時に,