宝クジの購入は非合理的
人間は確率的な思考が得意ではありません。宝クジが当たる確率は非常に低く、
宝クジの場合は嫌なら買わなければよいのですが、
間違えやすい確率問題
確率計算が必要な問題は、
誕生日一致問題
確率の見積りを間違えやすい例として、
数式による計算
誕生日が一致する2人がいる確率の計算は比較的簡単です。N人の人間の誕生日がすべて異なる確率を計算し、
p = 1 * 364/365 * 363/365 * ... (365+1-N)/365という式で計算できます。
50人いた場合に誕生日が一致する2人がいる確率
n = (ARGV.shift || 50).to_i
p = 1.0
n.times { |i|
p *= (365.0 - i) / 365.0
}
puts 1.0 - p実行結果は次のようになります。
% ruby tanjoubi0.rb 50
0.9703735750人いた場合に誕生日が一致する2人がいる確率は、
シミュレーションによる計算
数式による計算結果が心配な場合、
n = (ARGV.shift || 50).to_i # 人間の数
trials = (ARGV.shift || 10000).to_i # 試行回数
match = 0 # 同じ誕生日の人がいた回数
trials.times {
birthday = {}
n.times { |i|
day = rand(365)
if birthday[day] then # 誕生日の衝突発見
puts "#{birthday[day]}番目と#{i}番目が一致"
match += 1
break
end
birthday[day] = i
}
}
puts match.to_f / trials.to_f実行結果は次のようになります。
% ruby tanjoubi.rb 50
0番目と20番目が一致
2番目と22番目が一致
...
15番目と23番目が一致
5番目と26番目が一致
0.972850人いた場合に誕生日が一致する2人がいる確率も、
兄弟の性別問題
誕生日一致問題の場合、
「2人の子どもの一方が男の子の場合、 2人の子どもをA、 一方が男の子であるケースは3種類ありますが、 この問題の場合も、 実際に男の子/ 実行結果は次のようになります。 シミュレーションでも約33% 先の例を少し複雑にしたものとして、 実際にシミュレーションするRubyプログラムは次のようになります。 実行結果は次のようになります。 確率は1/ 確率の見積りを誰もが間違えやすい問題として、 「プレイヤーの前に3つのドアがあって、 ここでプレイヤーは最初に選んだドアを、 ── 直感的には、 この問題は非常に勘違いしやすいものであり、 この問題を忠実に再現するRubyプログラムを書くと次のようになります。 これを実行すると、 プログラムを見ると、 確率の計算をするとき、 「ランダムなもの」 完全にランダムな数値列であっても、 たとえば円周率の数字列は乱数列であるはずですが、 次のRubyプログラムを実行して200個の数字をランダムに出力します。 すると、 また、 10枚の写真をランダムにスライドショー表示しようとする場合、 N枚のスライドをランダムに再生するとき、 100枚の写真のスライドショーを行う場合、 本当にランダムなものではなくランダムっぽく感じられる値を得るためには、 このような性質を持つニセ乱数関数rand2()を用いて、 rand()の代わりにrand2()を使うと、 ランダムに感じる二次元表示を行いたい場合も、 図5の 一方、 乱数で簡単にいろいろなシミュレーションができることはわかりましたが、 最近のプログラミング言語には優秀な乱数生成ライブラリがあるのが普通です。たとえばRuby 1. 上のプログラムをSnowLeopard上で実行して生成した座標をプロットすると、 ここではrand()が小さな値を返したときだけプロットするという変な条件を付けているために目に見える形でこのような不具合が発生しています。今回の記事で紹介したような簡単なシミュレーションではこういう問題が出ることはめったにありませんが、 この問題の場合はrand()をrandom()に変更するとこのようなことは起こりません。乱数を使って複雑なシミュレーションを行う場合は注意しましょう。 連載場合分けによる計算
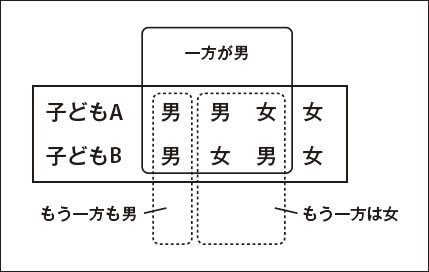
シミュレーションによる計算
trials = (ARGV.% ruby danshi.rb
BOY: 2487
GIRL: 5023
Ratio: 0.33115845539281火曜日に生まれた男の子問題
trials = (ARGV.shift || 100000).to_i # 試行回数
boys = 0; girls = 0
BOY = 0; GIRL = 1
trials.times {
# 子どもの性別と生まれた曜日をランダムにセット
gender = []
gender[0] = rand(2)
gender[1] = rand(2)
weekday = []
weekday[0] = rand(7)
weekday[1] = rand(7)
# 一方が男の子で火曜日生まれだった場合だけ計算
if (gender[0] == BOY && weekday[0] == 2) ||
(gender[1] == BOY && weekday[1] == 2) then
# 男の子のどちらかを選択してind1に格納
if (gender[0] == BOY && weekday[0] == 2) &&
(gender[1] == BOY && weekday[1] == 2) then
ind1 = rand(2)
elsif gender[0] == BOY && weekday[0] == 2 then
ind1 = 0
elsif gender[1] == BOY && weekday[1] == 2 then
ind1 = 1
end
# もう一方をind2に格納
ind2 = (ind1 == 0 ? 1 : 0)
boys += 1 if gender[ind2] == BOY
girls += 1 if gender[ind2] == GIRL
end
}
puts "BOY: #{boys}"
puts "GIRL: #{girls}"
puts "Ratio: #{boys.to_f/(boys+girls)}"% ruby kayou.rb
BOY: 6619
GIRL: 7233
Ratio: 0.477837135431707モンティ・
2011年1月24日 12:12trials = (ARGV.shift || 100000).to_i # 試行回数
fail = 0 # 当たりを引いた回数
success = 0 # ハズレを引いた回数
trials.times {
# 0、1、2の3つのドアから当たりドアをランダムに決める
# プレイヤーは0番のドアをもらう
hit = []
hit[rand(3)] = true
# モンティ・ホールの操作
# ランダムにドア1、2を開け、ハズレが出るまで繰り返す
while true do
opendoor = rand(2) + 1 # ランダムに1か2を選択
break if ! hit[opendoor]
end
print "モンティは#{opendoor}番のドアを開けました。"
if hit[0] then #
success += 1; puts "当たりです!"
else
fail += 1; puts "ハズレです!"
end
}
puts "Success: #{success}"
puts "Fail: #{fail}"
puts "Ratio: #{success.to_f/trials}"% ruby monty.rb
モンティは2番のドアを開けました。ハズレです!
モンティは2番のドアを開けました。ハズレです!
モンティは2番のドアを開けました。ハズレです!
モンティは1番のドアを開けました。当たりです!
モンティは1番のドアを開けました。ハズレです!
....
モンティは1番のドアを開けました。ハズレです!
モンティは1番のドアを開けました。当たりです!
Success: 3354
Fail: 6646
Ratio: 0.3354乱数とランダム感
ランダムなのにランダムではなく感じる
円周率
3.1415926535897932384626ランダムな数字
200.times {
print rand(10)
}5537341995738855180096821833451569453844512654843598428
0087032949714244066204568524660685406218469646838262876
9542110440797093575480604480484163727741078660949341570
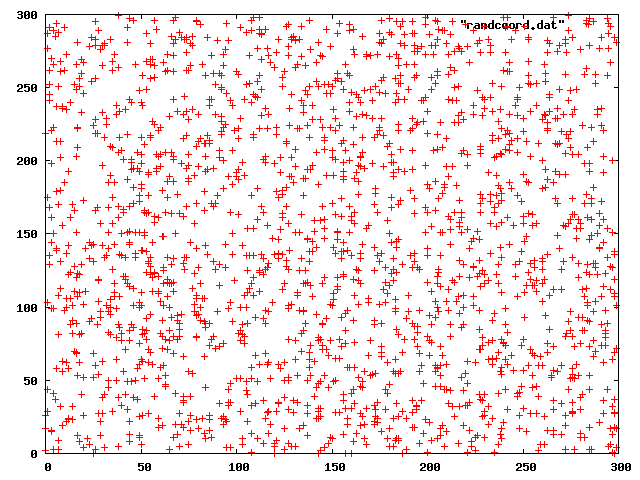
92911640557823043091823428633318910ランダムな二次元座標
1000.times {
puts "#{rand(256)} #{rand(256)}"
}
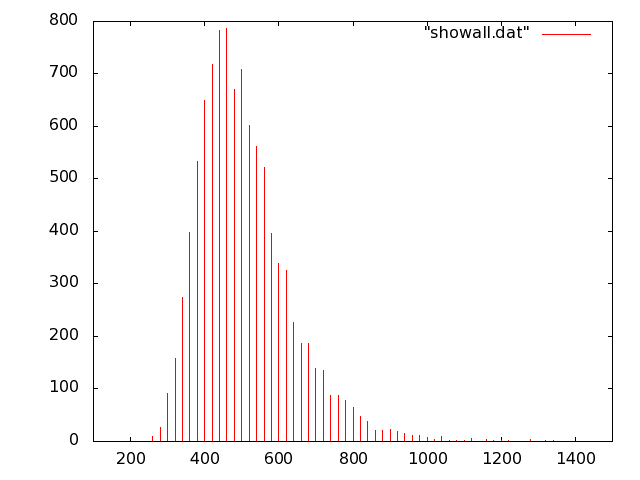
ランダムなスライドショー
n = (ARGV.shift || 100).to_i # スライドの数
trials = (ARGV.shift || 10000).to_i # 試行回数
histdiv = (ARGV.shift || 20).to_i # ヒストグラムの粒度
lim = (ARGV.shift || 2000).to_i # 表示上限
hist = [] # ヒストグラム
trials.times {
shown = []
nshown = 0
count = 0
while nshown < n do
ind = rand(n)
if !shown[ind] then
shown[ind] = true
nshown += 1
end
count += 1
end
hist[count/histdiv] = hist[count/histdiv].to_i + 1
}
100000.times { |i|
puts "#{i*histdiv} #{hist[i].to_i}"
break if i*histdiv >= lim
}
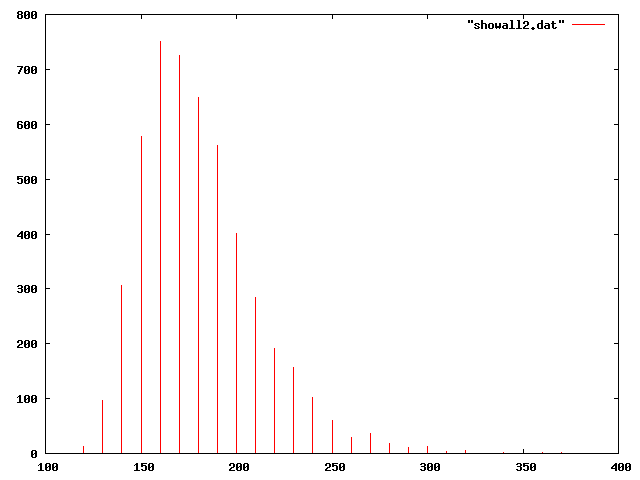
ニセ乱数
n = (ARGV.shift || 100).to_i # スライドの数
trials = (ARGV.shift || 10000).to_i # 試行回数
histdiv = (ARGV.shift || 10).to_i # ヒストグラムの粒度
lim = (ARGV.shift || 1000).to_i # 表示上限
hist = [] # ヒストグラム
$randhist = [] # ニセ乱数の過去値リスト
def rand2(n)
# 出やすさを決めてprob[]に格納
prob = []
$randhist.each { |val|
prob[val] = 1
}
# 特に最近出たものは外す
recentlen = 3
recentlen = n-1 if recentlen >= n
(1..recentlen).each { |i|
break if $randhist[-i].nil?
prob[$randhist[-i]] = 0
}
# 出ていないもの優先で割り当て
(0...n).each { |i|
if !prob[i] then
prob[i] = 10 # 10倍出やすくする
end
}
# prob[] に基づいてニセ乱数を計算
a = []
(0...n).each { |i|
prob[i].times {
a.push(i)
}
}
v = a[rand(a.length)]
# ヒストリ保存
$randhist.shift if $randhist.length >= n
$randhist.push(v)
return v
end
trials.times {
shown = []
nshown = 0
count = 0
while nshown < n do
ind = rand2(n)
if !shown[ind] then
shown[ind] = true
nshown += 1
end
count += 1
end
hist[count/histdiv] = hist[count/histdiv].to_i + 1
}
100000.times { |i|
puts "#{i*histdiv} #{hist[i].to_i}"
break if i*histdiv >= lim
}
二次元ニセ乱数


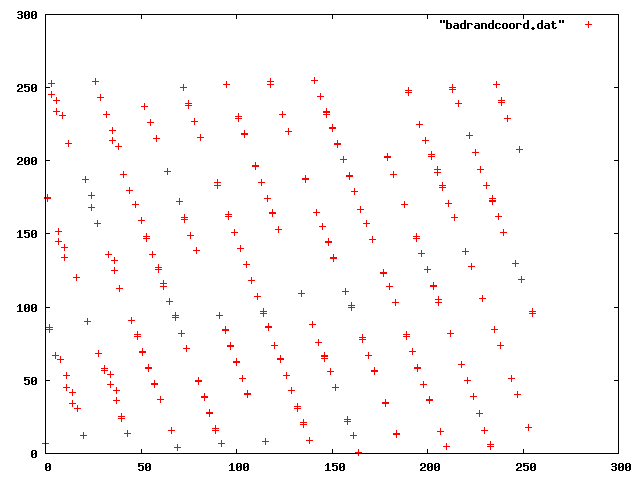
乱数の精度
#include
main()
{
for(;;){
int x = rand();
int y = rand();
if(x < 0x100000 && y < 0x100000){
printf("%d %d\n",x & 0xff,y & 0xff);
}
}
}
連載のおわりに



