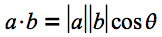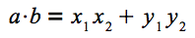はじめに
今回は臨時回として、第2回 で取り上げた線分の交差判定について再度考えます。第2回の実装には、ある特別な状況下で正しく動作しないという問題がありました(筆者が執筆時点で問題を見落としていました。申し訳ありません) 。
この問題を解決するために、前回学んだばかりのCCW関数を活用し、線分の交差判定を別のアプローチから実装することができます。ちょうど良い機会ですので、今回はその再実装を行ってみたいと思います。
何が問題なのか
第2回では、線分の交差判定を行うLineSegment#intersects()メソッドを以下のように作成しました。
リスト LineSegment#intersects()メソッド(Java) public boolean intersects(LineSegment s) {
return intersects(s.toLine()) && s.intersects(toLine());
}これは、線分を延長して直線化し、直線と線分の交差問題に置き換えるという方針に基づく実装です。しかし、図1 のように2つの線分が一直線上に並ぶ場合、上のコードは常にtrueを返してしまいます。
図1 一直線上に並ぶ2線分本来、一直線上に並ぶ2線分に対しては、図2 のように、線分が共有部分を持つときのみ交差としなければなりません。第2回のintersects()メソッドには、こうした問題があったのです。
図2 一直線上で共有部分を持つ2線分ところで、前回取り上げたCCW関数のアプローチを使い、上記の問題を回避できる線分の交差判定の方法が存在します。そこで今回は、CCW関数を使ってLineSegment#intersects()メソッドを書き直してみることにします。
CCW関数による交差判定
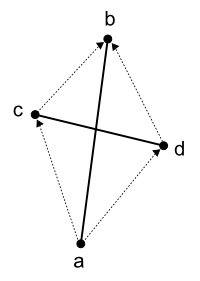
図3 のように、線分abとcdがあるとします。ここで、aからスタートし、cまたはdを経由してbまで進む経路、a→c→bとa→d→bの2つを考えます。
図3 2つの経路もし、abとcdが交差するのであれば、cとdはabを挟んで互いに向き合うかたちになりますから、a→c→bとa→d→bのCCW値は符号が異なるか、少なくとも一方がゼロになるはずです。CCW値が両方とも正または負になることはあり得ません。
さらに、同じ条件が、cからスタートし、aまたはbを経由してdまで進む経路、c→a→dとc→b→dについてもみたされる必要があります。
したがって、これら4つのCCW値であるccw(a, c, b), ccw(a, d, b), ccw(c, a, d), ccw(c, b, d)の符号を調べれば、線分の交差判定ができることになります。
さて、線分が図1や図2のように一直線上に存在する場合、これらのCCW値はすべてゼロになります。このときに限り、abとcdが図2のように共有部分を持つかどうかを調べる追加処理が必要です。この共有部分を持つ条件は、cまたはdがaとbの内分点になっているか、aまたはbがcとdの内分点になっているときに成立します。
では、点が線分を内分しているかどうかを判定するには、どうすれば良いのでしょうか。それには、ベクトルの内積が利用できます。
ベクトルの内積
ベクトルの内積は、以下の式で定義されます。
式1 ベクトルの内積また、ベクトルaを(x1 , y1 )、ベクトルbを(x2 , y2 )と成分表示すると、aとbの内積は以下の式で計算できます。
式2 ベクトルの成分による内積の計算式ここでまず、前回作成したGeomUtilsクラスに、この内積の計算を行うdot()メソッドを追加しておきましょう。dotという名前は、ベクトルの内積がドット積とも呼ばれることに由来します。
リスト 内積の計算(Java) public static double dot(double x1, double y1, double x2, double y2) {
return x1 * x2 + y1 * y2;
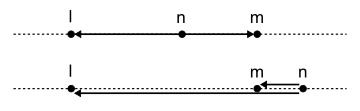
}さて、図4 を見てください。点l, m, nに関して、ベクトルnlとnmを考えます。nがlmを内分する場合、nlとnmは互いに逆方向を向くので、nlとnmのなす角度θは180度となり、cosθが-1となるので、その内積は負の値になります。一方、nがlmを外分する場合、nlとnmの向きは一致するのでθは0度となり、cosθが1となるので、内積は正の値になります。また、nがlまたはmに重なる場合は、ベクトルnlまたはnmの大きさがゼロになるので、内積もゼロになります。
図4 内分点・外分点とベクトルの向き このように、内積の符号を見ることで、点が線分の内部と外部のどちらに存在するかが分かります。ここから、一直線上に並ぶ2つの線分が共有部分を持つかどうかを判定できるのです。
交差判定の再実装
ここまで見てきた内容をすべてふまえて、LineSegmentクラスのintersects()メソッドを書き直すと、以下のようなコードになります。
書き直したintersects()メソッド(Java)
// 第7回で書き直し
public boolean intersects(LineSegment s) {
return bothSides(s) && s.bothSides(this);
}
// sが自線分の「両側」にあるかどうかを調べる
private boolean bothSides(LineSegment s) {
double ccw1 = GeomUtils.ccw(x1, y1, s.x1, s.y1, x2, y2);
double ccw2 = GeomUtils.ccw(x1, y1, s.x2, s.y2, x2, y2);
if (ccw1 == 0 && ccw2 == 0) { // sと自線分が一直線上にある場合
// sのいずれか1つの端点が自線分を内分していれば、sは自線分と共有部分を持つので
// trueを返す
return internal(s.x1, s.y1) || internal(s.x2, s.y2);
} else { // それ以外の場合
// CCW値の符号が異なる場合にtrueを返す
return ccw1 * ccw2 動作確認
デモプログラムを作成して、新しいintersects()メソッドの動作を確認してみます。
リスト デモプログラム(Java) public class RevisedLineSegmentDemo {
public static void main(String[] args) {
LineSegment s1 = new LineSegment(0, 0, 100, 0);
LineSegment s2 = new LineSegment(99, 0, 200, 0);
LineSegment s3 = new LineSegment(101, 0, 200, 0);
System.out.println(s1.intersects(s2));
System.out.println(s1.intersects(s3));
}
}このプログラムで、s1, s2, s3は同一の直線上に存在します。s1とs2は一部重なっていますが、s1とs3は離れています。プログラムを実行すると、以下の出力が得られます。
図 デモプログラムの実行結果true
falseintersects()メソッドを書き直したことにより、一直線上に並ぶ線分に対しても、正しく交差を判定できていることがわかります。
まとめと次回予告
今回は、第2回で実装した線分の交差判定に問題があることを説明し、CCW関数とベクトルの内積を使った新しい実装を行いました。図らずも、CCW関数の有用性を示す回になったと言えるかもしれません。
今回作成したプログラムのソースコードがダウンロードできます。
次回は、当初予定していた多角形の話題に戻りたいと思います。お楽しみに!