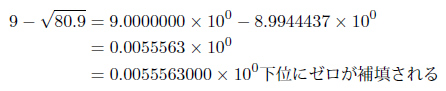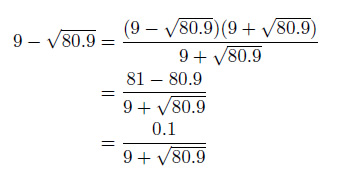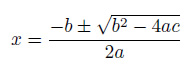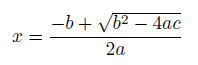コンピュータで実数を表現するために工夫された浮動小数点数は、仮数部分を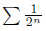 で近似する方法です。
で近似する方法です。
取り扱える数の範囲や精度は、指数部と仮数部の桁数によって決まります。このしくみは自由に伸び縮みさせることができる伸縮性の物差しに例えることができます。大変便利なのですが、コンピュータの物差しは目盛りに無い数値は取り扱うことができません。数値が目盛りと目盛りの間に存在する場合は、何らかの約束事に従って、どちらかの目盛りを読み取ります。このようにして読み取った値は近似値といい、真の値との間に誤差があります。
コンピュータで計算を行う人は、このことをよく知っておきましょう。コンピュータは万能ではありません。大変便利な機械ですが、より大きな利便を得るためにちょっとした妥協をしています。時によってはこの妥協が大きな計算違いを生むことがあるのです。プロとしてコンピュータを用いるならば、この妥協による誤差がどんなもので、どの程度の誤差を発生するのかを必要とあらば把握できなければなりません。
コンピュータの数値の取り扱い方法のしくみを知り、誤差を把握することは、ちょうど大工さんが自分の道具に精通するのと似ています。
これから数回にわたって、コンピュータで実数値を取り扱うときに生じるエラーや誤差について学びます。将来本格的な数値計算を行う場合に役立つ知識です。コンピュータで数学的な問題を取り扱うことに興味を持たれている読者の皆さんは、このチャンスに浮動小数点数の弱点をしっかりと知りましょう。
図10.1 名人は道具をきわめる

浮動小数点数で発生するエラーや誤差
浮動小数点数の仕組み上、避けられないエラーや誤差には以下に挙げるものがあります。
- オーバーフロー/アンダーフロー
- 桁落ち
- 丸め誤差
- 情報欠落
- 打ち切り誤差
今回はこれらのうち「オーバーフロー/アンダーフロー」と「桁落ち」を学習しましょう。
オーバーフロー/アンダーフロー
オーバーフロー/アンダーフローとは、算術演算の結果、絶対値が表現可能な範囲を超えることを意味します。
オーバーフローが発生すると、Java言語の実数型では無限大(Infinity)と表現されます。アンダーフローが発生すると、Java言語の実数型では0として取り扱います。Java言語ではどちらの場合もエラーとしては取り扱いません。
具体的にはIEEE754単精度(float型)の場合[1]、指数部が最大値の254を超えた場合がオーバーフローになります。float型は指数部255、符号部、仮数部ともに0で正の無限大を表します。符号部が1の場合は負の無限大です。指数部が最小値の0を下回る場合はアンダーフローです。その実数型の値は単に0になります。
オーバーフローもアンダーフローも、真の値は無限大やゼロではないにもかかわらず計算に支障が出る状況です。ものの寸法や個数などを扱う場合に、float型やdouble型の最大値は十分大きいように思われますが、各種計算式の途中で大変大きな数を生じる関数を用いている場合などはオーバーフローに注意が必要です。大きな数値の逆数が生じる場合も、その値がアンダーフローするとゼロ扱いになってしまいます。科学技術計算を行うプログラムを書く場合には、当然のことですが想定できる範囲のテストデータを用いて、計算途中の値をチェックしましょう。
桁落ち
桁落ちとは、値が大変近い浮動小数点数の減算の結果、有効数字[2]の桁数が減少してしまうことです。
IEEE754単精度では仮数部が10進数にして約8桁、倍精度でも約15桁の桁数しか表現できません。桁落ちにより簡単にとんでもない計算結果になる可能性があります。近接する値の減算を繰り返し行う場合には、十分検討が必要です。桁落ちを避けるためには、式変形により減算を加算に変形する方法があります。
値が大変近い数値の減算例として、次の式を見てみましょう。
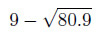
9の二乗の81にわずかに満たない数値の平方根は、9に大変近い数値になるでしょう。それぞれの数値を今回はfloat型に格納して計算してみましょう[3]。float型は10進数にして仮数部が8桁程度です。最も下位の桁には丸めが入っていますから数値として正確であることが期待できるのは7桁程度です。つまり、今回の計算は有効数字7桁の計算であるといえます。計算をする人は計算結果に有効数字7桁が保証されることを期待します。
さて、この計算をJava言語で次のように計算させてみましょう。
float a = 9;
float b = (float) Math.sqrt(80.9);
float c = a - b;
なんの変哲もありません。ただ引き算をしただけです。しかしこの計算の結果は0.0055570602になります。試しにWindowsの電卓を用いて計算してみると0.0055572712924565534295443750356158という値が得られます。こちらが正しいとすると、一致する桁はたったの4桁しかありません。桁落ちが発生したのです。これは困ったことです。たった一度の減算を行っただけで、精度がこんなに落ちてしまいました。
この現象は次のように説明できます。float型に数値を格納すると、数値は仮数部と指数部に分けられます。仮数部には表現可能な桁数に限界があり、それが10進数にしておよそ8桁です。最大で8桁の有効数字であるといえます。8桁の有効数字を持つfloat型で、今回の計算は次のように行われます。浮動小数点数の加減算は指数部を同じ値にそろえ、仮数部のみの演算を行います。
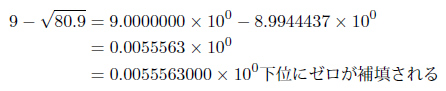
浮動小数点数は、この計算結果を有効数字8桁分で保持します。更に、計算結果の有効数字が減った分をゼロで補い、その値の近似値を保持しますから、計算結果の有効数字4桁目か5桁目からは真の値からずれていきます。
浮動小数点数の減算は、このような問題点を持っています。桁落ちを回避するためには、近接する値の減算が予想される場合に減算を用いない計算方法をしなければなりません。
例えば次のように式を変形することで回避できます。
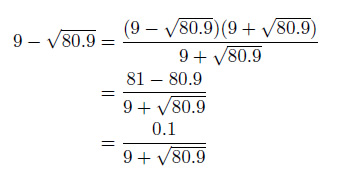
このように式を変形してJava言語で計算すると0.0055572717という結果が得られました。先ほどの電卓の計算結果と比較すると、7桁一致しました。4桁だった精度が7桁まで回復しています。
同様の計算でよく問題になるのは、二次方程式の解の公式です。
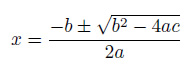
bの値が正で、4acの値が非常に小さい場合、次の式の分子の計算で桁落ちの発生する危険性があります。
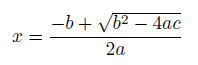
この式での桁落ちを回避するためにどのように式変形できるでしょうか。これを今回の演習としましょう。
今回はここまで
数式が多くなりましたが避けて通れない関門です。しっかり手と頭を使ってクリアしましょう。
![]() で近似する方法です。
で近似する方法です。
![]()