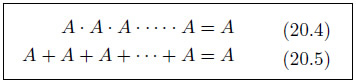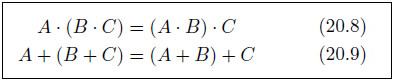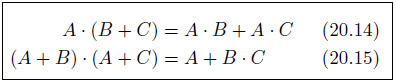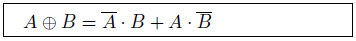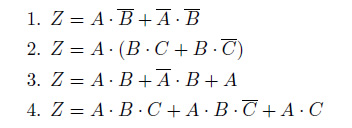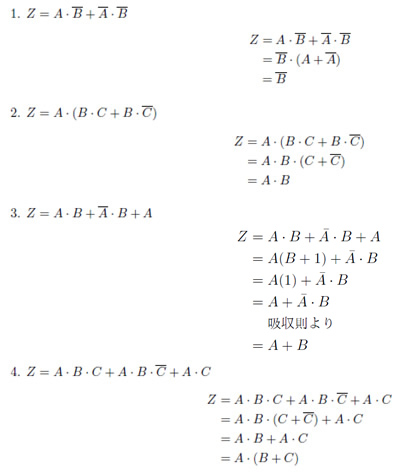今回も論理代数の定理・公式を紹介していきます。それぞれの公式について真理値表をつくることで、公式の働きを感覚的に納得しましょう。最後に計算問題を用意していますので、使い方に慣れましょう。
論理代数の定理・公式のつづき
補元則

補元則はその演算結果が真か偽になりますから、零元則や単位元則とともに働いて式が劇的に簡略化される場合があります。忘れずに適用したいルールです。
式20.1は次のように値を当てはめると分かりやすいでしょう。仮にAが真ならば、Aは偽です。常に裏返しのものの論理積をとれば、どちらかが必ず偽なのですから全体として真になりようがありません。ですから結果は常に偽です。
式20.2も同様に考えると分かりやすくなります。常に裏返しのもの同士の論理和は、どちらかが必ず真なのですから全体として常に真になります。
対合則

対合則はいかめしい名前ですが、要は「裏の裏は表」ということです。復元の定理とも呼ばれます。
べき等則
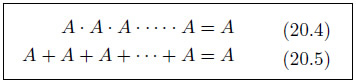
同じものに関して何度論理和や論理積をとっても同じだと宣言しています。具体的な事柄で表現すると、吹き出しそうな文章になりますがしっくり納得できます。せっかくだからやってみましょう。Aが「明日は晴れ」を表すとします。すると、式20.4の左辺は、『「明日は晴れ」かつ「明日は晴れ」かつ…かつ「明日は晴れ」です』。どう転んでも、明日が雨になりそうになりませんね。
交換則

交換則は2つの論理値の論理演算の順番を入れ替えても結果に差がないことを表しています。
結合則
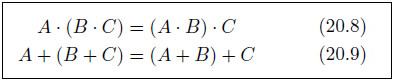
結合則も交換則同様、シンプルで理解しやすいものです。同じ論理演算子で結ばれた論理変数は、括弧でくくる位置を自由に変更できます。
吸収則

さて、論理代数の公式はここからが大事なところです。直感的にはすぐに納得しかねる式が出てきます。一番良いのは地道に真理値表を作成し、左辺と右辺が等しくなることを確かめて納得することです。では、式20.10について試してみましょう。
表20.1 式20.10の真理値表
| A | B | A+B | (A+B)・A |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
真理値表から、Aと(A+B)・Aの列が確かに同じことがわかります。
吸収則はその名の通り式中の論理変数が吸収されて姿を消してしまいます。式の簡略化に役立つ公式です。
分配則
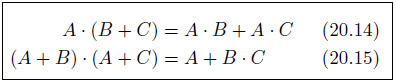
式20.14は一般的な代数の公式と同形ですから納得しやすいでしょう。しかし、式20.15はちょっと異なりますね。どう考えればよいでしょうか。先ず、A・Aはべき等則によりAになることが理解できます。では、B・Aはどこへ消えたのでしょうか。先ずは交換則の式20.6から、B・A=A・Bです。吸収則の式20.11を思い出してください。A+A・B=Aでしたね。こうして式20.15が導かれました。
ド・モルガンの定理

ド・モルガンの定理は論理積を論理和に、論理和を論理積に変換したいときに活用します。式をすっきり納得するには、真理値表を作るのがよいでしょう。確かに左辺と右辺を表す列が一致します。
排他的論理和
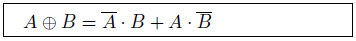
最後に排他的論理和を紹介します。右辺のような形の論理式が表れたら、排他的論理和の記号で短くシンプルな式に変換できます。また、式中の排他的論理和の部分を展開して、更に式の整理が出来る場合もあるでしょう。場合に応じて活用できるようにしておきましょう。
問題:次の論理式を論理代数の公式を使って簡略化しましょう。
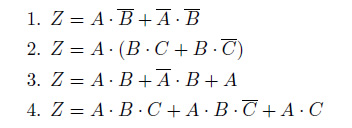
解説
それぞれの式を、公式を用いて整理した様子を示します。
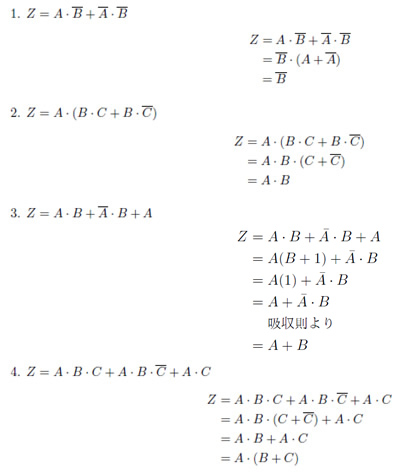
今回はここまで
いかがでしたか?たくさんの公式に圧倒されましたか?しかし、ひとつひとつは大変シンプルです。公式は道具です。知っているだけでは使えません。道具は使ってこそ身に付きます。全ての問題を公式と照らし合わせながら解いて下さい。そうすれば必ずこのスキルが身につきます。次回は文章の形の命題から論理式を作る練習をしましょう。