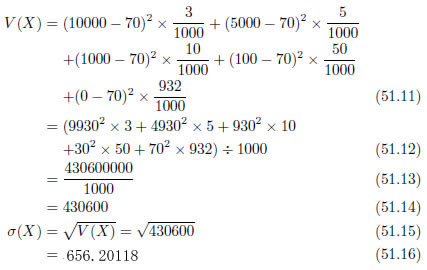勝負事の世界では、一発狙いの勝負師もいれば、堅実に小さな勝ちを積み重ねていくタイプの勝負師もいます。柔道の世界に例えれば、一発狙いは大技で派手に勝ちたいタイプ。有効以上のポイントを積み重ね、あとは守りに徹し、チャンスがあれば合わせ技一本を狙うのが堅実なタイプでしょう。もちろん、伝統的な柔道では一発の技を美しく決めることが推奨されますが、団体戦で格上の相手と当たり、何が何でも引き分け以上、負けられない試合では、見た目にはみっともない戦い方もやむを得ないことがあります。確率の数学で言うところの、引き分け以上の確率が最も大きいような戦い方をするのです。
今回学習するのは、そのような確率の活用に役立つ、期待値・分散・標準偏差といった、確率をより実際的に用いるための道具だてを紹介します。
図52.1 何が何でも引き分け以上を

期待値
期待値[1]とは、各事象の値、すなわち確率変数の値に確率を乗じて合計した値のことです。期待値は事象の値の平均値ですから、単に平均値[2]と呼ぶこともあるのですが、単純な平均値と区別するために期待値と呼ぶほうが良いでしょう。期待値という言葉に主観的なニュアンスを感じますが、実際にはあくまで平均です。期待値E(X)は、次式51.1のように定義されます。
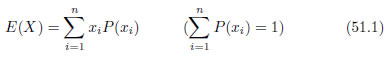
式51.1の各変数の意味は次の通りです。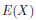 は確率変数の値の集合
は確率変数の値の集合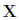 の期待値、
の期待値、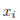 は確率変数のi番目(i個目)の値、
は確率変数のi番目(i個目)の値、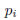 は
は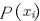 に対応する確率の値です。
に対応する確率の値です。
具体的な例を見てみましょう。
1枚100円のくじ1000本の中に、1等10000円の当たり3本、2等5000円の当たり5本、3等1000円の当たり10本、4等100円の当たり50本があるとします。残りの売上金は寄付するものとして町内会のくじが企画されました。このくじに参加した人は、平均していくらの獲得賞金が期待できるでしょうか。
均等に当選金額を分配したとして、いくら得られるかを計算しても意味がないでしょうか?とんでもありません。くじに当たる確率を高くしようと思えば、たくさんくじを買えばよいのです。そして、たくさんくじを買えば、例え外れても、均等に当選金額を分配した値に近い額を得られるかもしれないではありませんか。お金に物を言わせて、全てのくじを買い占めれば、そうなるわけですから。ですから、計算する平均値は、たくさんくじを買ったときに、一枚当たりいくらの当選金額を得られるかの予測値になります。
では計算してみましょう。
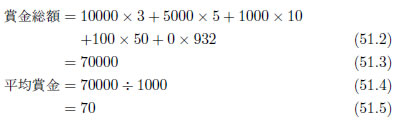
くじの胴元が寄付をすることを前提にしているわけですから、全て買ったところで得をすることは無いのが最初からわかっています。しかし、もし、賞金を均等に分配したら、と考えると、今回のくじの場合は平均して70円は返ってくる「かもしれない」ことが、今回の計算でわかりました。これを割がよいと見るか、悪いと見るかは人それぞれ。しかし、世間一般の宝くじの平均賞金が購入金額の半分以下であることを考えると、相当に割の良いくじであると思われます。
さて、これを確率の数学を用いて計算し直してみます。
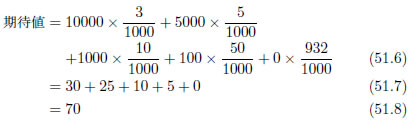
式51.5と51.8は一致しました。式をよく見てみると、実は同じことを違う形で行っているだけなのですから、一致して当たり前です。しかしながら、ある事象の値に確率の値を掛けることで、ものごとの判断材料を得ることが出来るという仕組みは大変面白いですし、有効ですね。
分散・標準偏差
試行の結果がどの程度ばらついているのかを示す指標が分散[3]です。別の言葉で言い換えれば、確率変数の分布の様子を数値で表したものです。分散は式51.9に示すように、「試行結果と期待値の差の2乗」の期待値です。「観測結果と平均値の差の2乗」の平均値と言い換えることも出来ます。2乗することで、平均値との差の正負を無視できます。分散の値が大きいと言うことは、期待値に対して大きく外れた試行結果が多く存在するということです。逆に、分散の値が小さいと言うことは、試行結果のほとんどが期待値に近いということになります。
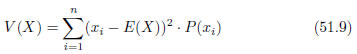
試行結果のばらつき具合を表す分散ですが、2乗値ですから具体的な適用の際「平方根はいくらだろう?」と、ちょっと考えてしまいます。そこで、分散の平方根を取ったのが標準偏差[4]σ[5]です。

こうして平方根をとっておくと、データの分散具合がイメージしやすくなります。
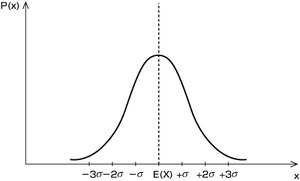
確率分布が、図52.2のように期待値を中心に山形ならば、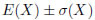 の範囲に66%のデータが入っています。
の範囲に66%のデータが入っています。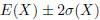 の範囲には95%、
の範囲には95%、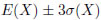 の範囲には実に99%です。「データの分布がきれいな山形ならば、
の範囲には実に99%です。「データの分布がきれいな山形ならば、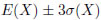 の範囲を外れるデータは大変珍しい」と表現できます。これはデータのばらつきを数値で表現したい場合に強力な道具になります。
の範囲を外れるデータは大変珍しい」と表現できます。これはデータのばらつきを数値で表現したい場合に強力な道具になります。
図52.2 ほぼ山形の確率分布の例
では、具体的な計算を行ってみましょう。期待値のところで用いたくじの場合で分散と標準偏差を計算してみます[6]。
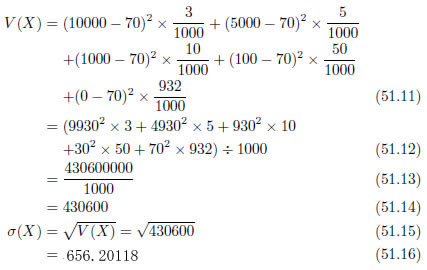
手順を眺めてみるとわかりますが、このような計算はコンピュータにさせるに限ります。シミュレーションばかりでなく、数学的に分散や標準偏差の値を求める場合はコンピュータが欠かせません。
確率と統計
今回学習した内容のうち、分散と標準偏差は統計[7]の数学の範囲になります。確率がまだ起こっていない事柄について予測するための道具だとすると、統計は既に起こった事柄について整理するための道具だと言えます。現実世界の事柄に適用していく際、確率と統計は両輪となって機能します。
今回はここまで
今回は、期待値・分散・標準偏差を紹介しました。これらは確率の数学を利用して、現在手元にあるデータを数量的に判定する道具です。言葉は難しそうに見えますが、要は平均値であったり、ばらつきの度合いのことです。言葉の堅苦しさにとらわれず、便利な道具を得たのだと思ってください。次回は実際の問題に当たってみましょう。数学的に解き、また同じ問題をJava言語でシミュレーションするプログラムを作り、統計的に解くのです。お楽しみに。

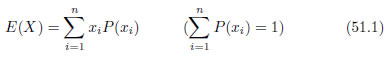
![]() は確率変数の値の集合
は確率変数の値の集合![]() の期待値、
の期待値、![]() は確率変数のi番目
は確率変数のi番目![]() は
は![]() に対応する確率の値です。
に対応する確率の値です。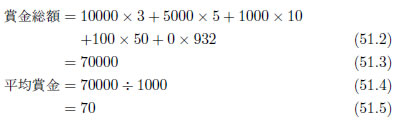
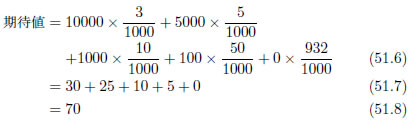
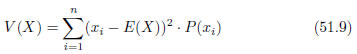

![]() の範囲に66%のデータが入っています。
の範囲に66%のデータが入っています。![]() の範囲には95%、
の範囲には95%、![]() の範囲には実に99%です。
の範囲には実に99%です。![]() の範囲を外れるデータは大変珍しい」
の範囲を外れるデータは大変珍しい」