前回は相関係数とは何か、大変大雑把に紹介し、計算手順をJava言語で実装、テストするところまで行いました。今回は、相関係数というものがどういう筋道で導かれたものなのか、丁寧に追っていきます。途中の数式を極力省かずにたどります。全て高校数学までの内容です。
今回、そして次回の前後編は、まるっきり数学ばかりです。”Javaでコンピュータ数学”の看板に偽りあり?とおっしゃらず、だまされたと思って取り組んでみてください。プログラミングを専門としていれば、少なからず「効率の良い計算」を必要とする場面があります。すると、そのときに使う数学は、ちょうど今回出てくるような「合計」や「平均」と似た操作を上手に組み合わせることが多いのです。コンピュータは「単純なんだけれども、人の手と頭ではとても処理できないような、たくさんのデータを処理すること」が最も得意な機械だからです。
これから出てくる、「数式のこねくり回し」は、最終的に「シンプルな計算」で「意味のある数値」を得るための先人の工夫の1つです。一度しっかり頭を悩ませておけば、きっと将来役にたちます。
ただ読むだけでは「わかった」気になりません。ペンと紙を用意し、単純に写すのではなく是非とも頭を使って考えましょう。それが理解の最短コースです。
相関係数を導く
目的 回帰直線が測定値に良くあてはまっているかを知りたい
連載第59回では、微分方程式を用いて解析的に最小二乗法で回帰直線の定数を求めました。今回は、統計の数学を用いて、最小二乗法で回帰直線の定数を求め、その定数が良くあてはまっているかを確認する材料となる相関係数の値を得るための式を導きます。相関係数は、回帰直線が測定値に良くあてはまっているかを知りたいから定義された、と言い直しても良いでしょう。
それでは、旅の始まりです。
準備 分散の計算方法
分散は、測定値の分散具合を表す目安です。旅の途中で必要となりますので、ここで計算方法をおさらいしておきます。
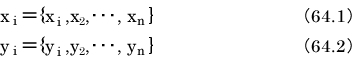
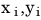 はある事象の測定値です。場合によっては観測値とも呼びます[1]。
はある事象の測定値です。場合によっては観測値とも呼びます[1]。
平均値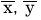 は次の通りです。それぞれ「エックス・バー」、「ワイ・バー」と読みます。
は次の通りです。それぞれ「エックス・バー」、「ワイ・バー」と読みます。

測定値x,yのばらつき具合を表すために、以下の3つの式で分散を定義します。
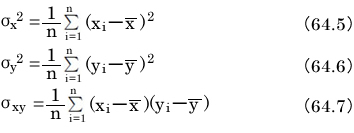
ここで、xの分散(式64.5)、yの分散(式64.6)は二乗の値ですから必ず0以上の正の値であることと、xとyの共分散(式64.7)は正負の値を取り得るところを記憶にとどめておいてください。σはギリシャ文字で「シグマ」と読みます。
最小二乗法で回帰直線を求める
2つの変数(ここではxとy)の間に、直線の関係式(一次式)が成り立つと仮定されるとき、その直線のことを回帰直線といいます。その直線の定数を求めたいのですが、どのように求めればよいのでしょうか。
無数に考えられる定数の中から決定する方法として最小二乗法があります。
図64.1 最小二乗法
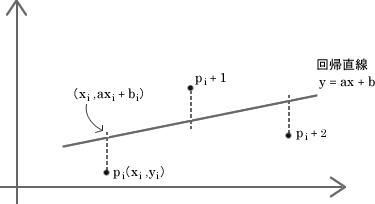
図64.1に、グラフ上にプロットしたデータp i からp i+2 に対して回帰直線(y=ax+b)を引いたところを示します。
最小二乗法とは、図64.1の中のd i の2乗の合計が、最小になるように定数aとbを決める方法です。
d i のことを誤差[2]と呼ぶことにしましょう。p i の座標値が測定値です。
これに対してx i に対応した回帰直線上のy座標値(ax i+b )を推定値[3]と呼ぶことにします。記号は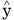 で「ワイハット」と読みます。
で「ワイハット」と読みます。
誤差の合計を最小にする
誤差の合計を最小にしたいのですが、単純にd i =y i -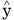 とし、d i の合計を取ると都合が悪いことになります。推定値に対して測定値は大きいこともあれば小さいこともあります。つまり、diは正も負もあるので、単純合計では相殺されてしまう部分があるのです。大きくばらついていても、回帰直線が上手いことデータのばらつきの中心を横切った場合に、合計がゼロに近い値となることが想像できます。
とし、d i の合計を取ると都合が悪いことになります。推定値に対して測定値は大きいこともあれば小さいこともあります。つまり、diは正も負もあるので、単純合計では相殺されてしまう部分があるのです。大きくばらついていても、回帰直線が上手いことデータのばらつきの中心を横切った場合に、合計がゼロに近い値となることが想像できます。
そこで誤差の2乗の合計を取るのです。
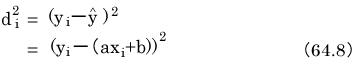
以後、分散や平均という形で各項を書きたいので、そうなるように式変形していきます。
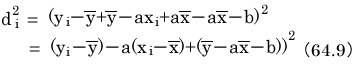
このまま展開しても良いのですが、大変手間ですので、次のように読みかえます。
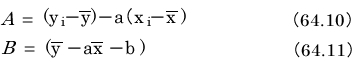
この読みかえで、式は次のように簡単になります。
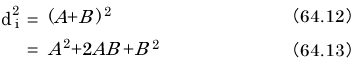
ここで、それぞれの項について計算します。
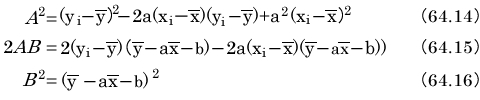
式64.14の各項は上手い具合に分散と共分散で表現できそうです。式64.16は定数値です。残るは式64.15です。これはどう処理できるでしょうか。
式64.15をi=1・・・nで合計してみましょう。このような手順を取るのは、うまくいけば、合計の結果をnで割ると分散の形で表現できるからです。
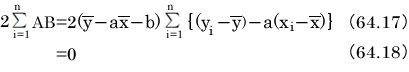
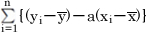 は、平均値と測定値の差の合計です。これは意味から考えて、ゼロになります。
は、平均値と測定値の差の合計です。これは意味から考えて、ゼロになります。
以上のことから、式64.15は、式変形を待つまでもなく消えました。
式64.12について、i=1…nで合計し平均をとりましょう。そうすると各項が分散の形で表されるからです。
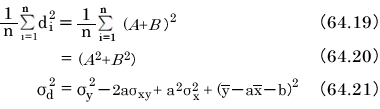
この式から、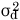 が最小となるときの、定数aとbの値を求めたいのです。そして、定数aとbは分散や共分散で表現したいのです。式64.21はaについて2次の式です。係数は
が最小となるときの、定数aとbの値を求めたいのです。そして、定数aとbは分散や共分散で表現したいのです。式64.21はaについて2次の式です。係数は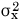 ですから正、よって下に凸のグラフとなります。極小となるときのaの値を代数的に導きましょう。
ですから正、よって下に凸のグラフとなります。極小となるときのaの値を代数的に導きましょう。
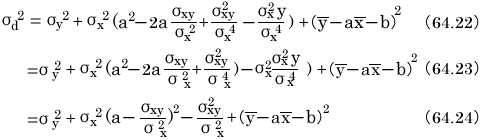
式64.24をa中心に並べると、次の式になる。
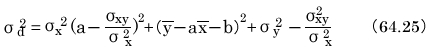
式64.25が最小となるのは、次の場合であることがわかります。

式63.26と63.27より、

こうして、測定値の集合に対する回帰直線の定数aとbを決定する式を得ることが出来ました。
以上の結果を用いて、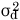 が最も小さいときの値として次の式を得ることが出来ます。
が最も小さいときの値として次の式を得ることが出来ます。

今回はここまで
統計の数学を用いて最小二乗法によって得られる回帰直線の定数a,bを導きました。さて、次回はいよいよ、測定データと回帰直線の間の関係の強さを判定します。次回までに、今回演繹したところを、自分で導出できるようにしてみませんか。例えば、式64.9から64.21の間です。この辺をごりごりと書き下せるようになると、計算処理の簡略化の必要な課題で力を発揮できるようになるでしょう。
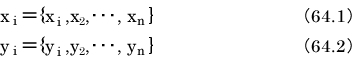
![]() はある事象の測定値です。場合によっては観測値とも呼びます
はある事象の測定値です。場合によっては観測値とも呼びます![]() は次の通りです。それぞれ
は次の通りです。それぞれ
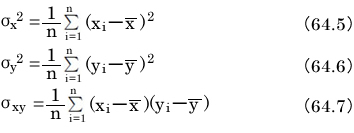

![]() で
で![]() とし、
とし、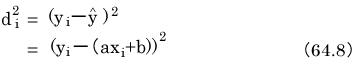
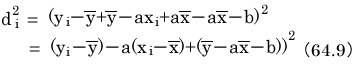
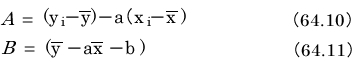
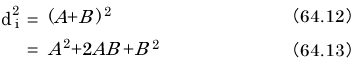
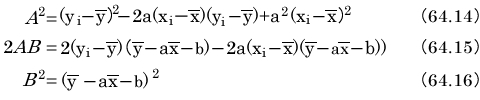
![]()
![]() は、
は、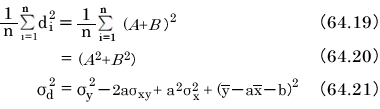
![]() が最小となるときの、
が最小となるときの、![]() ですから正、
ですから正、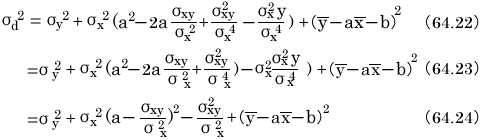
![]()


![]() が最も小さいときの値として次の式を得ることが出来ます。
が最も小さいときの値として次の式を得ることが出来ます。



