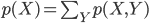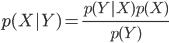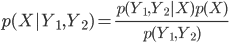今回は、機械学習で使う「確率」のお話です。
確率は、統計的な機械学習のもっとも重要な基礎知識です。とはいえ、確率についてゼロから説明するというのは紙数的にも厳しいため、高校の確率を少し憶えているくらい(期待値や標準偏差など)を前提とし、「 高校の確率」と「機械学習の確率」の本質的な相違点について、少し丁寧に見ていく、という形で進めていきます。
機械学習と確率
最初に、機械学習にとって確率はどういう役割なのかを確認しておきましょう。
実のところ、機械学習に確率が必須というわけではありません。ニューラルネットワークやサポートベクターマシンなどの有名な手法も「確率を用いない機械学習」ですし、その他にも数多くの手法があります。しかし、「 確率を用いない機械学習」の多くは、「 結果のランキングを作りづらい(評価値の大小に意味がない) 」 「 条件が異なる場合の結果を比較できない」などの欠点があります。
一方の「確率を用いる機械学習」では、評価結果や推定されたパラメータが「どれくらい信用できるか(もっともらしいか) 」を確率として計算します。確率同士は比較可能なので、計算結果を使ってランキングを作ったり、前提条件が異なっている結果同士を比較したり(よいモデルを探すときによく行われます) 、ということが自然にできるのです。
また、「 確率を通じて他の手法を組み合わせることができる」「 モデルによってはデータを生成できるという特徴を持つ(生成モデル) 」など、確率を使っているからこそのメリットが数多くあげられます。
こうしたメリットを求めて、もともと確率を用いない手法でも、確率的な手法に拡張されることが多いです。つまり、より効果的な手法を求めるなら、確率を用いた方法に行き着くということですね。
確率変数と確率分布
「確率」について、記号と用語の説明から始めましょう。
確率は p(X) という記号で表します。ここで X は「確率変数」 、 p(X) は「 X の確率分布」あるいは単に「 X の確率」と言います。X の取り得る値 a に対してその確率を p(X=a)、または簡単に p(a) と書きます。
この記法では、「 確率分布の種類は確率変数によって表される」ということに注意する必要があります。別の確率変数 Y の確率分布は、同じ p を使って p(Y) と書きます。2つの関数を表すときの f(x) と g(x) のような記法とは異なります。
p(X) が確率分布であるための重要な条件が2つあります。
確率の値は0以上1以下
すべての取り得る値の確率の合計は1
厳密には、事象や集合演算なども説明したほうがよいのですが、ここでは省略します。
おなじみのサイコロの例に当てはめて確認してみましょう。X はサイコロをふって出る目の「確率変数」 、p(X) がその「確率分布」とします。このとき、X の取り得る値は1から6までの6通りです。すべての目が同じ割合で出るとすると、「 確率の合計は1」という条件から、p(X=1) = ... = p(X=6) = 1/6 となります。
ところで、「 すべての目が同じ割合で出るとすると」とさらっと言いましたが、本当にそうでしょうか? 確率を初めて勉強したとき、「 1の目が出る確率は 1/6 って言うけど、サイコロを振っても1の目がちょうど6回に1回出るとは限らないよなあ」と思ったことはありませんか?
そのもっともな疑問に対し、「 無限回繰り返して平均すると、6回に1回出るんだよ」と説明され、一応納得しつつも「いやいや、サイコロを無限回とか振れないから!」と心の中で言い返したことはありませんか?
実は統計的機械学習の最終目的は、まさにそういった「有限回しか試行できない中で、すべての目が同じ確率で出ると言ってもよいか」という問題を工学的に(つまり現実的に)解くことなのです。
高校で確率をやったときにそのあたりの疑問で悩んだことのある人は、機械学習をとても楽しめると思います。
同時確率と条件付き確率
ここまで確率変数は1個でしたが、確率変数は複数個になる場合もあります。特に機械学習では、よほど簡単な例題でも複数の確率変数を持っていますので、複数個の確率変数を扱えるようになっておくことは必須です。
まずは先ほどと同じように、用語をさらっておきます。確率変数の個数は2個で説明しますが、3個以上でも同様です。
2個の確率変数 X, Y に対する確率分布を p(X, Y) と書き、XとYの「同時分布」または「同時確率」と言います。
確率変数 Y に何かある値が与えられているときのXの確率を p(X|Y) と書き、Yが与えられているときのXの「条件付き確率」と言います。
確率変数 Y は気にせずに、確率変数 X のみの確率を考える場合もあります。これは p(X, Y) の X に関する「周辺確率」と言い、単純に p(X) と書きます。
具体例を見ながら、この3つの分布がどういうものか説明します。せっかくなので、機械学習(自然言語処理)で実際に用いられる bag-of-words というモデルのミニミニ版を使いましょう。
bag-of-words では単語の並び方などは考慮せず、文章に単語が含まれているかどうかのみを考えて数値化します(含まれる=1、含まれない=0) 。使用回数をカウントするモデル(term-frequency)もありますが、今回は「含まれるか、含まれないか」のみを考えています。
このモデルで表現できる範囲は明らかに限られます。しかし、実現したいことが達成可能ならば、必要以上に複雑なモデルを考えないのは機械学習の鉄則です。このあたりのことは、前回のモデルの話 も参照してください。
それでは、モデルの構築は確率変数の設定から始めます。
Xは「文章に“ プログラム” という単語が含まれる」 、Yは「文章に“ アプリケーション” という単語が含まれる」を表す確率変数とします。それぞれ、含まれる場合が 1、含まれない場合が 0 という値を取ります。
本物の数字の方が説得力あるでしょうから、gihyo.jpのデベロッパステージの1560記事から各単語の出現確率を調べてみました。
p(X=1, Y=1) = 0.082
p(X=1, Y=0) = 0.271
p(X=0, Y=1) = 0.172
p(X=0, Y=0) = 0.475
上から「両方の単語が含まれる確率」「 “ プログラム” のみ含まれる確率」 、「 “ アプリケーション” のみ含まれる確率」「 両方とも含まれない確率」となります。
扱っている範囲はとても狭いですが、これも立派な「モデル」です。
ここで確率変数 Y はおいておき、確率変数 X のみの確率を考えてみましょう。
p(X=1)、つまり「文章に“ プログラム” という単語が含まれる」確率を求めるには、“ アプリケーション” も含む場合と含まない場合の両方を考えればいいので、次の式で求まります。
p(X=1) = p(X=1, Y=1) + p(X=1, Y=0) = 0.082 + 0.271 = 0.353
同様に p(X=0)、つまり「文章に“ プログラム” という単語が含まれない」確率も、“ アプリケーション” を含む場合と含まない場合を加えて、次のように計算できます。
p(X=0) = p(X=0, Y=1) + p(X=0, Y=0) = 0.172 + 0.475 = 0.647
p(X=0) と p(X=1) を足したら1になるはずなので、次の方法で求めることもできます。
p(X=0) = 1 - p(X=1) = 1 - 0.353 = 0.647
こうして求めた p(X=1) と p(X=0) が確率変数Xの「周辺確率」です。確率変数 Y の周辺確率も同様に求めることができます。演習問題にしますので、ぜひ確認してみてください。
次は、X=1 とわかっている場合の Y の確率を求めてみましょう。つまり「“ プログラム” という単語が含まれている文章に、“ アプリケーション” が含まれる確率」です。同時確率から、X=1 を満たしている確率のみ抜き出します。
p(X=1, Y=1) = 0.082
p(X=1, Y=0) = 0.271
上は「“ プログラム” が含まれ、かつ“ アプリケーション” も含まれる確率」 、下は「“ プログラム” が含まれるが、“ アプリケーション” は含まれない確率」です。これで良さそうですが、2つの合計は 0.353 となり、「 すべての取り得る値の確率の合計は1」という大切な条件を満たしていません。
この 0.353 という値は、先ほど求めた周辺確率 p(X=1) = 0.353 と一致しています。X=1 であることはすでにわかっているわけですから、p(X=1) = 0.353 の中での割合を新しい確率とみなす、つまり両方とも 0.353 で割れば、足して1になる確率が得られます。これが「条件付き確率」 p(Y|X) です。
p(Y=1|X=1) = p(X=1, Y=1) / p(X=1) = 0.082 / 0.353 = 0.232
p(Y=0|X=1) = p(X=1, Y=0) / p(X=1) = 0.271 / 0.353 = 0.768
同じように、 X=0 の場合の条件付き確率も求めておきましょう。
p(Y=1|X=0) = p(X=0, Y=1) / p(X=0) = 0.172 / 0.647 = 0.266
p(Y=0|X=0) = p(X=0, Y=0) / p(X=0) = 0.475 / 0.647 = 0.734
条件付き確率を用いると、「 “ プログラム” を使っている文章より使っていない文章のほうが、“ アプリケーション” が使われる可能性が高い」といった情報を確率で表現することができます。
p(X|Y) も同様に求めることができます。こちらも演習問題としておきますので、試してみてください。
確率の加法定理・乗法定理
これらの計算方法を公式の形でまとめたのが「確率の加法定理・乗法定理」です。
確率の加法定理
2個の確率変数 X, Y について、その同時確率 p(X,Y) と周辺確率 p(X) の間に次の等式が成り立つ。
右辺のΣは、確率変数Yのとりうる値すべてにわたって足しあわせる。
確率の乗法定理
2個の確率変数 X, Y について、その同時確率 p(X,Y)、条件付き確率 p(Y|X)、周辺確率 p(X) の間に次の等式が成り立つ。
p(X, Y) = p(Y|X) p(X)
乗法定理は、条件付き確率と周辺確率から同時確率を求めるだけでなく、そのうち2つから残る1つの確率を求めることができることに注意してください。実際 p(Y|X) の計算では、周辺確率と同時確率を使って条件付き確率を求めていました。
加法定理のことは「確率分布を周辺化する」とか「p(X,Y) からYを積分消去する」とかいった言い方をすることも多いです。
また、条件付き確率と同時確率は見た目が似ていますが、同時確率から条件付き確率を求めることができるのに対し、条件付き確率だけから同時確率を求めることはできません。つまり、条件付き確率は同時確率より情報量が少なくなっています。
このことは、機械学習のいろいろな演算を直感的に理解するのに効いてくるので、憶えておくと役に立ちます。
実は統計的機械学習は、この2つの定理を繰り返し繰り返し用いて最終的に求めたい確率を導くのが基本手順になります。確率の加法定理と乗法定理を掛け算の九九と同じくらい空気のように使いこなせるようになれば、機械学習はマスターしたも同然!! ……っていうのはさすがにちょっとだけ言い過ぎですね。すいません。
事後確率とベイズの公式
同時確率 p(X,Y) に対する条件付き確率は、Y の値を与えた場合の p(X|Y) と、X の値を与えた場合の p(Y|X) の2通りが考えられます。X と Y が全く同時に起きる場合(例えば2個のサイコロを振ったそれぞれの目など) 、この2つの条件付き確率はどちらも無理なく考えることができます。
一方で、X が先に起きるべきである、あるいは X がモデルのパラメータで Y は観測値、などの「 X の値を決め、その後初めて Y の値を決めることができる」モデルでは、Y の値を与えたときには X の値はすでに決まってなければならないため、p(X|Y) は何の「確率」かわかりません。
確率を「どれくらい起こりうるかを表す値」と定義するうちは、そのような値は存在しないことになってしまいます。ひとまず後先のことはおいといて、このような条件付き確率 p(X|Y) を「事後確率」または「事後分布」と呼び、形式的に話を進めることにしましょう。
事後確率 p(X|Y) は、形の上ではただの条件付き確率の一つです。そこで乗法定理を Y についてと、X についての2通り使うことで、次の等式が成り立ちます。
p(X, Y) = p(X|Y) p(Y) = p(Y|X) p(X)
2項目と3項目を p(Y) で割ると、「 ベイズの公式」と呼ばれる次の等式が導かれます。
これは機械学習の教科書で非常によく用いられる公式ですが、確率変数が2個のわかりやすい問題ならともかく、もっと複雑なモデルで使う場合は間違いやすいです。
ここで導いたように、同時確率を2通りに展開して毎回考える方が間違いにくく、ブラックボックスにならず、「 ベイズの公式ってどういう順番だったっけ?」とならずに済むので、おすすめです。
しかし、「 事後確率」なんて気持ち悪いものを認めてしまって本当に大丈夫かと、心配になりますか?
ここで少し歴史の話でもしてみましょう。「 事後確率」について最初に言及したのは18世紀の数学者、トーマス・ベイズです。
高校数学での確率のような「どのくらい起こりうるか」という考え方では都合が悪いことに気づいたベイズは、確率を「どれくらい信用できるか(もっともらしいか) 」を表す量(信念の度合い)として広く再定義します。すると、さきほどの p(Y|X) も「与えられた Y は、どの X から導かれたと信じられるか」を表す値となり、事後確率が意味のある存在になったのです。
数学者としてベイズを紹介しましたが、ベイズの本職は実は牧師でした。いわゆる「市井の数学者」 、アマチュアだったのです。一方のラプラスは、当事すでに数学者として大きな実績を持っていました。彼の名前で発表したら、もっと大きな問題になると考えたのでしょう(なにしろ、今でも一部では論争が続いているそうですから……) 。
その論争に参加するのも別の意味で楽しそうですが、ここではやはり「どれくらい信用できるか(もっともらしいか) 」を新しい確率の定義と認めることにしましょう。新しい定義によって様々な不確かさを足したり掛けたり比較したりできる「確率」で表せるようになり、機械学習の力は大きく広がるのですから。
機械学習に限らず、様々な統計的手法の発展に大きく貢献したその新しい確率は、ベイズの名を冠して「ベイズ的確率」と呼ばれています。現在では、様々な分野でベイズの名前がついた技術が用いられています。アマチュア数学者だったベイズ自身は、何百年も後に、自分の名前がこれほど多くの分野の多くの人の口にのぼるとは、まさか夢にも思わなかったでしょうね。
モデルのパラメータ数
確率における、もう一つの重要な概念である「独立性」の話をしたいのですが、その前に一度「文章に含まれる単語」のモデルに戻ります。
X は「文章に“ プログラム” という単語が含まれるか」 、Y は「文章に“ アプリケーション” という単語が含まれるか」を表す確率変数で、それぞれの確率は以下のようになっていました。
p(X=1, Y=1) = 0.082
p(X=1, Y=0) = 0.271
p(X=0, Y=1) = 0.172
p(X=0, Y=0) = 0.475
この同時確率全体は4個の値を持っており、またこれらの値がわかっていれば、このモデルは完全に記述できます。また、確率は総和が1であることから、実質は3個の値がわかれば残りの1つは自動的に決まるため、このモデルのパラメータ数は3であると言えます。
それでは、モデルで扱う単語がもう1つ(例えば“ インターネット” )増えて3種類になった場合、そのモデルを完全に記述するのに必要なパラメータ数は何個になるでしょう。
3番目の確率変数を Z とすると、X, Y, Z のそれぞれが1か0かの2通りの値を取り、それぞれごとに同時確率の値を定める必要がありますから、全体で 23 = 8 個。総和が1の条件から1個減らせて、パラメータ数は7個とわかります。
さらに単語を100種類に増やした時は、同様の考察から、パラメータの個数は 2100 - 1 ≒ 1030 個であることがわかります。
ずいぶんパラメータが増えてしまったようですが、どれくらいのメモリがあればこのモデルを実装することができるでしょう?
1個の値に4バイト使う単純計算だと、4,000,000,000,000,000,000テラバイトほどあれば足ります。これは無理です。そしてこれでもまだ、100種類の単語しか考慮できていないのです。
一般に人間の語彙は2万~10万と言われていますが、とてもそんな単語数を扱うことはできそうにありません。どうすればこのモデルを現実的なものにできるでしょう。
確率変数の独立性と「よいモデル」
ここで天下りですが、「 確率変数の独立性」を定義します。
確率変数 X と Y について p(Y|X) = p(Y) が成り立つとき、X と Y は「独立」であると言います。ちなみにこのとき、X と Y を逆にした p(X|Y) = p(X) も成り立つことが乗法公式から言えます。
p(Y|X) = p(Y) とはつまり、Y の確率は X の値に寄らないということです。X=1 でも、X=0 でも、はたまた X の値が不明でも、Y の確率に変化はないということです。関係性がないことを「独立」と言うわけですね。
先ほどの単語2種類のモデルでは、
p(Y=1|X=1) = 0.232
p(Y=1|X=0) = 0.266
p(Y=1) = 0.254
でしたから、X と Y は独立ではありません。
独立性の条件を言葉で言い替えると、「 文章に“ プログラム” という単語が含まれていてもいなくても、“ アプリケーション” という単語が含まれる確率は変わらないか?」ということになります。
相関性の高い言葉は同じ文章の中で使われる確率が高いだろうし、逆なら低いだろうから、このモデルが独立でないことは直感的にも自然でしょう。
確率変数 X と Y が独立ではないことを十分わかってもらえたところで、そこをあえて「X と Y は独立である」と仮定します。明らかに矛盾した話ですが、しばらくお付きあいください。
この仮定のもとでは、次の式が成り立ちますから、p(X) と p(Y) がわかれば同時確率が求められます。
p(X, Y) = p(X|Y)p(Y) = p(X)p(Y)
具体的には、p(X=1) = 0.353, p(Y=1) = 0.254 の2つの値から p(X=0) = 1 - 0.353 = 0.647, p(Y=0) = 1 - 0.254 = 0.746 が求まり、すべての同時確率が計算できます。
p(X=1, Y=1) = p(X=1) * p(Y=1) = 0.090
p(X=1, Y=0) = p(X=1) * p(Y=0) = 0.263
p(X=0, Y=1) = p(X=0) * p(Y=1) = 0.164
p(X=0, Y=0) = p(X=0) * p(Y=0) = 0.483
モデルを表すのに必要なパラメータは p(X=1) と p(Y=1) の2個になり、1つ減らすことができています。
単語3種類のモデルでも、3個の確率変数 X と Y と Z のどの2つの間も独立である(これを単純に「 X と Y と Z が独立」と言います)と仮定すると、p(X=1) と p(Y=1) と p(Z=1) の3個のパラメータからすべての同時分布を求めることができます。
さらに単語が100種類に増えても、同様にパラメータの数は100個で足ります。もともと 2100 - 1 ≒ 1030 個だったのがウソのようです。これなら単語がもし100万種類に増えたとしても、パラメータ数も100万になるだけであり、コンピュータで扱う分にはほぼ問題ありません。
しかし、パラメータ数が多すぎる問題は解決しそうですが、こうして求めた同時確率は、「 同時確率の本当の値」と異なってしまっています。これは、独立でないものを独立と仮定してしまったせいです。
今回の例ではその誤差は小さいですが、単語によってはもっと大きな違いが生まれることもあるでしょう。すると、このような不正確な手法には意味がない、と判断するべきでしょうか?
しかしどんなに正確であったとしても、計算できないモデルにはもっと意味がありません。機械学習では、「 計算できること」が最大の正義であり、計算コストと結果の価値のバランスが大切になります。計算が簡単かつ十分よい結果がでるのが「よいモデル」なのです。
そのためであれば、正確さが多少(場合によっては多々)損なわれる仮定であっても、あえて採用します。
独立性を持つモデルは(仮定だったとしても、本来持つ独立性だとしても)そうでないモデルより計算がかなり簡単になります。また独立性以外にも計算コストを下げる様々なテクニック(近似法)が数多くあります。そうして出てきた結果が「よい結果」かどうかを評価する必要もあります。それら近似法や評価方法などについては、その機会ごとに説明します。
ナイーブベイズによる文書分類
最後に、ここまでで解説した事後確率と独立性の仮定を使って得られる、文章をカテゴリごとに分類するためのモデルを紹介しましょう。
X を「文章のカテゴリ」 、Y1 , Y2 , …… を「文章に単語が含まれるかどうか」を表す確率変数とします。Y の添え字ごとに対応する単語はあらかじめ決まっているものとします。
gihyo.jpには「デベロッパステージ」「 アドニミストレータステージ」「 WEB+デザインステージ」というコーナーがありますので、これを文書のカテゴリとして考えましょう。
簡単のため「デベロッパステージ」と「アドニミストレータステージ」の2つのカテゴリに制限し、各ステージの記事の割合を X の確率とすれば良さそうです。実際の値は、次のようになっていました。
p(X=dev) = 0.652
p(X=admin) = 0.348
ただし、確率変数 X=dev は「デベロッパステージ」を、X=admin は「アドミニストレータステージ」を指すものとします。
ここで条件付き確率を使うと、「 デベロッパステージでは“ プログラム” という言葉をよく使いそうだけど、アドニミストレータステージではあまり使わなさそう」といった情報を数値化することができます。
そこで、文章に“ プログラム” が含まれる確率(=Y1 )を各ステージごとに調べてみました。
p(Y1 =1|X=dev) = 0.271
p(Y1 =1|X=admin) = 0.136
条件付き確率 p(Y1 =1|X=dev) は「デベロッパステージの文章で、“ プログラム” が含まれる確率」です。X=admin の方も同様です。
確かに p(Y1 =1|X=dev) > p(Y1 =1|X=admin) となっていますね。
同じように、確率変数 Y2 を「文章に“ アプリケーション” が含まれる」として、その確率を求めておきましょう。
p(Y2 =1|X=dev) = 0.172
p(Y2 =1|X=admin) = 0.523
それでは「“ アプリケーション” は含まれているが“ プログラム” は含まれていない文書」があったときに、それがどのカテゴリの文書かを判断したいとします。
この条件に対応する確率変数は Y1 =0, Y2 =1 ですが、カテゴリを表す X の値はまだわかっていません。ここで、p(X=dev|Y1 =0, Y2 =1) と p(X=admin|Y1 =0, Y2 =1) を求めれば、その確率の大きい方が「信用できる X の値」をさしている、と判断することができます。
文章を書くときに、中身を書いてからカテゴリを考える、なんてことは普通ありませんよね。つまり、p(X|Y1 , Y2 ) はまさに事後確率であり、これを計算することは、実際にそこにあるもの(観測値)から隠れた情報(例えば「この文章はデベロッパーステージに載せるつもりで書いたよ!」 )を推測する手段であるわけです。
この一連の流れが、統計的機械学習の代表的な考え方の一つになっています。
ベイズの公式を使うと事後確率を求める式を得られますが、乗法定理を使って同時分布を2通りに展開した方が、魔法を使ったわけではないことが目に見えてわかりやすいでしょう。
p(X, Y1 , Y2 )
= p(X|Y1 , Y2 ) p(Y1 , Y2 )
= p(Y1 , Y2 |X) p(X)
第2式と第3式から、p(X|Y1 , Y2 ) は次の式で求めることができます。
式の右辺を計算できるか考えてみましょう。
分子にある p(Y1 , Y2 |X) について、Xが与えられているときに Y1 , Y2 が独立である(これを「条件付き独立」と言います)と仮定すると、先ほどの同様の議論から p(Y1 , Y2 |X) = p(Y1 |X) p(Y2 |X) が成り立ちます。
p(X) と p(Y1 |X) たちはわかっていましたから、これで右辺の分子は求めることができました。
次に分母の p(Y1 , Y2 ) ですが、これは分子を「Xについて周辺化」することで求められます。
具体的には、乗法定理から p(Y1 , Y2 |X) p(X) = p(X, Y1 , Y2 ) が言え、ここから加法定理を使ってXを消すと p(Y1 , Y2 ) になります。最初のほうで「機械学習では加法定理と乗法定理を繰り返し繰り返し使う」「 加法定理は周辺化とも言う」と言及していたことを思い出してくれました?
ただし、この分母の p(Y1 , Y2 ) には X が入っていない( X によらない)ので、「 p(X|Y1 , Y2 ) が一番大きい X を求めたい」だけであれば、実は分子だけを比較するので事足ります。
それでは最後に、「 “ アプリケーション” は含まれているが“ プログラム” は含まれていない文書」 、つまり Y1 =0, Y2 =1 が与えられたときの事後確率を計算してみましょう。
まず X のそれぞれの値について、分子を求めます。
p(Y1 =0, Y2 =1|X=dev) p(X=dev)
= (1 - 0.271) * 0.172 * 0.652
= 0.082
p(Y1 =0, Y2 =1|X=admin) p(X=admin)
= (1 - 0.136) * 0.523 * 0.348
= 0.157
分母はこれを周辺化したもの、つまり2つの値を足すと得られます。
p(Y1 =0, Y2 =1)
= p(X=dev, Y1 =0, Y2 =1) + p(X=admin, Y1 =0, Y2 =1)
= 0.082 + 0.157
= 0.239
そして、事後確率は次のようになりました。
p(X=dev|Y1 =0, Y2 =1)
= p(Y1 =0, Y2 =1|X=dev) p(X=dev) / p(Y1 =0, Y2 =1)
= 0.082 / 0.239
= 0.343
p(X=admin|Y1 =0, Y2 =1)
= p(Y1 =0, Y2 =1|X=admin) p(X=admin) / p(Y1 =0, Y2 =1)
= 0.157 / 0.239
= 0.657
どちらかより適したカテゴリと判断できるか、もうおわかりですね。
ここで用いた「条件付き確率のもとでの独立性」は「条件付き独立」あるいは「ナイーブベイズ」「 単純ベイズ」と呼びます。ナイーブベイズを仮定した今回のモデルは「ナイーブベイズモデル」 、それを用いたスパム判定が「ベイジアンフィルタ」です(ベイズさんの名前を連呼しすぎですね) 。
もちろん、ここでの「条件付き独立」はあくまでも仮定であり、本当は独立ではありません。しかしこの大胆な「近似」にもかかわらず、ナイーブベイズは十分精度の高い判断が行えることが知られています。簡単な計算でよい結果の出る「いいモデル」ということになります。
実際、ナイーブベイズは文書分類やスパムフィルタにとてもよく使われる手法です。ナイーブベイズは、カテゴリや単語の種類が2個ではなくもっと一般の場合についても同様の方法で考えることができます。
次回の実践編では、ナイーブベイズを題材に、確率の計算をどのように実装するかを紹介します。