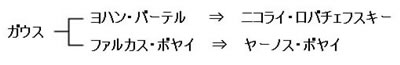世界を変えた二人の若い数学者
歴史に秘められたエピソードとか意外性に富む話は、まさに事実は小説より奇なりというように、おもしろいものである。
ユークリッド幾何を超えて、双曲幾何が生まれる歴史の一断面をとってみただけでも、ドラマ性に満ちた紆余曲折がある。
『ピタゴラスの定理でわかる相対性理論』 エジプトに源を発した幾何学からアインシュタインの双対性理論までの物語を、意外性を含めて語ったものである。
その中で双曲幾何は、天才数学者ガウスと親交のあった2人の数学者の"弟子"が、ロシアとハンガリーで開拓したものであることを書いた。このあたりのことを少し補足しておきたい。
まず、この系譜は次のようである。
まず、ガウスよりは数歳上でいわば最初の数学教師でありながら彼の友人でもあったバーテル(Johan Bartels 1769-1833)がいた。バーテルはスイスで教えていたが、ロシアのカザンに大学ができたときに教授として招聘された。そこに最初の学生の一人として、ロバチェフスキー(Nikolai I. Lobachevski 1793-1856)が入学してきた。
ガウスのもう一人の親友が、ゲッチンゲン大学時代のクラスメートでハンガリーから留学していたファルカス・ボヤイ(Farkas Bolyai 1775-1856)だった。
図1 の絵葉書は、1799年にゲッチンゲンの天文学教授Seyferが、ファルカス・ボヤイに送ったもので、当時のゲッチンゲンの風景であると思われる。
天文学教授Seyferがファルカス・ボヤイに送った絵葉書
Seyfer教授は、彼の家でボヤイとガウスを引き会わせた。ファルカス・ボヤイが国に帰ってから育てた弟子とは一人息子のヤーノス・ボヤイ(János Bolyai 1802-1860)である。
話がちょっとそれるが、数学の天才が現われたとき、その国やその文化圏では秀でた芸術家も出現していることも面白い。どうも数学や物理学はそれだけではなく、音楽や美術など様々な文化と綾なしながら、物語が展開されているようだ。
先の本にも書いたが、ピタゴラスが研究した純正律を超えた平均律音階が本格的になったのは、巨匠バッハの平均率ピアノ曲集からだった。ちなみにモーツアルトは、ガウスが正17角形の作図に成功する数年前の1791年に35歳の生涯を閉じている。
文武両道で一芸に秀でいる、ヤーノス・ボヤイ
ヤーノス・ボヤイが、父の著作『若き学徒のための数学入門:試論』への付録として、『 空間の科学』という新しい幾何を書いたのは1831年、つまり29歳のときである。そのとき、モーツアルトの再来と言われたピアニストで作曲家のリスト(Franz Listz 1811-1886)は20歳、祖国(ハンガリー)は20歳、祖国(ハンガリー)を離れてパリにいた。彼はバイオリンの鬼神と呼ばれたニコロ・バガニーニの演奏を聴いて感銘を受けて、自らはピアノの超絶技巧を目指した。
当時のハンガリーは、政治的にオーストリアの強い影響力のもとにあった。リストの母親もオーストリア人でありドイツ語を使って彼を育てた。ヤーノスはウイーンで工学を学び、軍人としての訓練も受け、剣ではオーストリア・ハンガリー帝国軍No.1の達人であり、それにバイオリンを弾かせても一流だったという。リストとヤーノスの共演というフィクションがあっても決しておかしくないと思う。
ガウスとボヤイ親子
ヤーノスの『空間の科学』は、ゲッチンゲンの天文台長で教授になったばかりのガウスに、父ファルカスから1831年6月20日の日付で届けられた。賞賛を期待していた父ファルカスへの返信は、「 すでに自分でも長年研究したことであり、ご子息がこれ以上この問題にかかわるのは感心しません」というふうなものだった。
一方のロバチェフスキーの仕事に対して、ガウスはある程度の理解を示したようだ。ロバチェフスキーは、やがて母校カザン大学の学長として出世した。
ヤーノスの父ファルカスは、学生時代から平行線の永久問題を解くことに情熱を燃やして、ガウスと議論をしてはその論理の瑕疵を指摘されていた。ヤーノスは、父が果たせなかった夢を達成したと思ったが、自分より先にガウスが第5公準を否定して新しい幾何をつくる発想を得て研究を進めていたことを知って、数学への意欲を失なってしまった。
1832年にガウスがゲーリング(Christian Gerling 1788-1864)にあてた手紙には、ヤーノスが第一級の天才だと言いながら、実際には父子に対して冷淡であり、ロバチェフスキーの存在すら知らせていなかったのが不可解である。このあたりの裏の事情を詮索しようとしてはいけないだろうか?
ファルカス・ボヤイは、息子の自慢話をガウスへあてた手紙に書いている。それに対してガウスは、自分の息子は身体がひ弱で、数学の才能には恵まれていないことを認( したた ) めている。ガウスにしてみれば、親友とは言えファルカス・ボヤイの自慢話は、うっとうしくはなかっただろうか?
当時、親しい間柄の青年同士は、手紙にずけずけとものを言う習慣があったのかもしれない。例えば、父ファルカスがガウスにあてた手紙で、お前の娘が自慢息子と危険な関係になるような可能性はないだろうなとか、お前のワイフはお風見鶏のように気分をくるくると変えるような女性ではないだろうな、などと言っている。親友とは言え、偉くなっていたガウスには、ムッとくる手紙ではなかっただろうか?
一方、ファルカスは地方の名門の出で名士でもあったから、ガウスから冷淡に扱われた息子のヤーノスが精神的に苦しむようになったことに、耐えられなかったに違いない。
才能を育てるにはトレーナーが重要
科学の歴史もそうだが、野球やサッカーのようなスポーツの名プレーヤを輩出するメカニズムには、監督だけでなく、トレーナーが重要である。科学史に登場する天才は、いろいろなやり方で、教師(トレーナー)を超えた。
アインシュタインは、幾何学の専門家ミンコフスキーの授業をサボって超えた。
ヤーノスは、父がこだわっていた永久問題を解く(第5公準を他の4つの公準から証明する問題)のではなく、第5公準を捨てた幾何を目指すことによって、父を超えた。
ロバチェフスキーもバーテルを、そのようにして教師を超えた。
ヤーノスの場合は、超えたことをガウスによって否定されたと思ったに違いない。ユークリッド幾何を超えるために人生を営んできたのに、それが認められなかったのだ。
そのためかヤーノスは、肖像画を自分の剣でずたずたに切り裂いてしまったといわれている。ファルカスの肖像画は残っているが、ヤーノスのものは現存しない。彼の業績に光が当てられたのは、没後の1867年である。
その年に、たまたま(ヨーロッパに起きた政治的混乱のあと)オーストリアとハンガリーが対等の関係の二重帝国が成立している。ハンガリーの人々が、ヤーノスへの熱狂的な崇拝の念を持つようになったのは、タイミングの助けもあったように思える。
ハンガリーは、第一次世界大戦によって、二重帝国が崩壊し政治的な不安定に陥ったときに、隣国ルーマニア軍による侵攻を受けた。
そして、ボヤイ親子がうまれ育ったトランシルバニア(Transylvania)地方は1920年のトリアノン条約によってルーマニア領になってしまったことも、ハンガリーの人々に数学史に画期的な革新をもたらした父子への想いを一層熱くしたのではあるまいか。
写真 は、マロスバーシャールヘイ(Marosvásárhely、ボヤイ父子が住んでいた町;ルーマニア名Tirgu-Mureş、ティルグ・ムレシ)にあるボヤイ博物館に展示されている擬球である。また「ピタゴラスの定理でわかる相対性理論」のp.183の肖像もこの博物館に展示されている。
ボヤイ博物館に展示されている擬球
ここに、ボヤイ父子に関する資料の収集家であるDr.Péter G.Szabóの名を挙げておきたい。同氏は、セゲド(Szeged)大学の情報工学科(Institute of Informatics, Department of Applied Informatics)の準教授で、情報理論のほかに数学歴史の研究家でもある。日本での研究歴もあって、日本の各地の神社に奉納されている算額資料の収集にも熱心である。
今回の絵葉書も同氏から入手したものである。
Dr.Péter G.Szabóホームページ: http://www.inf.u-szeged.hu/~pszabo/