ヴァチカン図書館の写本

本書のp15で説明しているユークリッドが著した，『⁠幾何学原本』は羊皮紙に書かれたものですが，現存はしていません。

けれども，ユークリッドの原本は東西文化の交流をとおして伝えられ，アラビア語，ギリシャ語，ラテン語の写本が伝承されています。

ヴァチカンの図書館には多くの写本が保存され，図面を一枚いくらで分けて貰うことも出来ます。こうした貴重な資料を研究しようとする試みもあります。

ここでの写本をインターネット上で勝手に公開するのは，色々と問題があります。そこで，原本のゲラルドによるラテン語写本の一つでRossianus579と呼ばれているものから，三平方の定理の証明の図をまねて，私が描いてみました（図. ピタゴラスの定理⁠）⁠。

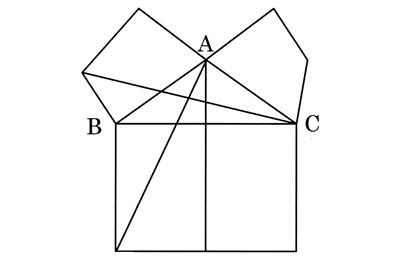
本書ではp20にありますが，直角三角形ABCのそれぞれの辺に，正方形が三個描かれている有名な図です。

Rossianus579の図では，直角も不正確ですが，二等辺三角形になっています。また，それぞれの辺に四角形もいびつでとても正方形にはほど遠いものです。けれども証明に必要な補助線はしっかりと入っています。

このように，写本の図では，一般に成り立つ定理に対して，特殊な場合の図が描かれていることが幾つもあります。

例えば，一般の三角形で成り立つ内容を，二等辺三角形や直角三角形を使って証明しているのです。

また，定規のような文具も発達していなかったのか，交点がうまく交差していない図もあります。

ギリシャ語の写本Vat.Gr.190は，図もきれいで正確なため，これをもとに各国語に翻訳されて出版されています。

こうして民族の移動や戦いなど多くの歴史的なドラマを経て，３千年以上昔の英知がこのように伝えられていることに雄大なロマンを感じます。