レーデルとアインシュタインとの出会い

今月は，相対性理論の幾何学に重要な足跡を残したエンリク・レーデル（Enrique Loedel Pulumbo, 1901-1962）に光をあててみたいと思います。

レーデルが南米ウルガイの首都モンテビデオに生まれたのは，20世紀が明けて間もない1901年です。

彼が隣国のアルゼンチンの大学に留学して，相対性理論の研究をまとめるとき，幸運にもアインシュタインに会って，ディスカッションする機会に恵まれたのです。

それは，ベルリン大学教授だったアインシュタインが，1925年に南米を訪問したときです。正確には4月16日の午後，アインシュタインがブエノスアイレスの科学アカデミー（Academia Nacional de Ciencias Exactas, Físicasy Naturales）で栄誉を受ける儀式が行われ，出席者とのあいだで質疑応答をしました。

そこにレーデルもいて，質問してアインシュタインと一般相対性理論についてディスカッションしました。その年，彼はPh.Dを取得し若くして教授になっています。そして翌年の1926年には，そのときのディスカッションに関係するテーマで，ドイツの物理学論文誌に寄稿しています。

ところでアインシュタインは，レーデルの質問のことをどのように評価していたのでしょうか。彼の日記には，あまり良くは書かれていなかったようです。

物理学研究の中心地で過ごす

さて1926年といえば，ヨーロッパの物理学としては画期的な年でした。チューリッヒ大学にいたシュレディンガーが，波動力学の論文を4編書き，量子力学の発展に旋風を巻き起こします。

そして1927年に，マックス・プランクの要請をうけて，彼はベルリン大学に移りました。このような時にレーデルは，ドイツに留学してシュレディンガーやプランクのもとで研究しますが，教育に専念するために1930年にアルゼンチンにもどりました。

その後ドイツでは，ヒトラーの台頭によって，ベルリン大学もユダヤ人排斥の嵐に巻き込まれ，アインシュタインやシュレディンガーもドイツを離れることになります。

レーデルは，ベルリン大学の物理学研究が世界の中心のときに，20代後半をそこで過ごしたわけです。

ローレンツ変換とレーデル線図

本書『ピタゴラスの定理でわかる相対性理論』に，レーデル線図として紹介したローレンツ変換の幾何学的方法をレーデルが発表したのは，アインシュタインとの最初の出会いから23年後です。

ローレンツ変換

ローレンツ変換とは，本書で詳しく説明しているように，ある事象を2つの座標系S(t,x)とS' (t',x' )で見たときの時間と位置の相互関係を与える変換式のことです。

それを簡単な幾何の手法で計算するレーデル線図を，日本で最初に紹介したのは本書ですが，ここで改めてその意味を明らかにしておきたいと思います。

ミンコフスキーの幾何

1905年にアインシュタインが相対性理論を発表すると，彼の大学時代の数学の教師だったミンコフスキーが，相対性理論を幾何学的に展開をして発表したのは1908年です。

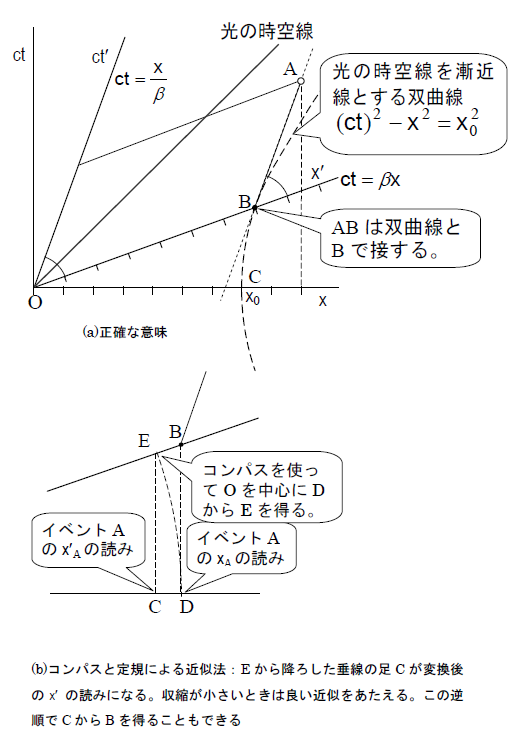
しかしミンコフスキーの幾何には，ある欠陥がありました。それは『ピタゴラスの定理でわかる相対性理論』のp.149で図7.12として紹介したのですが，x 座標の目盛りとx'の目盛り， ct の目盛りとct'との目盛りが異なります。目盛りの変換が複雑で定規とコンパスの簡単な操作では正確な変換をすることが大変です（図1参照）⁠。

簡単にローレンツ変換するレーデル線図

目盛りの変換なしに，定規とコンパスだけで簡単にローレンツ変換する方法が，レーデル線図です。これはピタゴラスの定理を使うもので，まさにコロンブスの玉子のような発想によるものでしたが，ミンコフスキー以来40年後だったというのが驚きです。

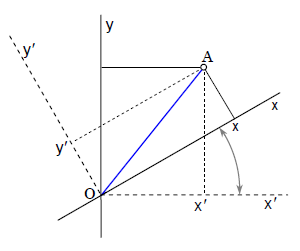
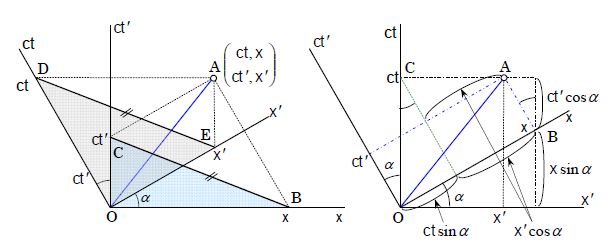
本書の第1章最後のページでも書いているように，パルテノン神殿の妖精が，図2のように笑って語っていることにヒントがあったのです。レーデル線図の説明を図3（左）に示しています。

なお，本書にはブリーム線図というものも紹介しています。これはRobert W. Brehme（米国Wake Forest University教授）が教職について3年後（1962年）⁠，レーデル線図のことに気づかずに，アメリカの物理学関係論文誌に発表した類似の方法で，図3（右）です。