今回は、
- 「6.
11 双曲ピタゴラスの定理を計算する」 (p. 122)
を公開することにします。

図1のような直角三角形の3辺の間には有名な関係として、
![]()
が成り立つことはほとんどの読者の知るところです。しかし双曲幾何では、
![]()
となることが本書の大きなテーマです。
図2は本書の図6.
ここでは、
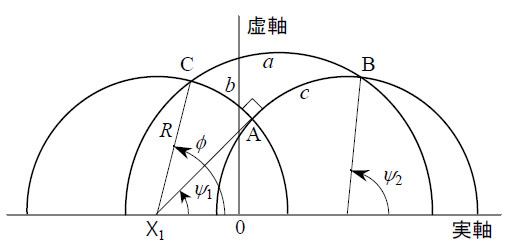
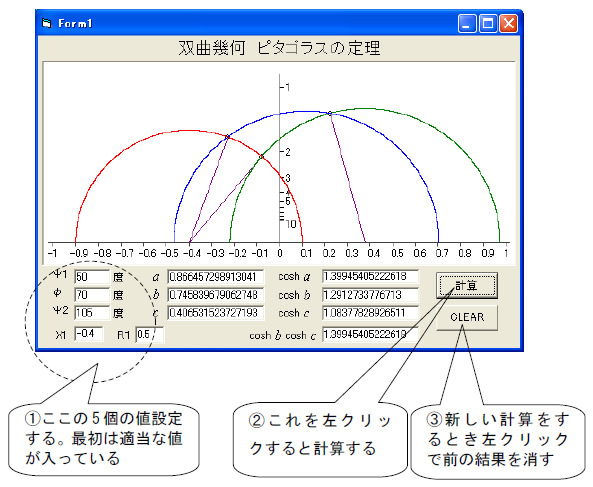
図3は、
2008-02-29
今回は、
を公開することにします。

図1のような直角三角形の3辺の間には有名な関係として、
![]()
が成り立つことはほとんどの読者の知るところです。しかし双曲幾何では、
![]()
となることが本書の大きなテーマです。
図2は本書の図6.
ここでは、

図3は、

おすすめ記事