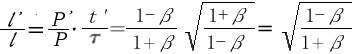前回 はアインシュタインの1905年9月のAnnalen論文の全訳と解説を提供しました。解説の中で次のように書きました。
マイケルソン-モーレイの実験から、アインシュタインが時間や距離に関して当たり前ではない結論を導いて6月論文を書き、その後も思考と計算に没頭してさまざまな理論的帰結を得ながら、当たり前ではない公理から驚くべき物理の法則を導いたのです。この論文はきわめて短く、序論のようなものはほとんどありません。単刀直入です。しかし難解なのが定数Cに関係する論理です。本来なら丁寧に書きたいあるいは書くべきものがあったと思うのですが、省いています。
こう書いたあとで、あれこれと考えたのですが、このときのアインシュタインの洞察は広範にわたってそれぞれで深いものだったのだな、と思うようになりました。その中の一つが9月論文の最初に出てくる
です。
光や電磁波のエネルギーは系(と系(では違った値として観測されるのですが、その関係を与えるのがこの式です。系(で観測されるエネルギーがl 速度v (ではl' この関係がどのような論理で得られるのか説明しようと思います。
これを前提の一つとしてE=mc2 私どもは(1)式が導かれるプロセスを理解したいと思うわけです。実はこの式の誘導は6月論文に克明に記述されているのですが、その部分を前回のように翻訳して説明しても決してわかりやすいプレゼンになりそうもありません。
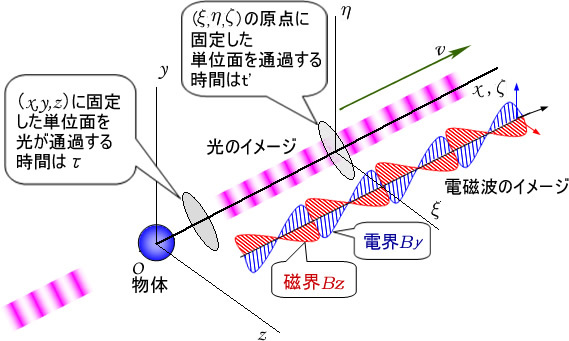
そこですこし違う論理にします。しかも図1 のような設定で次の関係を証明するというか導いてみましょう。
図1 t=0で物体が光や電磁波の放射を開始したとき両座標系の原点は一致しているまず、「 第6回 光とは何ぞや 」の表1に示されている式からスタートします。ここで再掲して説明を補足したいと思います。
表1 ( 再掲)時空と電磁界のローレンツ変換
変数 ローレンツ変換式 時空 x:位置 電磁現象 E:電界強度
相対性理論の一般的な読み物にしても入門書でもそうですが、この表の①と②のことはよく書いています。しかし③④について書いてある本はまれです。つまりほとんどの相対性理論の語り口は、ニュートン力学の時間の概念を作り変えて位置と時間と速度の関係を書き換えたという物語です。
その当時の物理学は、ニュートン力学とマックスウェルの電磁気学が2つの柱でした。アインシュタインの3月論文は、今でいう光量子の概念を提出しQuanta(量子)という用語がしきりに出てくるのですが、これが認められるまでに15年ほどかかっていますので、3番目の量子力学という発想はまだありませんでした。
ベッソーとの議論
この論文とブラウン運動に関する論文の後だと思われる1905年の早春、アインシュタインはニュートン力学と光の性質とのあいだの矛盾を解こうと全力を注いで考えていました。
ベッソーに議論の相手になってくれるように頼み、いろいろの側面から集中的な議論を続けました。時間に関するErnst Machの説も重要な思考素材でした。
当然のことながら、アインシュタインの研究家はこの当時のことに大きな関心をもって書いています。FoxとKeckのEinstein A to Z ベッソーとは17日間議論したということです。
Denis BrianのEinstein-a life 最後の晩のベッソーとの議論でも疑問が解消できず、既知の実験事実からは真の物理法則を見つけることは無理だろうと思って疲れ果ててアパートに戻ります。しかし翌朝、アインシュタインの頭のなかで嵐が吹き始めて答えが出てきて、最後のジグソーパズルが解けたとされています。そして、ベッソーには淡々と「( 昨日は)ありがとう。問題がすっかり解けたんだよ」と語ったのですが、どのような解であるかはそこでは話していなかったようです。というよりもそれは不可能だったと筆者は思います。
頭のなかで統合したのが一瞬であって、それを整然とした論文にするのには数カ月を要するのが普通です。しかし、彼は数週間で6月論文を書き上げました。
この論文の最初に、ファラディーの電磁誘導が磁界とコイルの相対運動によるものとして引用していることから推測すると、さらにエーテルの仮説を排除してマックスウェルの電磁方程式をよく考察すると、座標系によらずに電磁波の速度がcになることを確認して、時間の概念について書き換えられなくてはならないのはニュートン力学だ、という結論に達していたのだと考えられます。
この思考のプロセスを経て、時空と電磁現象が共通の性質をもっていることをアインシュタインは提唱したのです。それをまとめたのが表1です。③と④が電界と磁界の関係ですが、図1を見てください。ここには光の平面波のイメージとして赤の縞模様を使い、電磁波のイメージも脇に描いてみました。磁界と電界は、互いに直角のベクトルの関係にあって、同じ位相の正弦波で伝播します。伝播の方向は両者に直角の向きです。
表1の4個の式は、いずれも物体の質量には言及していません。しかし9月論文では、時空と電磁現象とを統合して論じて、質量m (1)式の関係です。図1のように(2)式になります。
(証明)
では(2)式を証明してみます。
まずこの表の③と④より次式が得られます。
ここで磁界の大きさBzと電界の大きさEy の比については、空間に電流がないときには
という関係があるのですが、それを説明するためにはマックスウェル方程式の展開が必要になりますので割愛します。これを(3)式に代入すると、電界と磁界についてそれぞれ次の関係が得られます。
電磁波が進行するときにエネルギーが伝播するのですが、それは前回に引用したイギリスのH.J.Poyntingの理論によって計算できます。ここでは単位面積あたりを通過するエネルギー密度はEy Bz
よって座標系間のエネルギー密度の比は次式になります。
ただしβ=v/c
時間の短縮
図1において、静止している物体が時刻 t=0 t=
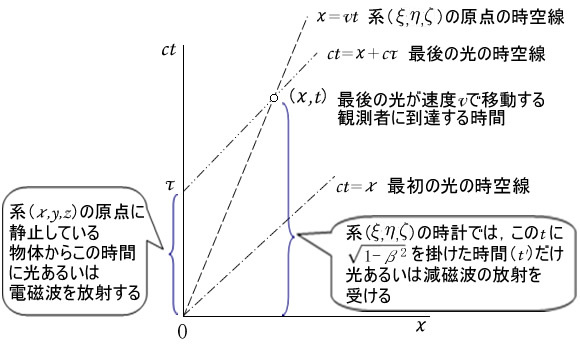
では、静止している人から見て、速度v (ではどうなるでしょうか。t=0 t= c このとき系(の原点は、x=v v で遠ざかります。最後の光がこの原点に到達する時間と位置は、図2 に描いた時空線の上で2つの直線の交点として計算すると
になります。しかし、系(においた時計では、この時間が短縮されるというのが相対性理論の面白さです。
図2 時空線での計算(「 ピタゴラスの定理でわかる相対性理論」p.148参照) その関係式こそ表の②のローレンツ変換でして、( の時計で測った時間は
です。( 7),(8)の関係をこれに入れると
が導かれます。
ちなみに、これと (7)式から
であることがわかります。つまり、速度v (で観測される時間 t 系(での当事者にとっては(相対性理論の読み物に出てくる双子のパラドックスはこれにまつわるお話だと思います) 。
図1で、系の原点に静止している物体が、光(あるいは電磁波)を放射した時間は(の時計では、その原点にある単位面を光が通過する時間はt'
さて、単位面を通過したエネルギーの全量はエネルギー密度と時間を掛けたものです。つまりエネルギー量の比率(l' l はエネルギー密度の比(P' P (t' を掛けたものですから
となります。これはまさに(2)式です。
9月論文の最後の一文をもう一度思い返してみましょう。
Wenn die Theorie den Tatsachen entspricht, so überträgt Strahlung Trägheit zwischen den emittierenden und absorbierenden Körpern.
もしこの理論が事実に対応すれば、放射は放出源の物体と吸収源の物体の間で慣性量を輸送するといえる。
これは光とは何だ? という問いへの一つの答だと、アインシュタインは考えたのかもしれません。つまり、物体が光を吸収したり、あるいは光を放ったりすることについて考えたのだろうと思います。では彼が何時そうことを考え始めたのでしょうか?
それは1900年に発表されたマックス・プランクの論文に記されている輻射(Stahlung)に関する重要な実験が起源だったと思われます。そしてアインシュタインは、1905年3月にノーベル賞の対象となった3月論文を発表しています。
アインシュタインは自分では実験をしなかったのですが、他の物理学者の実験結果から本質を汲み取る能力においては抜群でした。それを次回のテーマしようと思います。
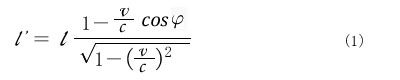
![]() )
)![]() )
)![]() )
)![]() )
)![]() の基本的な場合に限ってみたいと思います。つまり、
の基本的な場合に限ってみたいと思います。つまり、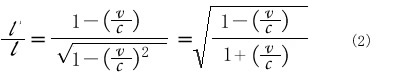
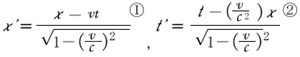
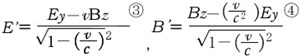
![]() のときには
のときには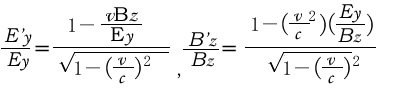
![]()
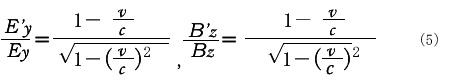
![]() です。つまり互いに直角の向きの電界Eyと磁界Bzを掛けあわせて真空の透磁率
です。つまり互いに直角の向きの電界Eyと磁界Bzを掛けあわせて真空の透磁率![]() で割ったものです。
で割ったものです。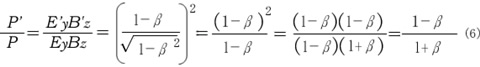
![]() まで(光あるいは電磁波の)平面波を放射したとします。
まで(光あるいは電磁波の)平面波を放射したとします。![]() )
)![]() で放射を終えたときの光が速度cで伝播するのですが、
で放射を終えたときの光が速度cで伝播するのですが、![]() )
)![]() の位置にあって速度vで遠ざかります。最後の光がこの原点に到達する時間と位置は、
の位置にあって速度vで遠ざかります。最後の光がこの原点に到達する時間と位置は、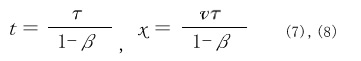
![]() )
)
![]() )
)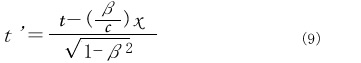
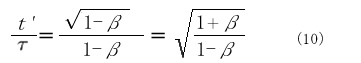
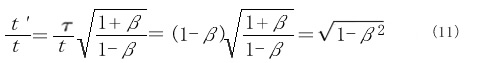
![]() )
)![]() )
)![]() だけ短縮されて
だけ短縮されて![]() になるのだといえます
になるのだといえます![]() です。この系では物体から離れていてもx軸と垂直な単位面(たとえば1cm2の面)を光が通過する時間も同じ
です。この系では物体から離れていてもx軸と垂直な単位面(たとえば1cm2の面)を光が通過する時間も同じ![]() です。しかし系
です。しかし系![]() )
)![]() )
)