c は光速度です。
(1)式ではE は電界強度の意味で使われるのですが、(3)式ではエネルギーです。
(3)式の左辺の-E 2 を右辺に符号を変えて移動し、右辺の-(m0c 2 ) 2 を符号を変えて左辺に移動すると次式がえられます。

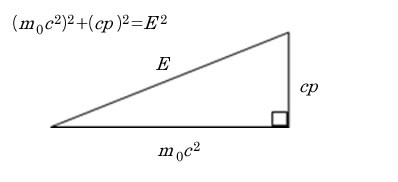
これは図1の直角三角形の関係になります。つまりピタゴラスの定理の式になります。
図1 運動量と静止エネルギーに関する直角三角形の関係
以降では左辺と右辺を入れ替えて

の形から再出発します。
『ピタゴラスの定理でわかる相対性理論』9.7 開けてしまったパンドラの箱のところに、相対性理論のエネルギーとして
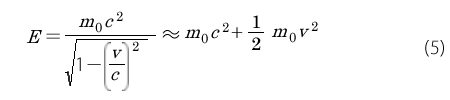
と書いています。ただし、m0 は静止質量です。この式は意味深長ですので、ここでもう一度証明しておきます。(4)'を変形します。
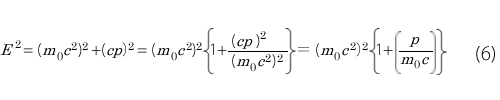
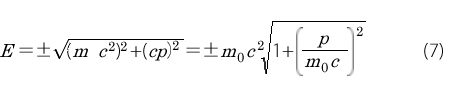
負のエネルギーについては考えないことにして、p がm0 に比べてずっと小さいものとしてコラム1を参照して次式を得ます。
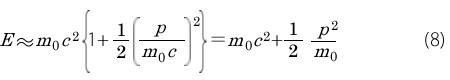
質点の場合にはp =m0v であるから先の(5)式になります。
粒子か波動かにをしっかり見よう
光が粒子なのか波動なのかという問題については、アインシュタインよりずっと前に議論されて、ヤングの実験によって波動だということで落ち着いていました。今でも電磁波は目に見えない光の類であるとして波動として解析されています。
ところが、光について考え抜いたアインシュタインは、粒子として最小の単位が光にもあるのだと提唱しました。これがアインシュタインのノーベル賞論文になったのですが、その論文は前回でに解説したように1905年のものです。
アインシュタインの一般相対性理論がイギリスの観測隊によって証明されたのが1915年です。それでも相対性理論については懐疑的な雰囲気があったのだろうと思います。この論文で論じた光電効果に対してノーベル賞が決定したのは日本に来る船に乗っているとき(1922年秋)のことでした。
(8)式を波動という観点で見ます。右辺の第1項は物質の静止エネルギーであって、これは波動ではないと解釈します。波動の成分だけを取り出すと

になるとしましょう。
波動現象を複素数で見てみよう
波動現象はsin(kx -ωt )あるいはcos(kx -ωt )を基本として語ることができます。両方を同時に表す方法として虚数iを取り込んで指数関数を使って次のようにします。
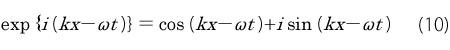
波動方程式というのは波動の本質的な性質を微分方程式の関係で表すものです。もっと具体的には時間t に関する微分と位置x の微分の間の関係式のことです。それについて考えるための準備として(10)式の時間微分と位置微分を見ましょう。
時間で微分すると
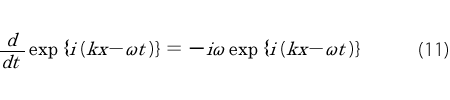
位置で微分すると
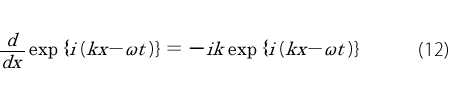
となります。
これらの形から形式的に


の関係が得られます。
このように虚数が現れる関係式は、いったいどんな意味を宿しているのでしょうか? この疑問を飛ばして先に進むことも、ここで説明をすることもできますがかえってゴタゴタしそうです。そこで形式的にどんどん進みます。そして後で振り返ってみてください。
アインシュタインが主張した光量子(フォトン)のエネルギーが、周波数 に比例することと(13)式を関連させられそうです。エネルギーのE を波動という枠の中で考えるときには時間微分(d/dt )に関係しそうです。
ここでv は周波数であるから角周波数ω で示すとω/2π ですから

です。
ここの(13)式の関係を形式的に入れて

とします。ここでは,フォトンのエネルギーと周波数の関係を電子にも適用してみようとする意味があります。
一方、ド・ブロイは運動量p は波数k に関係してhk/2π としました。運動量は位置の微分(d/dx )に関連しそうです。
ここには次の対応があるようです。
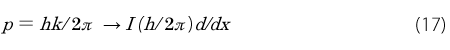

このようにして得た(16)と(18)式の関係を(9)式に代入すると
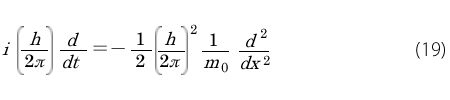
となりますが、両辺から(h/2π )を取り去って次式が得られます。
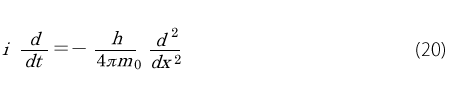
これは電子のどんな物理量に関する微分の関係なのか不明であるから、とりあえずΨ というものを演算の対象とします。このようにしてΨ に関する時間微分と位置微分の関係式として
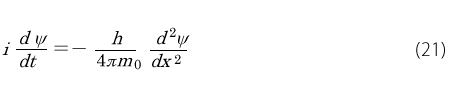
がえられます。これが有名なシュレディンガー方程式のもっとも簡単なものです。
複素数の意味を考える
(21)式が成り立つためには、とりあえずΨ は実数ではなく複素数でなくてはいけません。
さて、ここからが見城流の説になります。この複素数を実数部分ΨR と虚数部分iΨI に分けて次のように書いてみます。

これを(21)式に入れてみると次にようになります。
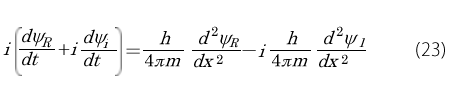
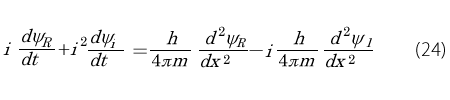
ここでi 2 =-1を思い出して次のようにします。
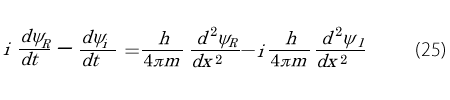
そして左辺を並べかえします。
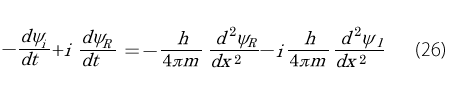
この式が成り立つためには、左右の実数部分と虚数部分がそれぞれが一致しなくてはいけませんので,次の2つの式が得られます。
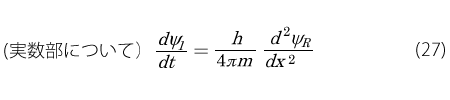
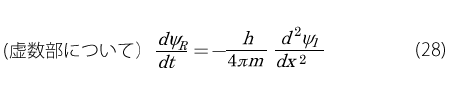
これは実数部分と虚数部分の関係だとも言えるのですが、そうではなく次のような論理としてもよいかと思います。
図2(a)に示しているように、電磁波の伝播においては磁界と電界が互いに作用しあっているように、電子の挙動も2つの要素の相互作用として解釈するために、ΨR とΨI を2つの要素としてが、互いに上の二つの方程式によって関係付けられるのだとするのです。
図2 電磁波と電子の波動
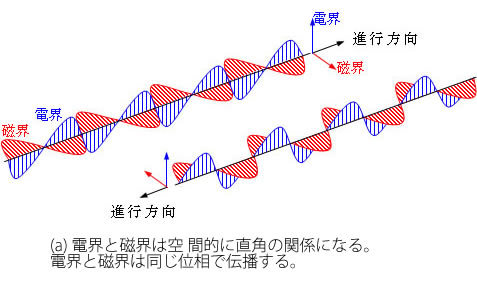
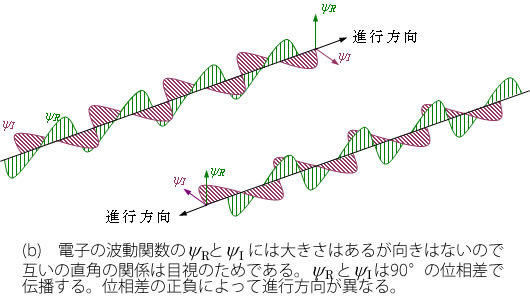 (a)のように電磁波では磁界(B )と電界(E )は同相の波動として進行する。一方、電子の波動では(b)に示すようにΨR とΨI は90°ちがいの波動として進行する。
(a)のように電磁波では磁界(B )と電界(E )は同相の波動として進行する。一方、電子の波動では(b)に示すようにΨR とΨI は90°ちがいの波動として進行する。
電磁界の場合には、コラムに示すような微分方程式の形になります。微分方程式というのは、それを解くという前に形の品評をします。左辺と右辺の関係に現れる不思議さや美しさに、こころが圧倒されます。時間t と位置x の微分とその階数の関係で、その波動の本質がすべて見えてくるのです。もちろんそれにはある程度の修行を必要とします。
さて、ここで上の2式からΨR あるいはΨI の一方を消去してみます。そのために(28)式の両辺を時間t で微分すると左辺は2階微分になるのですが右辺は次のようになります。
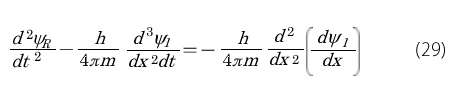
この右辺の()の中は(27)式ですから、これを代入するとx に関する4階微分が現れて次式になります。
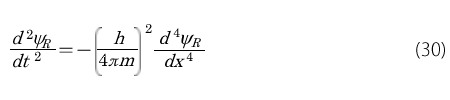
同じようにして次式も得られます。
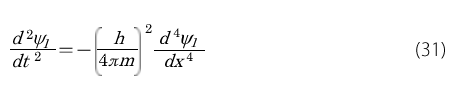
この式を見て、難しそうだなと思う人もいるかもしれません。そういうときには考え方を変えます。どこか参考事例がないかどうかを探します。するとあるのです。数学の先人の積み重ねは財産です。使うことによって、さらに大きな財産になります。
これは汽車のレールのように、弾性体の長い棒のようなものに伝播する機械的なたわみ波動の方程式と同じ形というか、その類の波動のなかのもっとも基本的な方程式であって、かなり研究されてきたものです。基本的には図3のように、長方形断面をもつ梁に伝播する上下運動と回転運動が相互作用する波動です。ちなみに、その方面に大きな足跡を残したのがチモシェンコです。
図3 梁(弾性体のレール)に伝わる波動
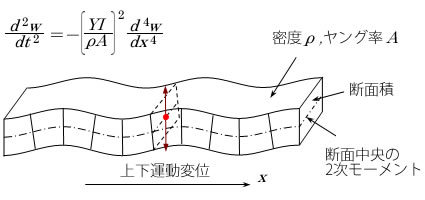 中央の各部分の上下運動wと回転運動が90°の位相差をもつ。
中央の各部分の上下運動wと回転運動が90°の位相差をもつ。
そういう古典的な解析から出てくる結果をうまく解釈すると、電子の波動が同時に粒子の様相を備えていることが簡単にわかってしまいます。それを示してみましょう。
この方程式の解はいろいろあるのですが、もっとも簡単なのは先にあげたような

として、このときにはΨI は

であって角周波数ω と波数k の関係が

になります。
シュレディンガーはΨ は、その絶対値の 乗和は電子がある特定の位置に存在する確率としました。絶対値の2乗とはΨR あるいはΨI のそれぞれの2乗の和です。
すると
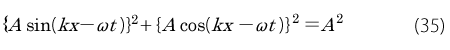
となって、波動の形sin(kx -ωt )は消えうせてしまいます。
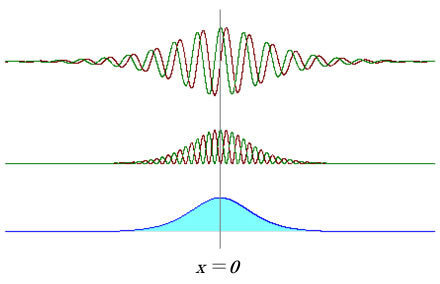
もっと現実的なのが、図4に説明しているよう波束の場合です。2乗和をとると電子が局所に存在することになります。つまり電子というものを2つの量の相互作用体と見たときには、それぞれの要素は波動の性質を具備しながら、存在確率は粒子の性質になります。
図4 (上)電子波の波束のΨR (緑)とΨI (茶)、(中)それぞれの2乗、(下)存在確率(2乗和)
 中央の各部分の上下運動wと回転運動が90°の位相差をもつ。
中央の各部分の上下運動wと回転運動が90°の位相差をもつ。
このように電子の存在確率の要素であるΨR とΨI は波動の様相を示すが、存在確率そのものには下段のように波の様子がなくなって粒子のようになる事例である。
ところが,特別の仕掛けをすると存在確率も波動になります。それは1個の電子が同時に2つの穴を通って自己自身と干渉して縞模様を見せてくれるという有名な実験です。そのコンセプトを示すのが図5です。ここでは詳しい説明をしていませんが、1個のある特定の電子が今どこに存在するかの問題がしばしば議論されます。
図5 電子は同時に同じ穴を抜けて、スクリーンに干渉縞を描く
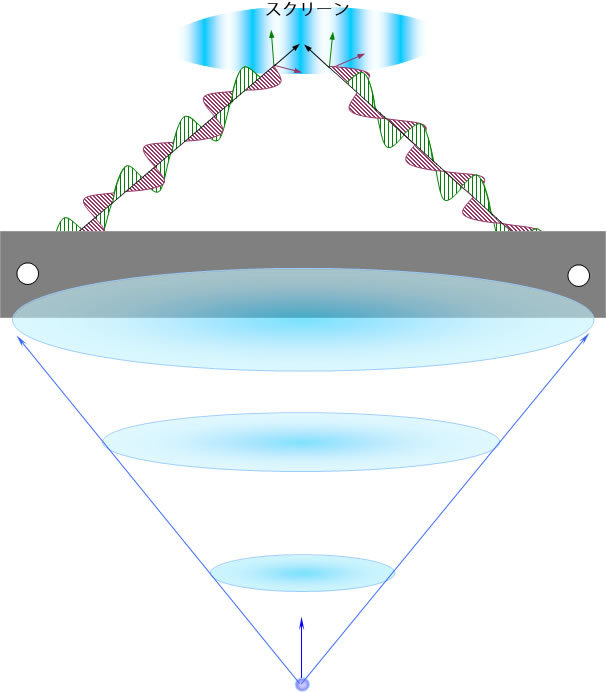 中央の各部分の上下運動wと回転運動が90°の位相差をもつ。発射される電子:空間的な広がりをもって進行し、同時に二つの穴を通るときに回折してスクリーンに自己干渉して縞模様が現れる。
中央の各部分の上下運動wと回転運動が90°の位相差をもつ。発射される電子:空間的な広がりをもって進行し、同時に二つの穴を通るときに回折してスクリーンに自己干渉して縞模様が現れる。
ニュートン力学では、質点といって大きさの無い点で規定して数学的には(x,y,z )の座標で示します。ところが波動力学(量子力学)では、粒子の存在する位置は特定の質点でなく広がりをもつとされます。その広がりの領域は状況によって違います。電子1個が何かによって放出されて加速されたとしても、厳密な線のような経路を通るとは限りません。むしろ広がりをもつと考えます。すると1個の電子が同時に異なる穴を通ることが否定できません。そして回折によって図に描くような自己干渉が起きます。
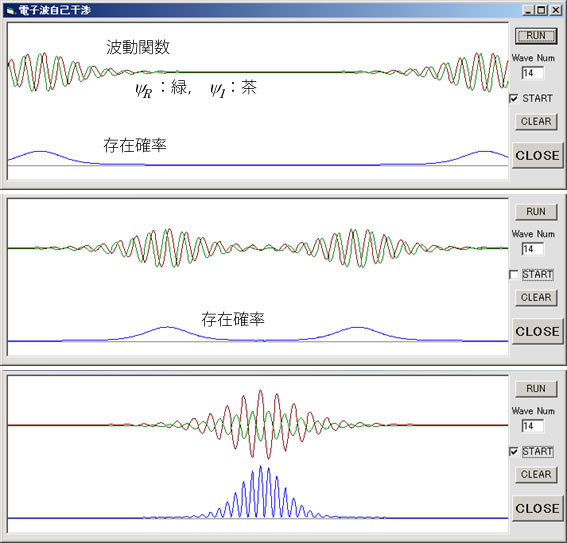
図6は、本質的なところをアニメーション化したソフトウェアです。左の穴を通った回折波と右の穴を通った回折波のそれぞれは粒子のような存在確率を示すのですが、重なって干渉すると存在確率に濃淡が現れます。つまり縞模様がスクリーンに現れることを意味します。
図6 自己干渉して存在確率が縞模様を描く様子を示すアニメーション。左の穴を抜けて回折した波動と右の穴を抜けて回折した波動が重なるときに存在確率が縞模様になる。つまり波動特有の干渉縞だと解釈される。
- 操作手順
- RUNをクリックするとこの画面が現れる。
- STARTの
 をはずすと波束が左右から中央に向かって進行する。位相速度は波束の進行速度の1/2である。
をはずすと波束が左右から中央に向かって進行する。位相速度は波束の進行速度の1/2である。
- 2つの波束が重なると存在確率が波状(濃度で見ると縞模様)になる。[START]をキックすると停止する。
- 波数(Wave Num)は適当に変えてよい。
- 再度実行するときには[CLEAR]ボタンをクリックします。
- プログラムを終了するときには必ず[CLOSE]ボタンをクリックしてください。この操作をしないでPCを閉じると、この計算ブログラムがPC内部に残り続けます。
- 自己干渉して存在確率が縞模様を描く様子を示すアニメーションソフト
光電効果とはこういうことか? そしてあとがき
以上を総括したのが図7です。光電効果の様子です。原子核に束縛されている電子が光子からエネルギーをもらうのですが、光子は弦に伝播する波動のような振る舞いをしています。これからエネルギーをもらって電子が外に飛び出すときの波動としての性質は梁やレールに伝播する波動のような振る舞いをします。このあたりのメカニズムはわかりません。モデルを工学的に作ってみるのは面白そうですが、どんな仕掛けが考えられそうでしょうか? アインシュタインは1905年の論文で、頻繁にResonator(共鳴子)という単語を使っています。共鳴とは特定の周波数で楽器の弦が震えるようなものです。
図7 光電効果とはこういうことか?
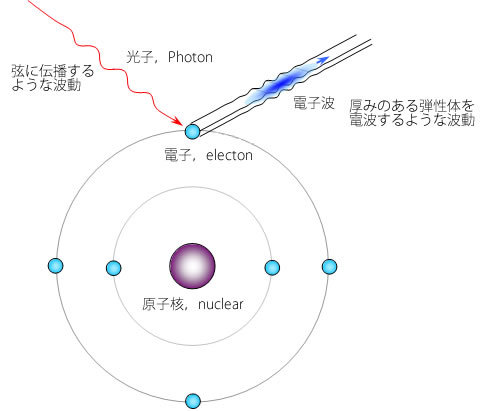
アインシュタインがこの問題を考えていた当時は、電子は小さなこの図に描いたような粒子と考えられていたのですが、その後になって空間的な広がりをもつと考えられるようになり雲(cloud)のようなモデルで論じられることもあります。ところが、この電子が光子を捉えてエネルギーを奪うのですから、蜘蛛(spider)の巣のようなモデルを想像することだったできそうです。
この仕掛けが、(4)式のピタゴラスの定理の形に宿されているのかもしれません。ここでは光子のように質量が0の波動と、電子のように質量があってそれほど速くない速度で移動する物体の波動を手品のようにして描きだしてみました。数学的な近似を使っています。そのためもあるのか、(20),(22),(23)の各式はローレンツ共変になっていないのです。つまり、アインシュタインの相対性理論の条件を満たさないのです。寺院のタイルに宿される秘儀は汲みつくすことができません。
その問題に深く切り込んだのが、イギリス生まれのディラックでした。(彼は、先の(7)式に現れる負のエネルギーについても考察してします。)これが湯川秀樹による素粒子理論へと発展したのです。次回はこのあたりを見てみようと思います。
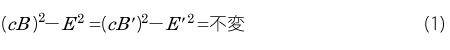
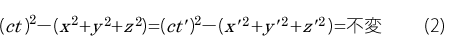




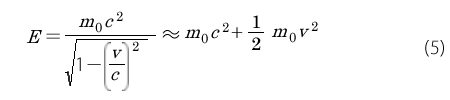
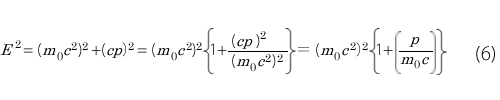
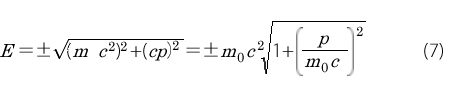
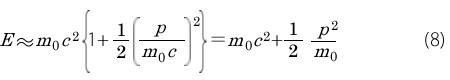

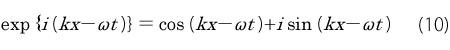
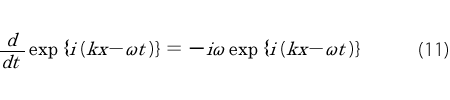
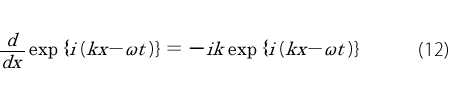




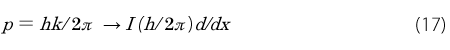

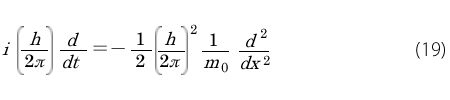
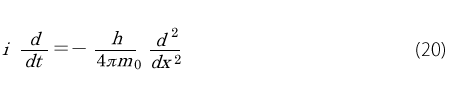
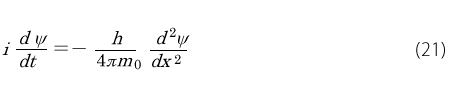

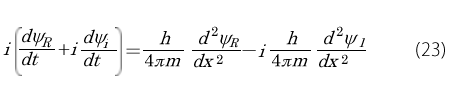
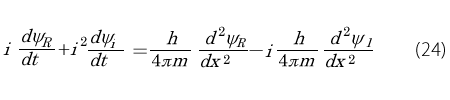
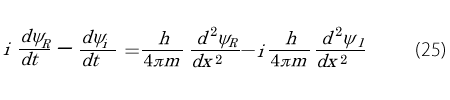
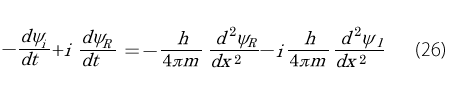
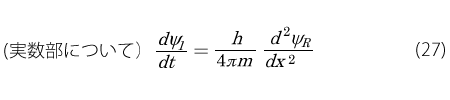
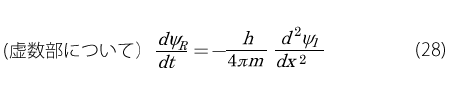


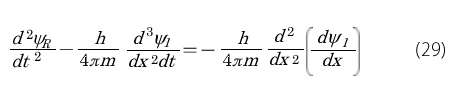
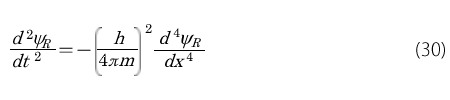
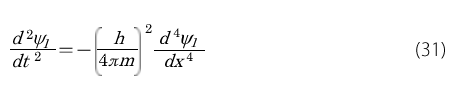




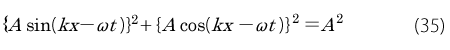



![]() をはずすと波束が左右から中央に向かって進行する。位相速度は波束の進行速度の1/
をはずすと波束が左右から中央に向かって進行する。位相速度は波束の進行速度の1/


