はじめに
今回からは、2つの凸多角形を重ね合わせて、その共通部分を切り出す交差計算を見ていきます。以前に学んだ平面走査法をうまく応用することで、高速な交差計算が可能になります。また、この凸多角形の交差計算は、本連載の最後で取り上げるボロノイ図の作成にも深く関係します。
図形のブーリアン演算
Adobe Illustratorなどのドローツールでは、2つの図形を結合して新しい図形を作り出す操作が良く行われます。これはブーリアン演算(boolean operation)と呼ばれ、領域を併合するunion演算、共通部分を切り出すintersection演算、差分を求めるdifference演算といったバリエーションがあります(図1)。
図1 ブーリアン演算
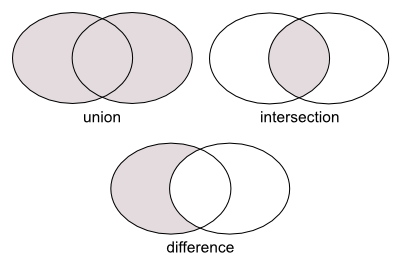
一般に、図形のブーリアン演算は複雑な処理になります。多角形同士の演算を考えてみても、図2に示すように、演算結果が「穴」を含む領域になったり、分離した領域になったりするため、もはや結果を単純な頂点配列などで表現することはできず、二重辺連結リスト(doubly connected edge list)などのデータ構造が必要になります。
図2 一般のブーリアン演算
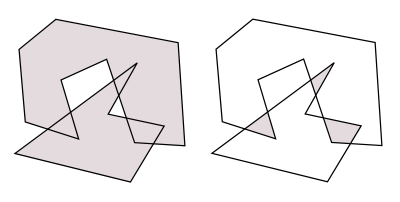
しかし、凸多角形同士のintersection演算、すなわち交差領域の計算に限れば、処理はいくぶん簡単にです。なぜなら、2つの凸多角形の共通領域の形状は、必ず凸多角形になるというシンプルな性質があるからです(図3)。
図3 凸多角形同士の交差
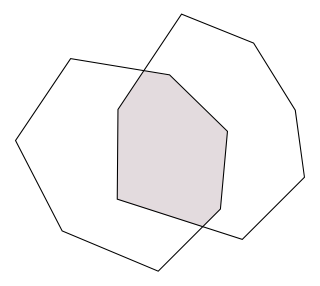
今回からは、前回までに作成したConvexPolygonクラスをもとに、2つのConvexPolygonオブジェクトから新しいConvexPolygonオブジェクトを作り出す交差計算の方法を解説していきます。
解説の方針
これまでの回では、説明した内容に対応するソースコードを、その都度紙面に掲載するスタイルで記事を構成してきました。しかし、今回はソースコードの規模がやや大きくなるため、ページにプログラムを含めると、解説文が冗長になってしまいます。
そこで、今回以降の連載では、アルゴリズムの大まかな流れを示すにとどめたいと思います。もちろん、最後にはソースコードのアーカイブファイルを公開しますので、興味のある方はぜひダウンロードして、実装の詳細を確認してみてください。
平面走査法の応用
2つの凸多角形の交差から作り出される新しい凸多角形は、どんな頂点から構成されるでしょうか。図4からも容易に分かるように、それは元の2つの凸多角形のいずれかの頂点になるか、あるいは元の辺同士の交点になります。
図4 交差計算結果の頂点
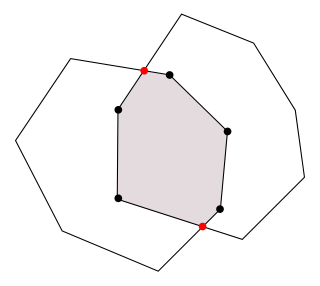
つまり、凸多角形の交差計算の過程には、凸多角形が持つ辺の中から交差を見つけ出す処理が含まれることになります。したがってこれには、第3回から第5回にかけて学習した、平面走査法による線分の交差検出のアプローチを応用できることになります。
簡単に復習しておきましょう。平面走査法では、平面領域上に仮想的な走査線を設定し、イベント点を単位として、走査線が領域を離散的に通過するようになっていました。走査線の移動は、イベントキューから次のイベントを取り出すことによって行われます。また、現在の走査線と交わる線分は、ステータスと呼ばれるデータ構造に格納されます。
以下、凸多角形の交差計算においては、ステータスとイベントキューをどのように表現するのが最も合理的かを考えていきましょう。
凸多角形の交差計算におけるステータス
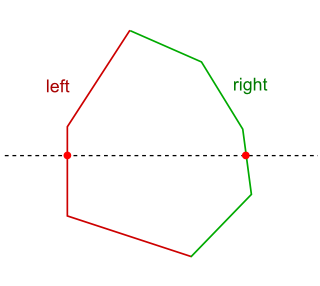
線分の交差検出の場合、ステータスには順序付き集合が使われました。しかし、凸多角形の交差計算では、ステータスにはもっとシンプルな構造を用いることができます。なぜなら、1つの凸多角形が走査線と交わるとき、その交差は図5に示すように、たかだか、凸多角形の「左側」にある辺と「右側」にある辺の2つに限定されるからです。計算の入力となるのは2つの凸多角形ですから、走査線と交わる線分の数は、最大でも4つにしかなりません。
図5 凸多角形と走査線の交差回数
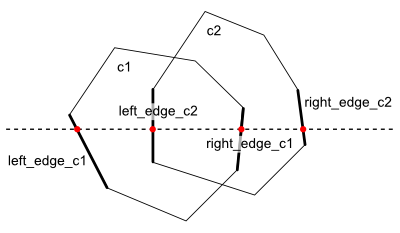
入力の凸多角形をc1, c2とすると、c1の「左側」の辺を指すポインタleft_edge_c1、「右側」の辺を指すポインタright_edge_c1を用意し、さらにc2についても同様にleft_edge_c2とright_edge_c2を用意すれば、この4つのポインタだけでステータスを表現できることになります(図6)。
図6 4個のポインタによるステータスの表現
順序付き集合の操作には、log(n)のオーダーで計算時間がかかっていました。これに対して、4個のポインタを使った場合、ステータスの計算は定数時間で実行できてしまうため、速度面でも有利になります。
凸多角形の交差計算におけるイベントキュー
次に、イベントキューについて考えます。線分の交差検出では、計算途中で交点イベントが動的に生成されるため、キューに対するイベントの追加や取り出しの操作を高速に実行できるよう、ステータスと同様に順序付き集合が使われました。
これに対して、凸多角形の交差計算ではイベントの考え方がやや異なり、交点イベントは用いません。したがって、走査線が移動すべき次のイベント位置を求めるには、left_edge_c1, right_edge_c1, left_edge_c2, right_edge_c2の各下端点のうち、もっとも上に存在する点を調べれば十分です。イベントキューの存在意義は、次に処理するイベント点を見つけることなので、凸多角形の交差計算では、イベントキューをわざわざ用意する必要がないのです。
もう少し詳しく述べると、平面走査法による凸多角形の交差計算において、走査線を次の位置に移動させる処理は、以下のように実行することができます。
- 1.辺ポインタleft_edge_c1, right_edge_c1, left_edge_c2, right_edge_c2の中から、下の端点がもっとも上に存在するものを選ぶ。
- 2.選択された辺ポインタを、その下端点に接続する次の辺を指すように更新する。
このように、凸多角形の交差計算における平面走査法ではイベントキューを使わないことから、イベントキューの操作に必要だったlog(n)の計算時間も削減できることになります。
まとめと次回予告
今回は、図形のブーリアン演算の中でも比較的容易に実装することのできる、凸多角形の交差計算を紹介しました。また、この計算には線分の交差検出の際に用いた平面走査法が応用できることを示し、線分の交差検出に比べ、ステータスやイベントキューがより単純なデータ構造で表現できることを説明しました。
次回は、平面走査法を使った凸多角形の交差計算において、イベントが発生したときどのような処理を行えば良いかを見ていきます。お楽しみに!









