材木を寸法ぴったりの長さに切り取りたいとき、どんな作業をするか考えてみましょう。先ずは目標の寸法のところに印を付けます。次に印が消えない程度に、少し長めにのこぎりで切り落とします。次にかんなをかけて端面を仕上げます。通常はこれで十分ですが、更に目標寸法へ追い込みたい場合はヤスリをかけます。少しずつ、少しずつ目標の寸法に近づけていくわけです。少々の隙間は良しとしたり、1mm単位で寸法を決めたり、より精度良く仕上げる場合には10分の1mm程度まで追い込んだり。現在の仕事に必要十分なところで寸法精度への要求を打ち切ります。要は必要な仕事をできるだけ効率よく行えばよいのです。
プログラミング言語の実数型を用いた計算も、同じような考え方を必要とします。こちらは選択した型によって要求できる精度が決まりますから、あとはプログラマが上手にその精度を利用する必要があります。必要以上に高い精度で計算することは無駄ですし、必要な精度で計算できなければ仕事になりません。これは言ってみれば妥協をするのではなく、見切りを付けると言うことです。今回は実数型のそんな側面について学びます。
図13.1 必要な精度内で無駄なく仕事
浮動小数点数で発生するエラーや誤差
浮動小数点数の仕組み上避けられないエラーや誤差には次に挙げるものがあります。
オーバーフロー/アンダーフロー
桁落ち
丸め誤差
情報欠落
打ち切り誤差
今回は最後の「打ち切り誤差」を学習しましょう。
打ち切り誤差
円周率や自然対数の底、コンピュータの数値表現の制約や実用上、通常ある精度で計算を打ち切らなければならなりません。このため計算結果は真の値とは異なります。こうした事情で発生する誤差を打ち切り誤差 といいます。誤差を含む数値で各種の演算を重ねると、その結果大きな誤差が生じる危険があります。極端な例では、円周率の値を3とした場合と、3.1415とした場合では約5%の誤差が発生します。この5%の誤差が大したことでない場合もありますし、大変な場合もあります。プログラマはその状況に応じた精度で計算できるプログラムを作らなければなりません。
それならば、いっそのことより高い精度で計算しておけば良いのでは?と思うのは自然なことですが、高い精度で計算するためにはコンピュータの計算資源を余分に必要とします。できることなら、工夫なしに現在発揮できる精度いっぱいの計算をして、そこで打ち切るのが無駄のない選択肢だといえます。
打ち切り誤差は、これまでに学習した4つの誤差に比べると、プログラマの側の働きかけによって決定する部分があるので、少々ポジティブな誤差だと言えます。ポジティブだろうがネガティブだろうが、そこに誤差があるわけですから、計算を行う我々プログラマは誤差の発生理由と程度を理解しておきましょう。
それではここで、自然対数の底e (ネイピア数 という)の算出を例に取り上げてみます。ネイピア数は次のように定義されています。
この定義式でx=1として、nを無限に増加させていけば、限りなく真の値に近づきます。しかし、コンピュータを用いた数値計算では、精度は計算結果を格納する変数に依存します。何度繰り返して計算しても、値に変化が現れないようでは計算を続ける意味がありません。
仮に計算結果を格納する浮動小数点数型の変数に十分な余裕があるとしましょう。しかし計算にかかる時間が長くなるのであれば、その時間をかけても計算する意味のあるところまでで打ち切るべきでしょう。数千回、数万回と繰り返す必要のある計算の場合はコンピュータを長時間占有することになります。時は金なりと言います。その問題は、時間とお金をどんどん積み上げても計算する必要があるでしょうか? コンピュータを用いた数値計算では、合理的で妥当なところで計算を打ち切ります。計算を打ち切ったところで相応の誤差を含むことになるのです。
それでは、実際にfloat型の精度いっぱいまで計算してみましょう。
問題:ネイピア数の定義に従い、float型の最大精度で計算し、結果を出力しましょう。
ネイピア数eは次の式で定義されます。
ただし、x=1です。
(1)
(2) 何個目の項を加算したところでfloat型の精度いっぱいの値になるか確認しましょう。
解説
(1) 式に忠実にソースコードを作成すると、無限に加算を繰り返すことになります。しかし、現実的にそれは無理ですから計算に意味のあるところまで繰り返すことにします。計算に意味がなくなるのは、ある時点の計算結果と次の時点の計算結果が同じであるという条件にしてみました。無限ループになっては困るので、繰り返し回数はint型の最大値までとしました。以下にそのソースコードを示します。
1:
2:
3:
4:
5:
6:
7:
8:
9:
10:
11:
12:
13:
14:
15:
16:
17:
18:
19:
20:
//filename : Uchikiri_Gosa.java
class Uchikiri_Gosa {
public static void main(String[] args) {
int i; //counter
float neip=0; //ネイピア数
float prev_neip=0;//一つ前に計算したネイピア数
float kaijyo=1; //階乗値の保管
for (i=0; i < Integer.MAX_VALUE; i++){
neip = neip + 1/kaijyo;
if (prev_neip == neip){
System.out.println(" final neip is " + neip);
System.out.println("done...");
break;
}
kaijyo = kaijyo * (i+1);
System.out.println(i + " neip is " + neip);
prev_neip = neip;
}
}
}
(2) 何個目の項を加算したところでfloat型の精度いっぱいの値になるか確認しましょう。 実行結果を次に示します。
Uchikiri_Gosa.java の実行結果
0 neip is 1.0
1 neip is 2.0
2 neip is 2.5
3 neip is 2.6666667
4 neip is 2.7083335
5 neip is 2.716667
6 neip is 2.7180557
7 neip is 2.718254
8 neip is 2.718279
9 neip is 2.7182817
10 neip is 2.718282
final neip is 2.718282
done...以上の実行結果から、n=10で精度いっぱいの結果を得たことがわかりました。ネイピア数は2.7182818284・・・ですから、8桁目を四捨五入したと考えれば7桁目まで正確な値を得たと言えます。
n=0から計算を開始しましたから、11項めの加算で終了したのです。12項めは000000025です。左から9桁目にやっと0以外の数値が現れます。n=0の時の第1項めは各項の値は常に正ですから、仮に小数点以上の値がひと桁であってもn=11で必ず加算の際に情報欠落を起こします。これ以上加算を継続する意味がないことがあらかじめわかります。
このように、あらかじめnを適当に選んで計算してみることで、おおよそ何回目で計算が終了するか予想することができます。数値計算に当たっては、プログラムの実行前に計算回数を見立てるよう心がけましょう。それが無駄のない仕事をするために役立ちます。
今回のまとめ
実数型で桁数の多い数値を計算する場合、保管できる桁数に限りがあります。その時に格納できる桁数以上の計算を行っても意味がありません。この見切りの結果発生するのが打ち切り誤差です。

![]() などの無限小数値の値を求めたい場合、
などの無限小数値の値を求めたい場合、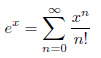
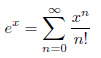
![]() =0.
=0.![]() =1、
=1、


