柔道の技には左右があります。右利きの人は右技ばかりを稽古すればよいかというと、
今回学ぶ正方行列は、
正方行列
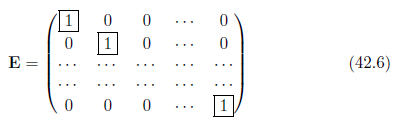
行列の行の数と列の数が同じ場合、
行数がnのとき、
以下に2次から4次の正方行列の例を示します。

対角行列
n次の正方行列において、

正方行列のうち、

単位行列
対角行列のうち、
転置行列
行列の行と列を入れ替えたものを転置行列
行列![]() の転置行列は
の転置行列は![]() と書きます。
と書きます。
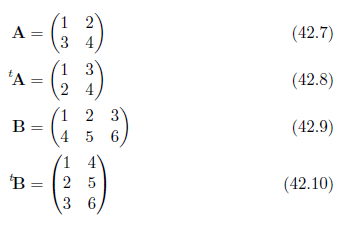
特に、![]() =
=![]() が成り立つ正方行列
が成り立つ正方行列![]() のことを対称行列
のことを対称行列![]() =
=![]() が成り立つ正方行列を交代行列
が成り立つ正方行列を交代行列
対角成分以外の値がゼロである対角行列は、
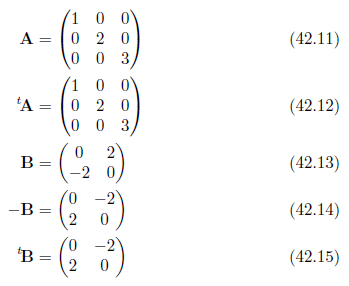
問題 以下に示す関数を作りましょう。
以下にそれぞれの問題に取り組むためのソースコードを掲載します。不足するコードを補って完成させましょう。ソースはテストの形をとっており、
//サンプルコード
//引数に与えた行列が正方行列か判定する関数。配列版。
//filename : Sample_isSquareMatrix.java
class Sample_isSquareMatrix {
public static void main(String[] args) {
int a[][] = //行列A 3x3
{ { 3, 4, 5 },
{ 6, 7, 8 },
{ 9,10,11 } };
int b[][] = //行列B 3x2
{ { 9,10 },
{ 11,12 },
{ 13,14 } };
int c[][] = //行列C 4x2
{ { 9,10 },
{ 11,12 },
{ 13,14 },
{ 15,16 } };
//正方行列でしょうか?
System.out.println("Test Start");
test_isSquareMatrix(a,"a",true);
test_isSquareMatrix(a,"a’",false);
test_isSquareMatrix(b,"b",false);
test_isSquareMatrix(c,"c",false);
System.out.println("Test Done");
}// end of main
/*
* test_isSquareMatrix
* 目的: isSquareMatrix メソッドのテスト
* 引数: m[][] 判定する行列
* valName 引数に渡した行列の変数名
* RoH(Result of Hope) 期待される結果
*/
static boolean test_isSquareMatrix(int m[][],String valName,boolean RoH){
if (isSquareMatrix(m) == RoH) {
return true;
} else {
System.out.println(valName + "のテストは目的の結果になりませんでした。");
return false;
}
}
/*
* isSquareMatrix
* 目的:引数に与えた行列を表す配列が、正方行列かどうか判定する。
* 行数と一行に入っている要素数が等しいか確認する。
* 引数: m[][] 判定する行列を表す整数型の二次元配列
* 戻り値: boolean 正方行列なら真
*/
static boolean isSquareMatrix(int m[][]){
// ここから 目的のコードを加えましょう。
//
// ここまで
}
}// end of class Sample_isSquareMatrix//サンプルコード
//引数に与えた行列が対角行列か判定する関数。配列版。
//filename : Sample_isDiagonalMatrix.java
class Sample_isDiagonalMatrix {
public static void main(String[] args) {
int a[][] = //行列A 3x3
{ { 3, 4, 5 },
{ 6, 7, 8 },
{ 9,10,11 } };
int b[][] = //行列B 3x2
{ { 9,10 },
{ 11,12 },
{ 13,14 } };
int c[][] = //行列C 4x2
{ { 9,10 },
{ 11,12 },
{ 13,14 },
{ 15,16 } };
int d[][] = //行列C 3x3 の対角行列
{ { 1, 0, 0 },
{ 0, 2, 0 },
{ 0, 0, 3 } };
int zero[][] = //行列Zero 3x3 の零行列
{ { 0, 0, 0 },
{ 0, 0, 0 },
{ 0, 0, 0 } };
//対角行列でしょうか?
System.out.println("Test Start");
test_isDiagonalMatrix(a,"a",false);
test_isDiagonalMatrix(b,"b",false);
test_isDiagonalMatrix(c,"c",false);
test_isDiagonalMatrix(d,"d",true);
test_isDiagonalMatrix(d,"d’",false);
test_isDiagonalMatrix(zero,"zero",false);
System.out.println("Test Done");
}// end of main
/*
* test_isDiagonalMatrix
* 目的: isSquareMatrix メソッドのテスト
*/
static boolean test_isDiagonalMatrix(int m[][],String valName,boolean RoH){
if (isDiagonalMatrix(m) == RoH) {
return true;
} else {
System.out.println(valName + "のテストは目的の結果になりませんでした。");
return false;
}
}
/*
* isSquareMatrix
* 目的:引数に与えた行列を表す配列が、正方行列かどうか判定する。
* 行数と一行に入っている要素数が等しいか確認する。
* 引数: m[][] 判定する行列を表す整数型の二次元配列
* 戻り値: boolean 正方行列なら真
*/
static boolean isSquareMatrix(int m[][]){
//このメソッドは前問(1) の結果を利用してください。
//対角行列の確認には、正方行列かどうかのチェックも必要です。
}
/*
* isDiagonalMatrix
* 目的:引数に与えた行列を表す配列が、対角行列かどうか判定する。
* 引数: m[][] 判定する行列を表す整数型の二次元配列
* 戻り値: boolean 対角行列なら真
*/
static boolean isDiagonalMatrix(int m[][]){
// ここから 目的のコードを加えましょう。
//
// ここまで
}
}// end of class Sample_isDiagonalMatrix解説
以下に、
(1)与えられた行列が正方行列かどうか判定する関数。
/*
* isSquareMatrix
* 目的:引数に与えた行列を表す配列が、正方行列かどうか判定する。
* 行数と一行に入っている要素数が等しいか確認する。
* 引数: m[][] 判定する行列を表す整数型の二次元配列
* 戻り値: boolean 正方行列なら真
*/
static boolean isSquareMatrix(int m[][]){
int row = m.length; //行数取得
int cul = m[0].length; //一行目の要素数(列数)の取得
boolean result = true;
if (row == cul) {
for (int i = 0 ; i (2) 与えられた行列が対角行列かどうか判定する関数。
/*
* isDiagonalMatrix
* 目的:引数に与えた行列を表す配列が、対角行列かどうか判定する。
* 引数: m[][] 判定する行列を表す整数型の二次元配列
* 戻り値: boolean 対角行列なら真
*/
static boolean isDiagonalMatrix(int m[][]){
boolean result = true;
if ( isSquareMatrix(m) ) { // 先ず正方行列であること
int row = m.length; //行数取得
int cul = m[0].length; //一行目の要素数(列数)の取得
for (int i = 0 ; i 今回はここまで
次回学習する逆行列、



