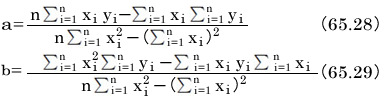前回は相関係数を導く準備として、統計の数学を用いて回帰直線の式を導きました。今回は前回で準備した要素をもとに、最終的に相関係数を導きます。どうして相関係数というものが登場したかがわかる、小説に例えれば主人公の登場秘話のクライマックスといったところでしょうか。
決定係数
回帰直線の一次式の定数が求まりましたから、回帰直線の式と測定値の間の関係の強さを評価する方法が欲しくなりました。そこで、回帰直線の式によって得られた値の分散と、測定値の分散が近ければ、関係が強いと評価することにします。そのような式を導き出してみましょう。
測定値の集合に、最も良くあてはまる回帰直線が得られたとして、各xi に対応するyの値を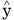 (推定値)と書くことにします。
(推定値)と書くことにします。

(65.1)-(64.27)

ここで、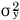 を見てみましょう。
を見てみましょう。
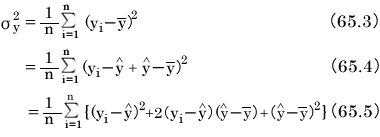
この式の総和部分の第2項は式65.2を代入して推定値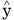 を消去できます。
を消去できます。
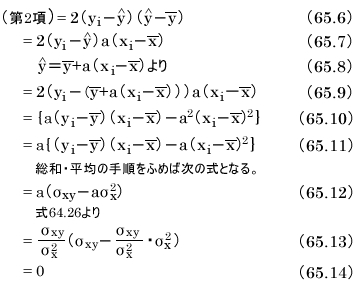
こうして、式65.5の第2項は0となることがわかりました。
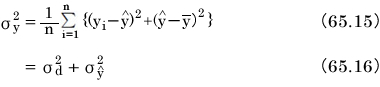
式65.16から、誤差の分散が小さければ、測定値の分散と推定値の分散が近くなることがわかります。
次の式を直線のあてはまり具合を表す目安として利用できると言うことが出来ます。

式65.17のR2 が1に近づくほど直線のあてはまりが良いといえます。このR2 を決定係数と呼びます。
相関係数
R2 には推定値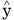 が含まれるので、これを取り除きたいと思います。そうすれば、実際に決定係数を計算するときの手間が減るからです。
が含まれるので、これを取り除きたいと思います。そうすれば、実際に決定係数を計算するときの手間が減るからです。
式65.16より、

(65.19)→(65.17)
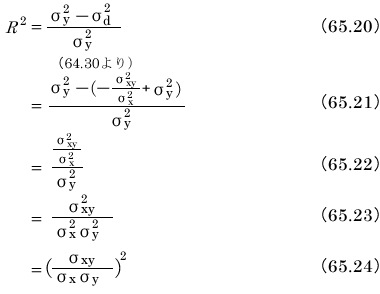
ここで、式65.24の平方根(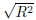 )を相関係数(r)と名付けます。
)を相関係数(r)と名付けます。

相関係数の利点
式65.27や図65.1に示すように、相関係数は-1から1の範囲の値を取ります。R が0から1であるのに対して広い範囲で表現できることに加えて、変化が直線的になりますので直感的に差を読み取りやすくなります。
図65.1 二次式と一次式の変化の読み取りやすさの差
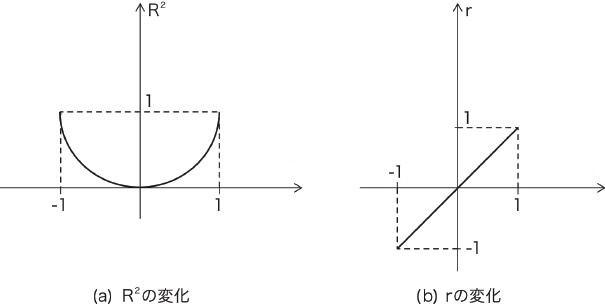
図65.1の(a)はR2 のグラフです。R の変化に対してR2 は、ゼロに近いところでは緩やかで、ゼロから離れるほど急になります。これに対して(b)は、当然ながら変化は直線的です。r の正負が回帰直線の傾きの正負を表してることもうれしいところです。
ただし、回帰直線の傾きについては、これまでの筋書きから考えると、既に最小二乗法で得た定数から知ることが出来るので、必ずしも重要とは言えないでしょう。
しかし、一般的に統計的にデータを処理しようとする場合、最小二乗法で回帰直線を近似する前に、散布図を作成し、先ず人の目でデータの性格を大まかに判断します。「お、これは、もしかしたら直線的な性質があるんじゃないか?」というところで、相関係数を求めて、最小二乗法を実施する意味があるかどうか判断する、という筋書きで使うことになるでしょう。そうなると、相関係数の正負で直線の傾きが読み取れるのは便利です。しかし、その場合にもグラフを見ているのなら、もう傾きの正負はわかりそうなもの。
やっぱり、相関係数が正負の値を取ることの実際の効用は、値の範囲が大きいことが一番でしょう。
問題 連載第60回で紹介した偏微分で求めた最小二乗法の定数の式と、今回紹介した統計的に求めた最小二乗法の定数の式が一致することを確かめましょう。
連載第60回で求めた式は次の2つの式です。
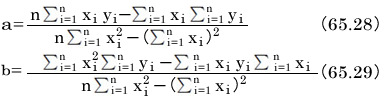
今回統計の数学を用いて求めた式は、aが式64.26、bが式64.29です。全く異なる手順で求められたこれらの式は、一致しているのでしょうか。今回は、aについてだけ一致するかどうかを確認してください。
解説
式64.26を展開します。

式65.36は確かに式65.28と一致しました。
bについても、時間を見つけて同様に確認してみると、統計の数学の各項目のよい復習となります。
今回の問題によって、統計の数学によって得られた最小二乗法の定数を求める式と、偏微分方程式を解くことで求められた式が一致することを確認できました。視点を変えると、偏微分方程式から導いた式は、統計の数学から導いた式を整理して単純化したものと見ることが出来ます。定義式としては、統計の数学で得た式(64.26,64.29)の方がすっきりしています。しかし、実際にデータを代入して計算する場合には、偏微分方程式から求めた式(65.28,65.29)の方が計算量が少なくなります。
私たちは、なにがしかの数値を計算しようとする際、教科書に登場する「人間にとって読みやすい・わかりやすい」かたちの式でコンピュータに計算させたくなります。もちろんそれは間違ったことではありません。バグを防止したり、計算結果の検証をするために有効です。しかし、計算の効率まで考えると、視点を変え、より単純な計算式になるのではないか?と疑ってかかることが大切になります。結局、今回の場合もそうですが、式が単純になるのですから、プログラムのバグも減り、検証も簡単になるのです。
今回はここまで
以上で統計の数学を終了といたします。本来ならば、検定[1]を学習すべきところです。しかし、検定は非常に広範な内容であり、ここで取り扱うには少々重すぎると判断しました。必要に応じて、専門書にあたり学習してください。これまでの内容をご自分でおさらいできるならば、十分独学が可能でしょう。必要に応じてチャレンジしてください。
![]()
![]()
![]()
![]() を見てみましょう。
を見てみましょう。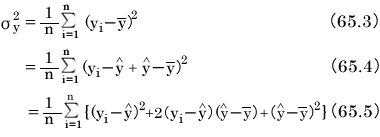
![]() を消去できます。
を消去できます。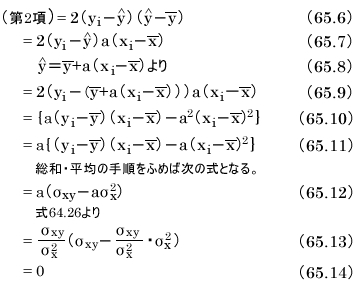
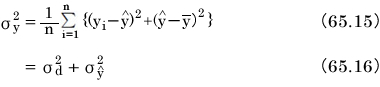

![]() が含まれるので、
が含まれるので、
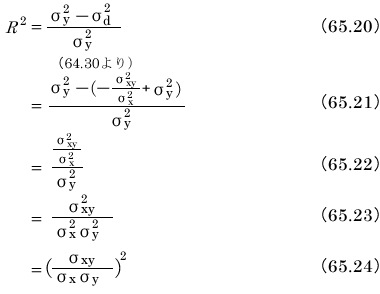
![]() )
)