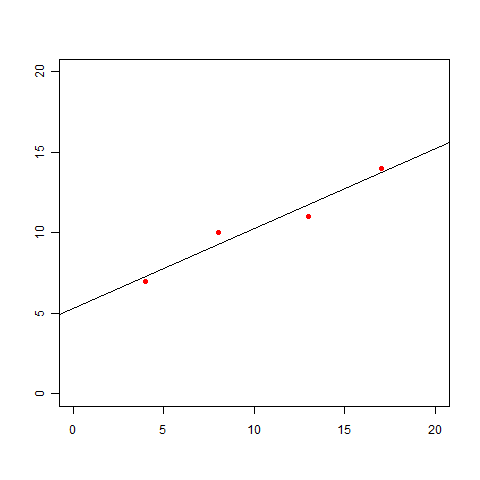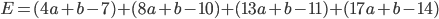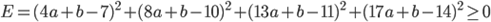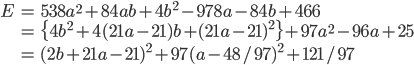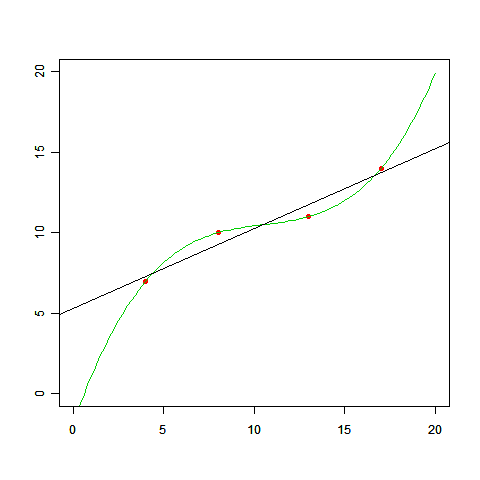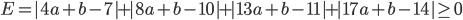「機械学習はじめよう」というタイトルの連載なのですが、実は今まで機械学習そのものの話がほとんどありませんでした……。今回からようやく機械学習がはじまります。
連載の第1回では、機械学習とは「解決したい問題」を数値化する「モデル」と、モデルのパラメータをデータから決める「学習」からなることを紹介しました。しかし、これだけ聞いて「なるほど、わかった」という人はまずいないでしょう。やはりもう少し具体的な説明が欲しいところですね。
そこで今回は、数ある機械学習の中でもっとも歴史のある手法を紹介します。他の新しい手法に比べてもずっとシンプルですが、そこにはちゃんと機械学習のエッセンスが詰まっています。そこから機械学習というものをより具体的に理解できるはずです。
2つの変数の関係を見つけよう
まずは例題として、2つの変数間の関係を調べてみましょう。「2つの変数」には、「気温と湿度」のようにいかにも関係ありそうな組み合わせだけではなく、「株価と犯罪発生率」のように関係があるかわからないような組み合わせもアリです(意味があるかどうかはまた別の話です)。
ここでは、どんな問題にも当てはめられるよう、2つの変数をxとyという2つの文字で表しましょう。そして、サンプルデータとして、以下の組み合わせを用意してみました。
(x,y)=(4,7),(8,10),(13,11),(17,14)
これらのデータをプロットすると、以下の図になります。
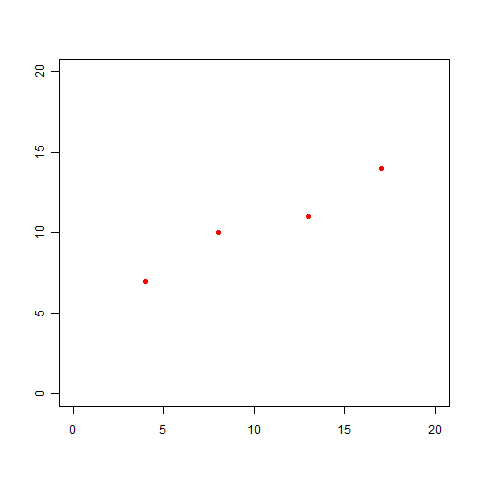
この図を見ると、次のような直線を引いてみたくなりますよね。
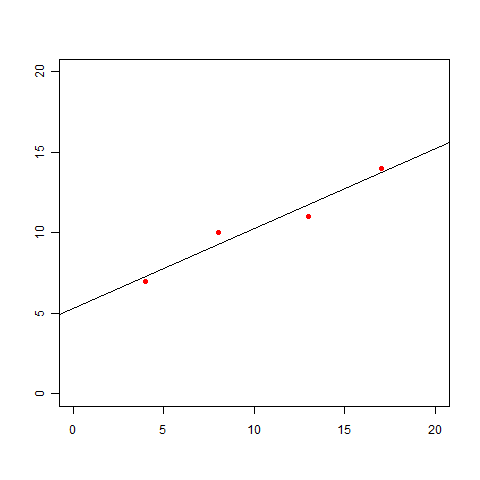
「ん〜、だいたいこんな感じ?」でいいのであれば、このグラフを見せれば事足りるかもしれません。しかし、この直線の式 y=ax+b が欲しいという話になった場合にはどうしましょう。「グラフから判断すると、bはきっと5くらいだな」では多分許してくれません。
最小二乗法
こういうときに使える有名な手法が「最小二乗法」です。聞いたことある、使ったことあるという人もきっと多いでしょう。まずは、復習を兼ねて「最小二乗法」を簡単に試してみましょう。
求めたい直線の式を y=ax+b とします。この直線はサンプルデータの最初の点 (x,y)=(4,7) の近くを通るはずです。つまり、x=4 のときの値 y=4a+b と y=7 との差 4a+b-7 はできるだけ小さくしたいです。同様にその次の点 (x,y)=(8,10) での差 8a+b-10 も小さくしたいですし、その次も、次も……。どれか1つなら簡単ですが、全体的に小さくしたい。それでは、差の合計が小さく(0に近く)なるようにしたらどうでしょう。
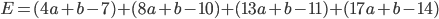
すぐわかりますが、これではダメです。なぜなら、それぞれの差が負の値になることもあるため、大きい正の値と大きい負の値がキャンセルしあってしまいます。そこで、それぞれの差の二乗をとってから足しあわせることにしましょう。これを「二乗誤差」と言います。
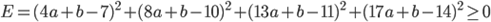
この値が小さくなるようにaとbを決めれば、すべての点での差をできるだけ小さくなるように決めた、と言えそうです。しかも嬉しいことに、この式はaとbの2次式なので、平方完成(懐かしいですね!!)を行うことで最小値を求めることができます。
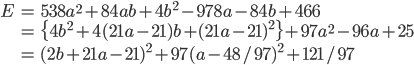
この式が最小となるのは 2b+21a-21=0, a-48/97=0 のときなので、a=48/97≒0.495, b=1029/194≒5.28 とわかり、したがって直線の式は y=0.495x+5.28 と求まりました。
きちんと値が求まって気持ちいいですね。でも、ここまでの短い話の中で大きな仮定がなんと3つもありましたが、気づきましたか?
隠されていた3つの仮定
1つめの仮定:関数の形
試しに別のサンプルデータを使ってちょっと考えてみましょう。
(x,y)=(0.0,4.0),(2.0,0.0),(3.9,3.0),(4.0,2.0)
このデータをプロットしてみます。
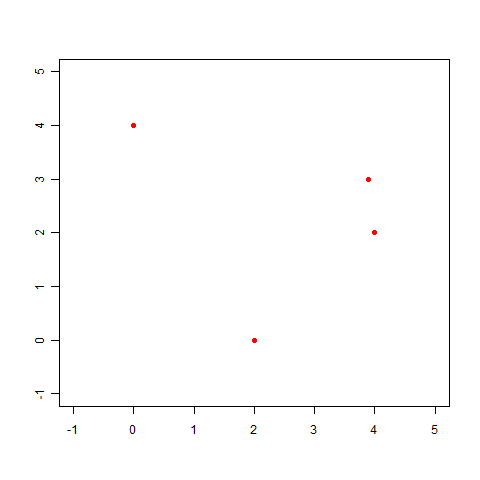
この点に近い直線も最小二乗法を使って求められますが、こんなグラフになってしまいます。これは明らかに変ですね。
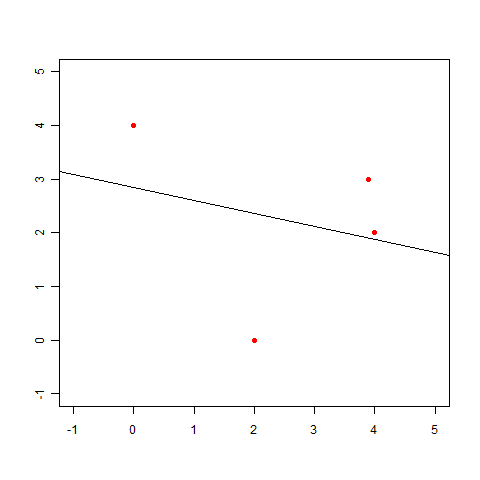
これはきっと直線じゃあなくてもうちょっと曲がった線を引かないと……って、あれ? ちょっと待ってください。
このグラフが変だってことは明らかなのだとしても、最初の例題で引いた線を直線にしなければいけないと、いつ決まったんでしょう? 最初の例題で曲線を引いていいのであれば、以下のようなグラフも描けるわけです(下図の緑の線)。
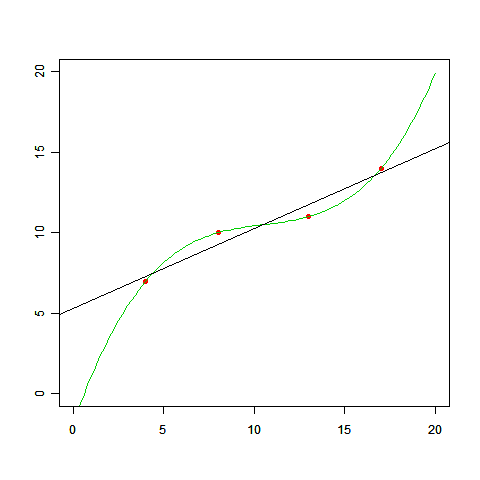
これならすべての点を通っていますから、正確さで言えばむしろ直線より良くなっています。一体どちらが「正解」なんでしょう。
これが授業であれば「直線が正解だと思う人~?」「いやいや曲線でしょ、って人~?」と手を挙げてもらうところですね(笑)。でも実は、今与えられている情報だけではどちらが良いかなんて言えません。もっとはっきり言うと、そもそも機械学習に「正解」なんてないのです。
「直線」と「曲線」のどちらが良いかは、「問題を解きたい人はどちらが欲しいか」なのです。そしてそれを決めるのは、“そのデータがどういう由来なのか”“結果をどのように使おうとしているのか”であるため、データだけを見てどちらが良いなんて言えないんですね。つまり、「モデルとして直線を考える」のは、データからは決して導くことのできない仮定だったのです。
2つめの仮定:二乗誤差という指標
仮定のその2は「二乗誤差」のところに隠れています。差の二乗を取ってプラスとマイナスが打ち消しあわないようにしましたが、以下のように、差の絶対値を取ることでも同じ効果が得られます。
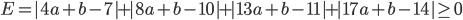
二乗誤差よりも多少面倒ですが、この式を最小にするaとbを求めることもできて、(a,b)=(7/13,63/13) であることがわかります(下図の緑の線)。
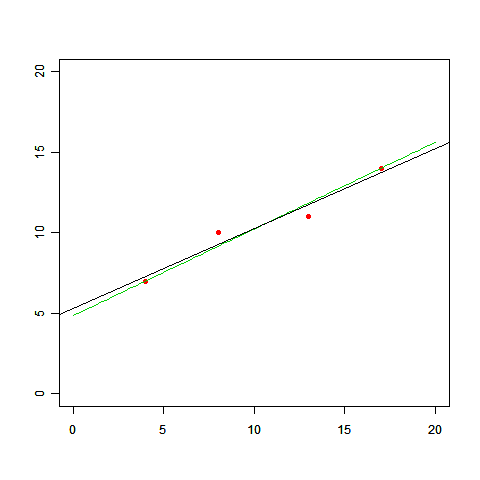
さきほどの「直線と曲線のどちらがいいか」でも悩ましい問題でしたが、今度は「どちらの直線を選ぶか」ですからね。データだけから決めるのはますます無理です。つまり、「適切なパラメータを選ぶ指標として二乗誤差を使う」こともデータから導くことのできない仮定だった、ということです。
実は、二乗誤差の最小化は、差の分散を最小化してくれることがわかっています。つまり、どの点にもできるだけ同じくらいの誤差がのっているような調整をするわけです。しかも計算しやすいというメリットもあるため、二乗誤差を使うというのは比較的必然性のある仮定ではあります。とはいえ、データに含まれる誤差が偏っていることがわかっている場合などはその限りではありませんので、いつでも必ず二乗誤差を使うというわけにはいかないということです。
3つめの仮定:「関数」という関係
さて、残る仮定はあと一つ。それをあぶり出すために「今までデータ点が4つしかありませんでしたが、さらに96個ものデータを取ってくることができた」という設定を考えてみましょう。データが多ければ多いほど、より正確で精密な直線の式を得ることがきっとできるでしょうから、もちろん大歓迎ですよね。
さて、追加されたデータも含めてグラフにプロットしてみました。
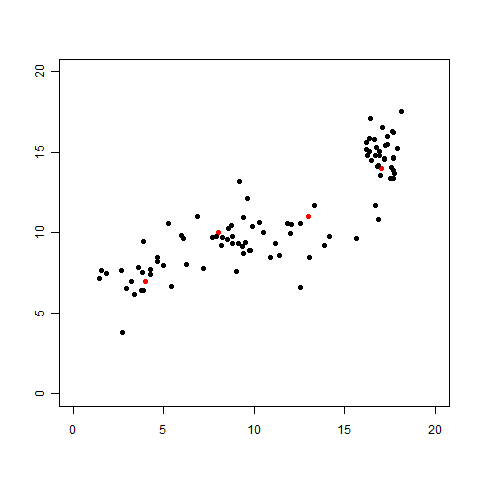
「あ、直線も曲線も引けない……。直線っぽく見えたのは最初の4個がたまたまそういう感じに見えていただけだったのか……」ということに気づくはずです。わざとらしい展開ですが、これでわかるとおおり、そもそもの一番最初の最初におこなおうとした「2つの変数間の関係を関数で表す(表せる)」というのも仮定だったのです。
まとめ、そして「回帰」へ
以上のように、データから最小二乗法で直線を推定する場合、実は仮定が3つ隠れていたことがわかりました。まとめてみましょう。
- 変数間の関係を関数で表す
- 関数のモデルは直線(1次式)を考える
- パラメータを選ぶ基準として二乗誤差を用いる
これらはどれも、与えられているデータだけからは妥当性を判断しきれない「仮定」だったわけです。どれもなかなか強い仮定ですが、これらを認めてさえしまえば、最小二乗法はその範囲で最適な答えを簡単に見つけてくれます。
機械学習のすべての技術は、このような仮定を大なり小なり必ず持っています。「どこまでが仮定なのか、その仮定は解きたい問題に対して適切か」という認識は、機械学習を効果的に使うために最も重要なポイントになりますので、常に意識するようにしておきましょう。
ちなみに、変数間の関係を関数で表すことを機械学習では「回帰」と言います。そして計算しやすさは最小二乗法のままで、2つめの仮定をもっと柔軟にできるようにしたのが「線形回帰」です。そこで、次回の後編ではこの「線形回帰」を紹介します。