概要
統計分析の基本を,プロ野球の分析を通して学ぶ入門書です。多くの方がイメージしやすく,かつ分析に必要なデータを取得しやすいプロ野球の分析を題材にすることで,統計分析の手法や結果の考察方法を,初学者の方にもわかりやすく解説します。どのようにグラフ化すると傾向がつかみやすいのか,一見関連がわからない数値同士の相関をどのように見つけ出すのかなど,統計分析の基礎から実践までを,実際に分析を行いながら学びます。
こんな方におすすめ
- 身近な野球のデータを利用してこれから統計学を学びたい方
サポート
ダウンロード
(2017年3月10日更新)
以下のサンプルコードファイルをダウンロードできます。圧縮ファイルをダウンロードしていただき,適宜解凍してご利用ください。
- ダウンロード
- サンプルコードファイル(statistics_guide_sampledata.zip)
正誤表
本書の以下の部分に誤りがありました。ここに訂正するとともに,ご迷惑をおかけしたことを深くお詫び申し上げます。
P.34 「四分位偏差」の見出しおよび1~3段落行目
| 誤 |
四分位偏差
データを大きい順番に並べ4分割したときの、上から25%と下から25%にあたる値を四分位偏差(Quartile Deviation:Q)と言います。ちょうど50%にあたる中央値とセットで示すことで、中央値±25%とデータ全体の半分の分布を示すことができます。
この分位というのは、データを分割した際の境目にあたる値のことを言います。四分位だとデータを4分割した境目なのでデータの小さいほうから25%、50%、75%の値が四分位となります。このうち25%の値を第1四分位(Q1)、50%の値を第2四分位(Q2=中央値)、75%の値を第3四分位(Q3)と呼びます。この分割数を10にした十分位数(decile)、分割数を100にした百分位数(パーセンタイル:percentile)というものもあります。
四分位偏差の関係を図で表したものが図2.9です。1から100までの数値を並べたときの25%、50%、75%の値を確認できるでしょうか。この図のように1から100までの数値であれば四分位偏差の位置を考えるまでもありませんが、実際に集めたデータを小さい順に並び替えて四分位偏差の値を探すのは大変ですので、Excelで計算するのがよいと思います。 |
|---|
| 正 |
四分位数
データを大きい順番に並べ4分割したときの、上から25%と下から25%にあたる値を四分位数(quartile points)と言います。ちょうど50%にあたる中央値とセットで示すことで、中央値±25%とデータ全体の半分の分布を示すことができます。
この分位というのは、データを分割した際の境目にあたる値のことを言います。四分位だとデータを4分割した境目なのでデータの小さいほうから25%、50%、75%の値が四分位となります。このうち25%の値を第1四分位(Q1)、50%の値を第2四分位(Q2=中央値)、75%の値を第3四分位(Q3)と呼びます。この分割数を10にした十分位数(decile)、分割数を100にした百分位数(パーセンタイル:percentile)というものもあります。
四分位数の関係を図で表したものが図2.9です。1から100までの数値を並べたときの25%、50%、75%の値を確認できるでしょうか。この図のように1から100までの数値であれば四分位数の位置を考えるまでもありませんが、実際に集めたデータを小さい順に並び替えて四分位数の値を探すのは大変ですので、Excelで計算するのがよいと思います。 |
|---|
P.34 図2.9
| 誤 |
四分位偏差の各指標の位置付け |
|---|
| 正 |
四分位数の各指標の位置付け |
|---|
P.35 上から3段落目
| 誤 |
この関数で四分位偏差だけではなく、最小値と中央値、最大値まで計算できるので便利な関数です。データの散らばりを表す値としては標準偏差のほうが使われることが多いのですが、25%という分割方法が直観的にわかりやすいというメリットが四分位偏差にはあります。 |
|---|
| 正 |
この関数で四分位数だけではなく、最小値と中央値、最大値まで計算できるので便利な関数です。データの散らばりを表す値としては標準偏差のほうが使われることが多いのですが、25%という分割方法が直観的にわかりやすいというメリットが四分位数にはあります。 |
|---|
P.70 「箱ひげ図 ── 複数の情報を一度に表現する」の1段落1行目
P.70 「打率の分布を比較する」の2段落3行目
| 誤 |
四分位偏差の値となります。 |
|---|
| 正 |
四分位数の値となります。 |
|---|
P.71 「箱ひげ図を作成する」の2段落2行目
P.106 本文中の図版
| 誤 |
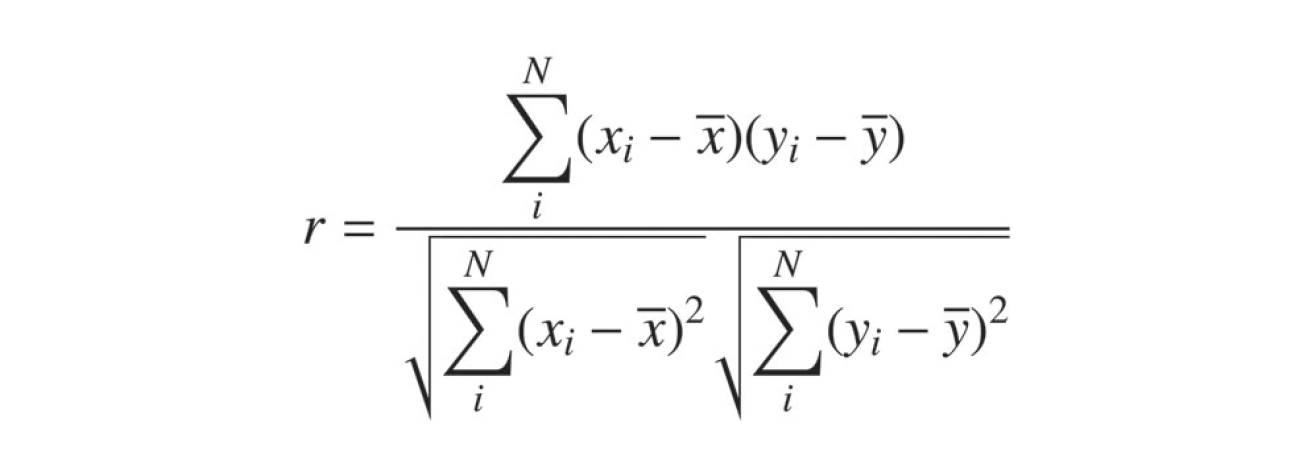
|
|---|
| 正 |
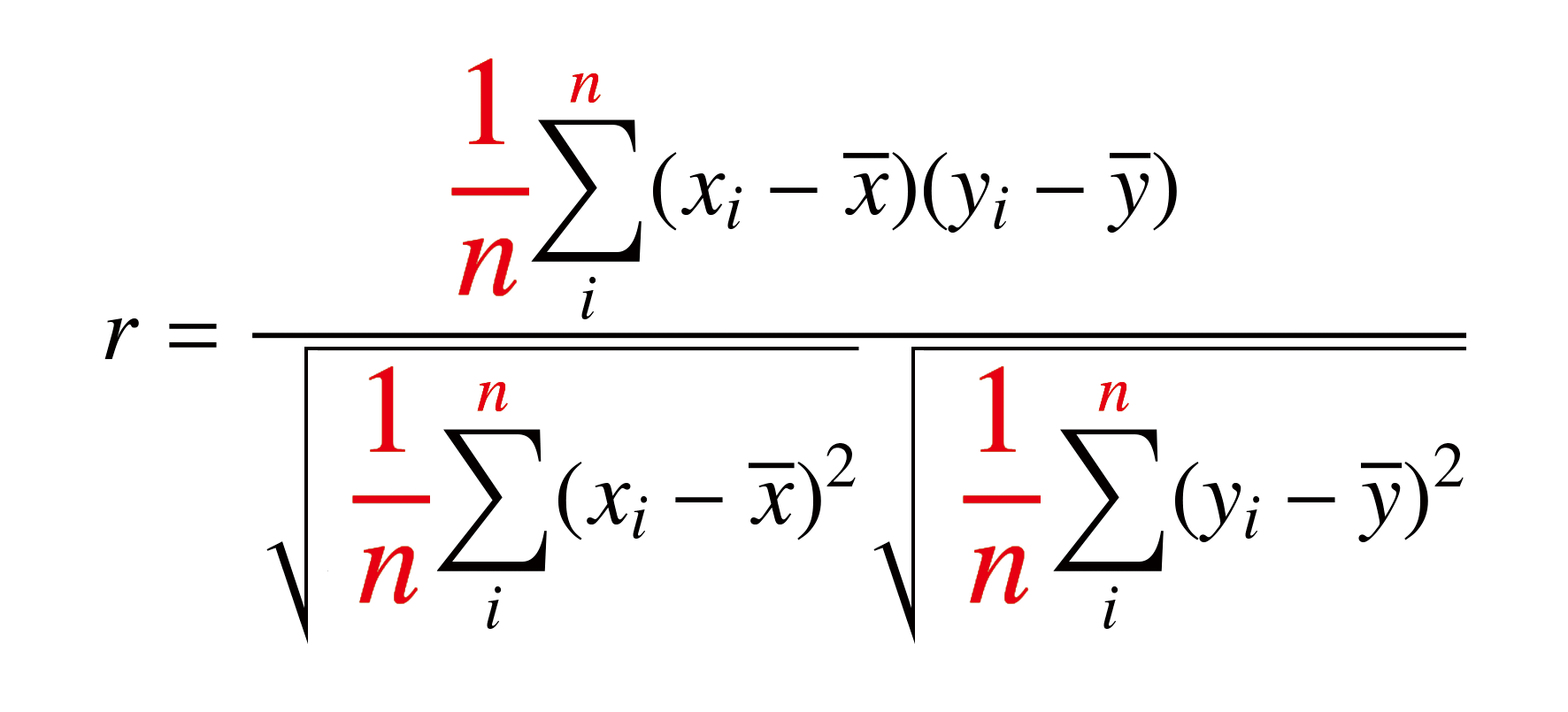
|
|---|