前回は、平行ケーブルや同軸ケーブルに伝播する電磁波の進行速度を調べるための実験を紹介しました。そして筆者が、学生時代に解析計算や実験をしていた不思議な波動のことに触れました。
今回はその波動を紹介しながら、波動の速度には位相速度と群速度の2つがあることを語りたいと思います。
発端
これは本書(『ピタゴラスの定理でわかる相対性理論』)のあとがきに次のように記したことに関連します。
『大学院に進学して理学部物理学科の講義を聴講したとき、ヨーロッパに展開された物理学の歴史が熾烈なものだったことを知った。相対性理論も聞いたが、プラズマ中の波動を調べるための実験装置を製作する傍らで到底理解できるような科目ではなく不満足感が残った。』
このように筆者は、プラズマに伝播する波動を観測するための実験装置の制作に情熱をかけながら相対性理論の講義を聴きに行ったのです。しかし、なかなかこの基本的な物理学の理解には至りませんでした。相対性理論はアインシュタインが光速不変を公理として作り上げた物理学です。本書はこの物理学の数学的背景を語ったものですが、これを書くための勉強の機会を得たときは還暦を過ぎていました。
波の2つの速度
私たちの周辺にはさまざまの種類の波動があります。いろいろな波動の中で、基本的なのが光や電磁波だろうと思います。基本的とは、形を変えずに伝播することです。
線路の場合には、発信源から双方向に波動が伝播します。真空中では観測者の速度に関係なく一定の速度cで伝播する波動が光や電磁波です。
地震も波動の一種で、縦波と横波があって進行速度が異なります。
海岸に押し寄せる大きな波は、岸に近づくときに形が急激に変化して、覆いかぶさるようにして岸に押し寄せます。
昔から打ち寄せる波という表現はあるのですが、逆に(津波が引くときを別として)海岸から遠ざかる波のことをあまり聞きません。この波は一方向に伝播する波動のようです。
図1を見てください。筆者が研究していた蛍光灯のようなガラス管に閉じ込められたプラズマ中の移動縞と呼ばれる波動です。この波動も、以下のように、打ち寄せる波のような不思議な性質をもっています。
- 一方向にしか伝播しない
- 遠方から発信源に向かって進行する
図1
日常的な体験では、山に向かってヤッホーと叫ぶとこだまが返ってくるのですが、ここでは、こだまだけが人に返って来るようにも考えられる波動です。
何かが根本的に違うはずです。それは、波動の進行という問題に関係します。
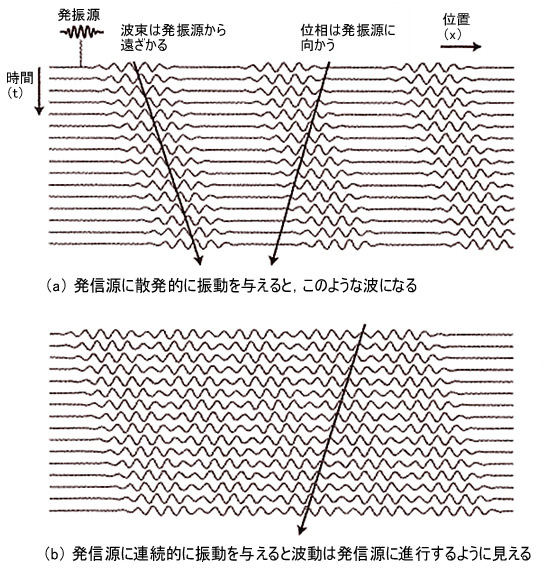
波動にはエネルギーが伴いますから、図2のように発信源から波動の塊(かたまり)(波束)を入れると、そこから一方向あるいは双方向にエネルギーが走っていくことは認めることにします。
図2
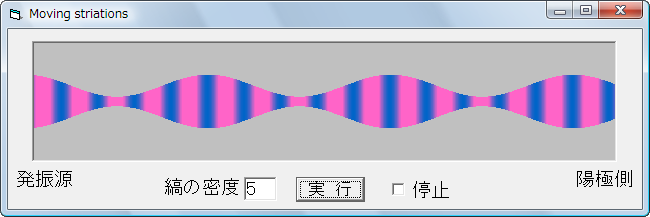
移動縞をシミュレーションさせるための、簡単なプログラムを作成しました。次のリンクからダウンロードできますので、実行してみてください。「実行」ボタンを押すだけで移動縞を確認できます[1]。
図3 移動縞シミュレーション用ソフト「Moving striations」
ところが、塊の中の波の位相の変化をみると、発信源に進行しているのです。そこで、パルスの頻度を上げていくと連続します。すると波束が見えなくなり、位相だけが浮きできて波動の進行が、遠方から発信源に向かっているように見えるのです。
実をいうと、波動には2つの速度があります。
- 位相の進行速度を位相速度と呼びます。
- 波束(塊、群)の速度を群速度と呼びます。
移動縞は、群速度と位相速度が反対向きだったのです。
位相速度と群速度、その数学的扱い方
ここからは、専門用語を使った数学としての記述です。サラリと数学的な手続きを読んでください。無理して理解しようとしないでください。
光や弦の波動方程式は次ような形をしていました。

ここで時間微分を-iωとします。空間微分をikとします。つまり形式的に、次の置き換えをすることを意味します。
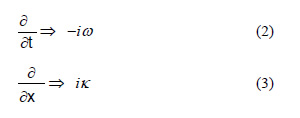
iは虚数単位、 ωは波動の角周波数、kは波動の波数(2πあたりの波の数)です。時間の2階微分それぞれ
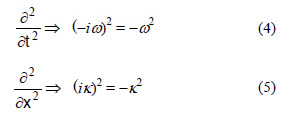
になります。
このような置き換えを波動方程式に代入して得られる代数式を、特性方程式と呼びます。
そして特性方程式から、ω/kを計算したものが位相速度で、微分dω/dkを計算したものが群速度です。
すると光や弦の波動方程式の場合は、次ようになります。

これより

となり,位相速度は

となるのです。ここで、プラスマイナスの符号が現われることが重要です。これはx軸にそって双方向に伝播する可能性を示すからです。
前回は、実際問題として一方の伝播を阻止するために、終端抵抗(terminator)というものを置くことを説明しました。
式(7)を>kで微分すると

となり、群速度と位相速度は同じです。
相対性理論では、何気なく光の速度とか光速と言っていたのは、本来は位相速度でしたが、同時に群速度でもありました。
ちなみに、電子は、波動と粒子の両方の性質をもつということがよく言われるのですが、その場合には、位相速度と群速度には違いがあります。それについては参考文献(1)に詳しく解説してありますので参考にしてください。
移動縞の波動方程式
では、次のような微分方程式で特徴づけら得る波動を調べてみましょう。

これに、式(2)(3)の関係を適用すると次式が得られます。

これより

を得て、両辺をkで微分すると
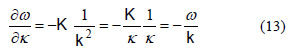
つまり

となります。
このように、群速度と位相速度は、大きさが同じで逆方向になります。
群は、波束とも呼ばれ、エネルギーを伝播します。ですから発信源から進行します。
一方、位相は、発信源へ逆伝播します。ということは、連続的に移動縞が発振されると、図1、2のように陽極から、陰極側に置いた発信源に向かって進行するように見えるということです。
空中の音波も、光と同じように、位相と群は同じ速度で移動します。光や音波などの波動と、移動縞は対照的な性質の波動だといえます。
(10)から(14)までの誘導を、指導教官の八田吉典教授からきいた時の印象は強烈でした。波動の不思議に感動したのです。教授から与えられた卒業研究の課題は、移動縞現象の解明でした。
移動縞がなぜこのような性質の波動になるのか? これはいまだに明快には解明されていないのではないかと思います。
プラズマというのは、気体分子が電磁界や熱のエネルギーによって、電離していている状態です。電離とは、気体分子がもっている電子の一部あるいは、全部が原子核の束縛を離れて自由に動きまわっている状態です。電子はマイナスの電荷をもち、分子はプラスの電荷をおびていますが、この状態がイオンです。実はイオンと電子は、ガラス管などの側壁で再結合します。
電子とイオンが混じった状態ですから、電磁界現象と気体の統計的現象と、さらに側壁での再結合があや織りなして複雑な波動が営まれているのが移動縞だろう、というのが教授からいただいたヒントでした。当時の東ドイツの研究所などで発表された論文では、式(14)に近い観測結果が得られていました。
この波動の方程式を導く計算に熱中しましたが、なかなか式(1)のような単純な理論式は、得られませんでした。理論の才能には恵まれていなかったのではないかと思います。修士課程に進んでからは、移動縞を観測する実験装置をつくることにしました。
ガラス管の太さと波長の関係
この波動現象が、ガラス壁での再結合に関係するものだとすると、ガラス管の太さにも関係するはずです。そこで、ごぼうのような形のガラス管を数個、研究室のガラス工の千葉さんという方に作ってもらって、陰極と陽極を取り付けて真空にしてからアルゴンを詰めて放電させて、波長を調べました。
すると、管径が大きい部分ほど、波長も長くなっていました。その実験結果のポイントを発表したところ、早速アメリカの海軍研究所やチェコスロバキアの研究所などから反響がありました。
移動縞は、肉眼ではただボーと光っているグローです。道具を使って初めて観測できる波動です。この実験をしたのは今から思うとかなり昔になるのですが、そこで使った装置は、今でも大変に重要な科学的意味をもっているのが不思議です。
まずガラスファイバーです。ガラスファイバーは、光を自由な経路で伝播する装置です。電波を伝達するための同軸ケーブルや平行フィーダ線と似ています。今ではインターネットなどの情報通信に欠かせない装置ですが、実用化され始めたときに早速これを使って、プラズマのグロー(glow)を光電子増倍管に引っ張ってきたのです。
光電子増倍管は、微弱な光の強弱を増幅する装置です。最高級品は日本製で、宇宙から飛来してくる素粒子の大掛かりな観測装置に多数使われています。もちろん前回写真で紹介したようなオシロスコープも自分の実験には使いました。
Internetで論文が見つかる
移動縞のことを英語でmoving striationsといいます。Googleでこの専門用語を検索すると、たくさんの研究論文が出てきます。
ためしに、自分の名前を加えてmoving striations kenjoとして絞込んでみたところ、もう45年も昔になってしまった学生時代に日本物理学会の欧文誌に寄稿した実験報告と、翌年就職してモータ研究に転向したときに書いた論文の抄録が出てきたのには感激しました。




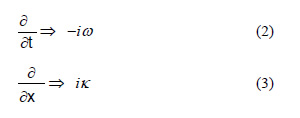
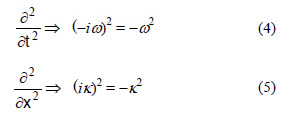
![]()
![]()
![]()


![]()
![]()