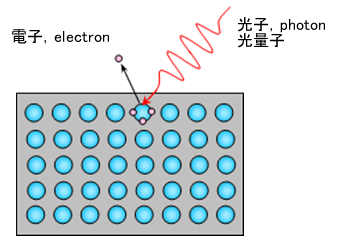
図2 のようなものかもしれません。
これは今日の電子工学の基礎の一つです。
図2 真空中におかれた金属に光を当てると、金属表面から電子が飛び出す。ただし、光は最小単位の粒(かたまり、量子)から構成され、1個の光量子(photon)のエネルギーはhν である。電子が金属表面の束縛を破って外に飛び出すための最小エネルギーW よりhν が大きいときには、電子が飛び出す。
時代の背景
少しだけ次代背景についてコメントします。プランクのこの発見の背景としてドイツの鉄鋼産業の国家事業がありました。1871年から20年間のビスマルク宰相の時代、ドイツは科学によって産業を興し、国家の研究所を建造する政策があったようです。
時の宰相ビスマルクは演説で次のように宣言しました。
Nicht durch Reden oder Majoritätsbeschlüsse werden die Großen Fragen der Zeit entschieden, sordern durch Eisen und Blut.
(見城・武口による英訳:Not through speeches or majority vote are the big problems of the time resolved but by iron and blood.)
意味:現在の大問題は演説や多数決ではなく、鉄と血でこそ解決されるのだ。
この演説は、鉄血演説として知られるようになったものです。ここで言う大問題とは、分裂状態のドイツ統一であり、鉄というのは優れた大砲のための良質な鉄のことです。溶鉱炉の中の状態を調べる技術が必要になると同時に、科学者の関心もここに集まったのです。
溶鉱炉の中は、コークスの炎で熱せられ低い周波数から高い周波数の輻射(放射、光)に満ちています。そういう状態の物理的な極限モデルとして、黒体というものがしきりに議論されるようになりました。電気回路の法則で有名なキルヒホッフ(1824-1887)は、この方面の草分けであり、彼のもとで学んだのがプランクです。
黒体輻射の温度と周波数と熱エネルギーの関係を物理学古典論で論じていくと、どうしても理論自体もおかしくなり、実験とも合わないことが明らかになってきました。そういう中でプランクは、「 光がとるエネルギーには有限最小値がある」とすると実験と合致することから、プランクの定数h を提唱しました。ウイーン大学ではボルツマンが、分子運動に関する統計力学を作り、マックスウェルの電磁気学を取り入れて熱力学を発展させていました。
20世紀明けのケルビン卿の講演
19世紀のイギリスでは蒸気機関が発明され、その科学技術が究められ、ケルビン卿らによって熱力学がかなり進歩していました。
そして20世紀に入り、1900年4月12日のイギリスの大御所ケルビン卿の講演、
「Nineteenth Century Clouds over the Dynamical Theory of Heat and Light」( 熱と光の力学を覆う二つの雲)
は今でも語り草になっています。
彼は19世紀のほとんど解き明かされて青空のような物理学について、
"beauty and clearness of theory" was overshadowed by "two clouds".
と語りました。
晴れ渡った空に2つの未解決の問題(雲)が残っているが、そのうちにすっかり晴れ渡ると考えたようです。その雲とは、
宇宙に充満しているエーテルに関する謎(エーテルの問題)
熱輻射のスペクトル分布の観測結果が理論と合わない(熱力学と光の関係)
の2つですが、この雲は大きくなり暗雲となってきました。
そして、コラム2に示したような当時有名になっていた役者のそろった舞台に、新鋭のアインシュタインが登場したのです。
1.の問題解決として、1905年に相対性理論を発表します。
2.については、光は連続量ではなく粒子であり、そのエネルーはhν であるとして解決されます。
しかし、このようにデビューはしたものの、既存の名優は彼の理論を納得しなかったというより、見えなかったのではないでしょうか? まさに事実は小説より奇なりの格言があてはまります。
コラム2:時代年表
1904年 時代が動く
モーリス・ド・ブロイ:ランジュバンのもとで物理を学び始める(弟のルイ・ド・ブロイに後年大きな影響をもたらす)
Lorentz(オランダ) :ローレンツ収縮の理論
ポアンカレ(Poincaré、仏) :セントルイス万国博覧会場のワシントン大学で相対性原理について講演
ハーゼンエール(Hasenöhrl、オーストリア):古典的電磁理論からE=(3/4)mc2 を導く
アインシュタイン(スイス) :オリンピアアカデミー、ベルンで討議を重ねる
アインシュタイン:Zur algemeinen molekularen Theorie der Wärme(熱の一般分子論)をAnnalen der Physikに寄稿, 光量子説の萌芽と思われることを発表。
長岡半太郎(日本) :土星のリング状の原子モデルを提唱
奇跡1905年
アインシュタイン:Annalen der Physikに決定的な論文を連続寄稿
1905年3月 光量子説;光は粒子であり、そのエネルギーはE=hν ではあるまいか;熱力学の考察から量子力学を開く
1905年5月 ブラウン運動
1905年 6月 特殊相対性理論;力学と電磁気学を統合
1905年 9月 相対性原理から、光の発生と質量に関するエネルギー則E=mc2 を導く
E=mc2 とE=hν の2つの式第10回 では、1905年9月のAnnalen論文で質量とエネルギーの関係を、実に見事な論法で導いてE=mc2 を得ていたことを取り上げました。
実はこの年の3月のAnnalen論文では、 E=hν を見事な論法で得ていたのです。これは光の最小単位があって、そのエネルギーがhν だというものです。ここでh はプランクの定数として知られる定数で、ν は周波数です。
ここではまず、この二つの簡単な式のつながりにメスを入れてアインシュタインがどんなことを考えたのか試論を提供します。
本稿のために、アインシュタインの1905年3月論文、
Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt(光の発生と変換に関する一発見的見解について)
の原文と、その日訳および英語訳を眺め、また湯川秀樹の「アインシュタイン選集」 の解説を数回読んでみたとき、かれこれ48年前のある教室の光景が思い出されたのに驚きました。
武内助教授の講義
筆者は、1958年に東北大学工学部に入って翌年の秋にできたばかりの電子工学科に進むことを決意しました。1年から2年前期の教養部での講義のなかで充実感を覚えたのが、物理学でした。当時の教養部の教授の中には、旧制第二高等学校の雰囲気をもつ先生が残っていました。新制高等学校の物理学では味わえない深みと幅のある講義を聴いて、中間試験と定期試験を3学期(1年半)もかけて受けていくもので、90点以上、ときには100点を取り続けたのが痛快でした。電子工学科を決めた理由の一つがここにありました。
そして2年生の後半だったか3年の前期だったか忘れたのですが、電子物性論に関する講義が、大阪大学理学部伏見康治研究室出身の新鋭の武内助教授により行われました。その講義には、通信工学科の先輩も聴講に来ていました。
この講義で聞いていたのが、まさにこのアインシュタイン選集の内容だったと思うのです。後ろの席の友人は「見城、この武内という助教授は優秀だな!」と耳元でささやき心の高ぶりを共有した思い出があります。そこに展開されるエントロピーの理論計算には、わかりやすく展開された教養部の物理とは違って、深さというか高さというより凄みを感じたものです。
コラム3:(独)heuristische (英)heuristic とは何か
3月論文のタイトルに使われているこの単語は、意味深長です。辞書では「発見的」となっています。発見を導くような考察という意味が汲み取れます。仮説的と記すほうが近いと思います。実際「アインシュタインの光量子仮説」などといいます。
アインシュタインの本当に画期的な仕事は光量子仮説だった
アインシュタインというと相対性理論ということですが、むしろ光電効果を論じた3月論文こそ画期的な論文と評価する人が多いのです。これは量子力学創出の論文とも言えるからです。
アインシュタインが光に関する疑問の解明に取り組んだのが19歳。そしていくつかの問題を解決したのが26歳です。筆者は20歳のときにそういう事柄について講義を受けていたのです。
残念ながら講義の細部までの納得には至らなかったし、疑問もいくつかありながら質問する勇気もなかったのは自分だけではなかったと思います。19-20世紀のヨーロッパで20年以上にもわたって議論されてきたことを、せいぜい1.5時間の講義を2回ほどで講義されるのですから無理もないことだったかもしれません。
その疑問の一つが、平衡状態にある黒体を論じるのに統計力学を一方で使い、他方では(ボルツマンが)マックスウェルの電磁気学で扱って結果を出しながら、空洞輻射の本質を解き明かされる部分で、不思議でもあり理解しがたい部分がありました。
今思うと質問するべきでした。というのは、そういう本質的な問題を学生に率直に指摘されたとき、教師は本当に理解したり疑問をもっていないと、自信のない答えになったり、言葉多くして要を得ない答弁のようなものになるからです。鋭い質問は、教師自身の自覚を促すものですから、学生は積極的に質問するのがよろしいと思います。
アインシュタインのこの時代には、すでに運動力学とか熱力学という風に、物理学の細分化というかジャンルが出来ていたのかもしれませんが、当人の頭の中では、そういうものすべてが、一体化、混沌化、統合化されて考察が進められていたのではあるまいかと思います。
アシンシュタインは重要結論を数式では表していなかった! 慎重さのためか?
アインシュタインは、共振という物理現象の特質を見抜き、エントロピー計算のテクニックを発揮して、光のエネルギーはhν の整数倍のはずだと論じます。9月論文でアインシュタインはE=mc2 という式を書いていません。これを文章で述べているのですから、今日流の卒論の指導教授からは注意を受けそうです。同じように3月論文でもE=hν とは明記してはいません。表1 を参照してください。
9月論文は手品のようでもあり、狐につままれたような感じがします。2つの座標系を設定して不変なものを定義しただけで、エネルギーと質量という宇宙存在の根源の特質が導かれるという内容だからです。ですから、この式の信頼性の検証には時間がかかったようです。数学的に正しいとした一人が、Rohrlichで1960年であることを第2回の補講に記しています。
表1 3月論文と9月論文のエネルギー式導出の対比
3月論文 9月論文 量子力学の光量子論 対性理論の帰結 式にすると E=hν E=mc2 原文では文章で記述 訳 低い密度の単色光輻射は、熱理論的関係において、あたかも大きさhν で互いに独立のエネルギー量子から成り立っているかのように振舞う。( 意訳)密度の低い単色光輻射は、互いに独立した大きさがhν のエネルギー量子から構成されているかのような熱理論特性を示す。 ある物体がエネルギーE を光の放射の形で放出すると、その質量がE /c2 だけ減る。
注: 原文では光速としてV を使っているがここではc とした。このように原文ではプランク定数h の代わりにその意味を示すRβ/N を使っている。
ただし
R :ガス定数β=h/k ( k.ボルツマン定数)N :モル数
別の側面から、もう一度考察してみましょう。1904年のコラムにも記したように、その年の7月のAnnalen der Physik(物理学年報)にハーゼンエール[2] は、輻射エネルギーの質量換算についてはE=(3/8)mc2 という式を導き、アブラハムの指摘によって計算ミスに気づいてE=(3/4)mc2 としました。このことについては第2回の補講に書いたとおりです。
ハーゼンエールの論文では、記号として今日と同じ光速のc やβ(=v/c) を使っていることにも注意したいと思います。
アインシュタインは1901年から毎年、この物理学年報には熱力学などの論文を発表していましたから、ハーゼンエールの仕事を知らなかったということは考えられません。
ですから、ハーゼンエールのような古典論による複雑な論理ではなく、6月の理論で輻射エネルギーと質量の関係を計算し直したら、係数が3/4ではなく1になってしまったとも解釈できると思います。
これは蛇足ですが、ハーゼンエールの論文では記号h が使われているのですが、空洞の容積のことです。まだプランク定数としてのh は確立していなかったようです。アインシュタインもh を使っていません。
それに、アインシュタインが数式としてはE=mc2 と記さなかったのは、表1に記した文章で計算の意味を慎重に表現しようとしたからかもしれません。
ハーゼンエールの式だけを見ると、質量の減少が大きなエネルギーを発生するという解釈も可能かもしれないのですが、彼は黒体が運動しているときには、輻射のエネルギーのために質量が若干増えたと解釈されることを論旨としているように考えられます。
[2] F. Hasenöhrl: Zur Theorie der Strahlung in bewegten Körpern, Annalen der Physik, 1904, pp.344-370