はじめに
前回 は、データ処理における並列性について説明しました。今回からは数回に渡って、当該データ処理における具体的な並列アルゴリズムについて説明します。まずはその準備として、並列システムの性能指標について見ていきます。
並列システムや並列アルゴリズムにおける性能指標
並列システムや並列アルゴリズムを評価する場合においては、スケーラビリティ(Scalability)という指標が用いられることがあります。スケーラビリティは、仕事量や計算資源などが増加したときの処理能力や性能特性を表すものであり、データ処理におけるスケーラビリティの指標は次の2つに分類することができます。
スピードアップ(Speed-up)
スケールアップ(Scale-up)
スピードアップは、あるジョブを処理する場合において、当該ジョブを処理する計算機などの計算資源を増やしたときに、当該ジョブの処理するための時間がどの程度低下するかを表す指標です(図1(a) ) 。一方、スケールアップは、計算資源を増やし、かつ、それに比例してジョブが処理すべき仕事量(データ量)を増やしたときに、当該ジョブの処理するための時間が同程度かを表す指標です(図1(b) )( ※1 ) 。
図1 スピードアップとスケールアップこれらの指標においては、どのようなケースでどちらを用いるかについては明確な基準はありません。著者の意見としては、アプリケーションに応じて適切に選択することが望ましいと考えています。たとえば、主記憶のサイズにより性能が大きく変わるようなアプリケーションにおいては、計算機などの計算資源のみを増やす場合、データ量に対する主記憶の総容量の割合は大きくなるため、スピードアップは必ずしも適切な指標ではない可能性があります。すなわち、当該ケースにおいては、スケールアップを用いるほうが適切であると考えられます。
スピードアップにおいては、N倍の計算資源を用いたときにジョブの実行時間が1/Nになる場合(Speedup=Nとなる場合)を、スピードアップが線形(リニアスピードアップ)であると言います。スケールアップにおいても同様に、現状のN倍の計算資源とN倍の仕事量を用いたときにジョブの実行時間が同一の場合(Scaleup=1)を、スケールアップが線形(リニアスケールアップ)であると言います。
データ処理の並列アルゴリズムやデータ処理システムは、理想的には線形なスケーラビリティを有することが望ましいですが[2] 、実際には当該特性を実現することは難しいと考えられています。たとえば、データを複数の計算機に均等に分割することは必ずしも容易ではないため、各計算機が同じ処理能力を持ち、独立に動作できる場合であっても、各計算機が当該分割データを処理する時間には差が生じ得ます。すなわち、N台の計算機を用いても、各計算機における仕事量は均等に1/Nにならず、ある計算機においては、仕事量×1/N よりも大きな仕事をする場合があります。さらに、並列データ処理においては、多くの場合、各計算機は独立して動作することはできず、何らかのインタラクションを相互に行います。すなわち、ある計算機の処理の完了を待って初めて次の計算機の処理が始められる、というような状況が少なからず起こるため、必ずしも常にすべての計算機がフルに稼働できるわけではありません。
並列データ処理系においては、これまで、高いスケーラビリティを有する並列アルゴリズムに関する研究が多く行われてきました。以降では、それらのうち基本的なものを紹介していきます。まずはその準備として、データ処理における基本的なアルゴリズムをかんたんに述べ、当該アルゴリズムの並列化版を紹介します。
[1] 計算機の数を増やしてシステムの処理能力を上げることをスケールアウト(scale horizontally)と言い、単一マシンにおいてプロセッサなどの計算資源を増やすことをスケールアップ(scale vertically)と言うことがありますが、これらと混同しないようにご注意ください。これらのスケーラビリティの指標として、上記2つが存在します。
データ処理のアルゴリズム
データ処理において用いられる主要なオペレータとしては、選択処理オペレータや結合処理オペレータなどがあり、当該オペレータの実現にはいくつかの基本的なアルゴリズムが用いられています。
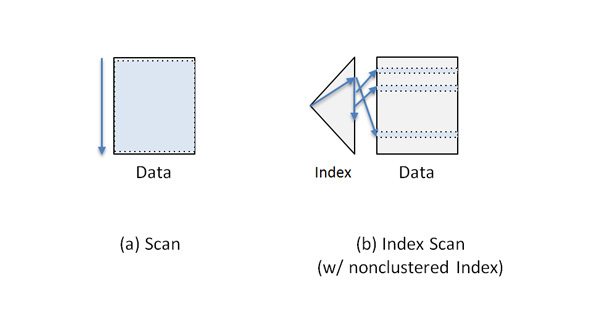
選択処理は、ある単一データ(または表)に対して、選択条件に合致したレコード(またはタプル)を取得する処理です。当該処理においては、データを先頭から末尾まで走査していく方法(スキャン)や、データに対する索引を用いて、選択条件に合致した索引エントリに対応するレコードのみを取り出す方法(索引スキャン)などがあります。
一方、結合処理は、複数のデータを、当該データを構成するレコードにおける属性値を用いて(たとえば、同一であるなどの特定の条件に基づいて)連結することにより、1つのデータにする処理です。当該処理においては、おもにソートマージ結合、ハッシュ結合、ネステッドループ結合の3つの方法が考案されてきました。
まとめると、選択処理と結合処理においては、一般的にはそれぞれ次のようなアルゴリズムが存在します。
選択処理(Selection)
スキャン(Scan)
索引スキャン(Index Scan)
結合処理(Join)
ソートマージ結合(Sort-Merge Join)
ハッシュ結合(Hash Join)
ネステッドループ結合(Nested Loop Join)
以降においては、当該アルゴリズムを並列化したもの(並列アルゴリズム)について説明します。
選択処理における並列アルゴリズム
選択処理を実現するには、大きく分けて、スキャンと索引スキャンの2つの方法があることを説明しました。スキャンは、前述のとおり、データを先頭から末尾まで走査するという方法です(図2(a) ) 。一方、索引スキャンは、選択条件に指定された属性に対する索引(非クラスタ化索引[3] を想定)がある場合は、選択条件に合致した索引エントリに対応するレコードを読み出すという方法です(図2(b) ) 。
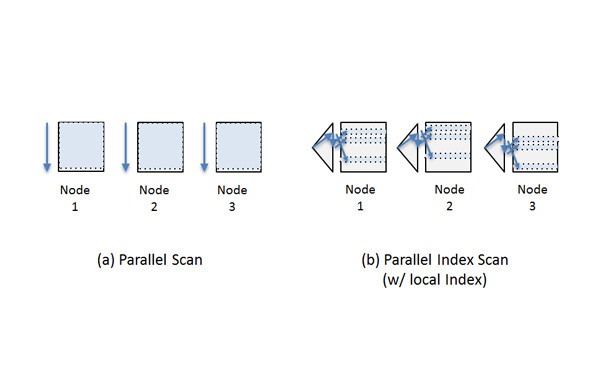
図2 選択処理のアルゴリズム選択処理は単一のデータを読み出すだけなので、その並列化においては、基本的には、当該処理を各計算機で並列に行うことができます。すなわち、並列スキャンにおいては、各計算機が当該計算機内の分割データを、ほかの計算機の読み出しとは関係なく(すなわち独立に) 、読み出します(図3(a) ) 。また、並列索引スキャンにおいても、分割データに対してそれぞれ索引が管理されている場合(すなわち、データの分割キーと索引の分割キーが同一であるローカル索引[3] は、並列スキャンと同様に、各計算機が当該計算機内の索引と分割データを、ほかの計算機の読み出しとは関係なく読み出します。
図3 選択処理の並列アルゴリズム一方、データの分割キーと索引の分割キーが異なる場合(グローバル索引[3] は、各計算機がほかの計算機内の分割データを読み出すことがあります。ただし、選択処理においては、索引エントリからデータへの参照にネットワークを介することがあるため、グローバル索引を用いることは少ないと考えられます。グローバル索引は、後の回で紹介するネステッドループ結合などで用いられることがあります。
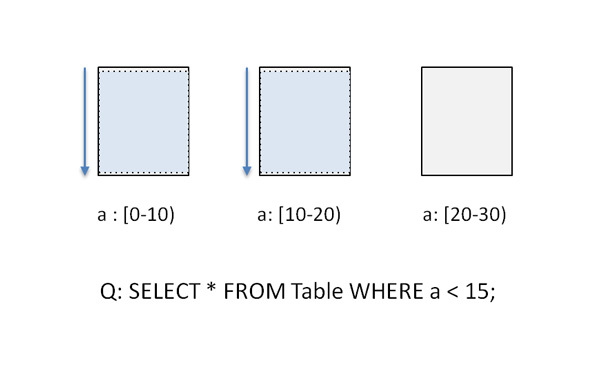
また、データの分割方法と選択条件によっては、アクセスすべき計算機を限定できる場合があります(図4 ) 。たとえば、データが範囲分割により複数の計算機に分散していて、データの分割キーと選択条件において指定された属性が一致する場合は、選択条件に該当する計算機のみにアクセスします。
図4 データ分割を利用してアクセスする計算機を絞り込む場合[3] 非クラスタ化索引とは、索引におけるキーの順番が、当該キーが参照するレコードの順番と異なるような索引構造です。非クラスタ化索引は、二次索引とも呼ばれます。クラスタ化索引とは、索引におけるキーの順番が、当該キーが参照するレコードの順番と同一であるような索引構造です。
Hadoopなどにおける選択処理
HadoopのMap処理においては、上記で述べたような並列スキャンを行います。すなわち、各Mapperは、HDFSを介してラウンドロビンで分割されたデータ(ブロック)を都度選びだし、ほかのMapperの動作とは関係なく、当該ブロックを読み出します[4] 。Impalaの選択処理やSparkのmap()、filter()などの処理おいても、基本的な方法は同様です。
おわりに
今回は、並列システムの性能指標について紹介し、また、データ処理におけるアルゴリズムと、選択処理の並列化方法を紹介しました。次回以降は、結合処理の並列化方法について説明する予定です。