第11回から前回の第16回までで、

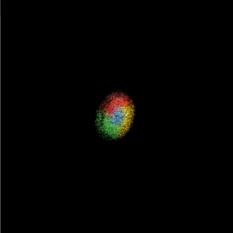
ロゴがひとつパーティクルで弾けるアニメーション
前のお題でわかったように、
見てのとおり、

var LoaderEvent = require("awayjs-core/lib/events/LoaderEvent");
var ColorTransform = require("awayjs-core/lib/geom/ColorTransform");
var Vector3D = require("awayjs-core/lib/geom/Vector3D");
var AssetLibrary = require("awayjs-core/lib/library/AssetLibrary");
var URLRequest = require("awayjs-core/lib/net/URLRequest");
var RequestAnimationFrame = require("awayjs-core/lib/utils/RequestAnimationFrame");
var View = require("awayjs-display/lib/containers/View");
var HoverController = require("awayjs-display/lib/controllers/HoverController");
var Mesh = require("awayjs-display/lib/entities/Mesh");
var PointLight = require("awayjs-display/lib/entities/PointLight");
var StaticLightPicker = require("awayjs-display/lib/materials/lightpickers/StaticLightPicker");
var PrimitivePlanePrefab = require("awayjs-display/lib/prefabs/PrimitivePlanePrefab");
var Cast = require("awayjs-display/lib/utils/Cast");
var ParticleAnimationSet = require("awayjs-renderergl/lib/animators/ParticleAnimationSet");
var ParticleAnimator = require("awayjs-renderergl/lib/animators/ParticleAnimator");
var ParticlePropertiesMode = require("awayjs-renderergl/lib/animators/data/ParticlePropertiesMode");
var ParticleBillboardNode = require("awayjs-renderergl/lib/animators/nodes/ParticleBillboardNode");
var ParticleBezierCurveNode = require("awayjs-renderergl/lib/animators/nodes/ParticleBezierCurveNode");
var ParticleInitialColorNode = require("awayjs-renderergl/lib/animators/nodes/ParticleInitialColorNode");
var ParticlePositionNode = require("awayjs-renderergl/lib/animators/nodes/ParticlePositionNode");
var DefaultRenderer = require("awayjs-renderergl/lib/DefaultRenderer");
var ParticleGeometryHelper = require("awayjs-renderergl/lib/utils/ParticleGeometryHelper");
var MethodMaterial = require("awayjs-methodmaterials/lib/MethodMaterial");
var MethodRendererPool = require("awayjs-methodmaterials/lib/pool/MethodRendererPool");
var PARTICLE_SIZE = 2;
var view;
var cameraController;
var light;
var assetsURL = "assets/chrome.png";
var bitmapData;
var colorValues = [];
var colorPoints = [];
var colorMaterial;
var colorAnimationSet;
var colorAnimator;
var timer;
var time = 0;
function initialize() {
var lightPicker = createLights();
view = createView(window.innerWidth, window.innerHeight, 0x0);
cameraController = setupCameraController(view.camera, 1000, 225, 10);
colorMaterial = createMaterial(lightPicker, true);
setListeners();
}
function createView(width, height, backgroundColor) {
var defaultRenderer = new DefaultRenderer(MethodRendererPool);
var view = new View(defaultRenderer);
view.width = width;
view.height = height;
view.backgroundColor = backgroundColor;
return view;
}
function setupCameraController(camera, distance, panAngle, tiltAngle) {
var cameraController = new HoverController(camera);
cameraController.distance = distance;
cameraController.panAngle = panAngle;
cameraController.tiltAngle = tiltAngle;
return cameraController;
}
function createLights() {
light = createPointLight(0xFFFFFF, 1, 600, 100, 2);
return new StaticLightPicker([light]);
}
function createPointLight(color, ambient, fallOff, radius, specular) {
var light = new PointLight();
light.color = color;
light.ambient = ambient;
light.fallOff = fallOff;
light.radius = radius;
light.specular = specular;
return light;
}
function createMaterial(lightPicker, bothSides) {
var material = new MethodMaterial();
material.bothSides = bothSides;
material.lightPicker = lightPicker;
return material;
}
function onResourceComplete(eventObject) {
var asset = eventObject.assets[0];
bitmapData = Cast.bitmapData(asset);
var colorGeometry = createParticles();
startParticleAnimation(colorGeometry);
}
function createParticles() {
colorAnimationSet = createColorAnimationSet(initColorParticle);
setParticlesData(bitmapData, PARTICLE_SIZE, colorValues, colorPoints);
var primitive = new PrimitivePlanePrefab(PARTICLE_SIZE, PARTICLE_SIZE, 1, 1, false);
var geometry = primitive.geometry;
var colorGeometrySet = [];
var count = colorPoints.length;
for (var j = 0; j < count; j++) {
colorGeometrySet[j] = geometry;
}
var colorGeometry = ParticleGeometryHelper.generateGeometry(colorGeometrySet);
return colorGeometry;
}
function setParticlesData(bitmapData, size, colorValues, colorPoints) {
var bitmapWidth = bitmapData.width;
var bitmapHeight = bitmapData.height;
for (var i = 0; i < bitmapWidth; i++) {
for (var j = 0; j < bitmapHeight; j++) {
var point = new Vector3D(size * (i - bitmapWidth / 2), size * ( -j + bitmapHeight / 2));
var color = bitmapData.getPixel32(i, j);
var rgbColor = getRgbComponents(color);
rgbColor.scaleBy(1 / 255);
colorValues.push(rgbColor);
colorPoints.push(point);
}
}
}
function getRgbComponents(rgbColor) {
var rgbVector = new Vector3D();
rgbVector.x = (rgbColor & 0xff0000) >> 16;
rgbVector.y = (rgbColor & 0xff00) >> 8;
rgbVector.z = rgbColor & 0xff;
return rgbVector;
}
function createColorAnimationSet(initParticleFunc) {
var LOCAL_STATIC = ParticlePropertiesMode.LOCAL_STATIC;
var colorAnimationSet = new ParticleAnimationSet();
colorAnimationSet.addAnimation(new ParticleBillboardNode());
colorAnimationSet.addAnimation(new ParticleBezierCurveNode(LOCAL_STATIC));
colorAnimationSet.addAnimation(new ParticlePositionNode(LOCAL_STATIC));
colorAnimationSet.addAnimation(new ParticleInitialColorNode(LOCAL_STATIC, true, false, new ColorTransform(0, 1, 0, 1)));
colorAnimationSet.initParticleFunc = initParticleFunc;
return colorAnimationSet;
}
function startParticleAnimation(colorGeometry) {
var scene = view.scene;
var colorParticleMesh = new Mesh(colorGeometry, colorMaterial);
var animator = new ParticleAnimator(colorAnimationSet);
colorAnimator = animator;
colorParticleMesh.animator = animator;
scene.addChild(colorParticleMesh);
}
function setListeners() {
timer = new RequestAnimationFrame(render);
timer.start();
AssetLibrary.addEventListener(LoaderEvent.RESOURCE_COMPLETE, onResourceComplete);
AssetLibrary.load(new URLRequest(assetsURL));
}
function initColorParticle(properties) {
var BEZIER_END_VECTOR3D = ParticleBezierCurveNode.BEZIER_END_VECTOR3D;
var index = properties.index;
var endPoint = new Vector3D();
var rgb = colorValues[index];
properties.startTime = 0;
properties.duration = 1;
properties[BEZIER_END_VECTOR3D] = endPoint;
properties[ParticleInitialColorNode.COLOR_INITIAL_COLORTRANSFORM] = new ColorTransform(rgb.x, rgb.y, rgb.z, 1);
properties[ParticleBezierCurveNode.BEZIER_CONTROL_VECTOR3D] = getRandomVector3D(100);
properties[ParticlePositionNode.POSITION_VECTOR3D] = colorPoints[index];
}
function getRandomVector3D(radius) {
var angle0 = Math.random() * Math.PI * 2;
var angle1 = Math.random() * Math.PI * 2;
var x = radius * Math.cos(angle0) * Math.cos(angle1);
var y = radius * Math.cos(angle0) * Math.sin(angle1);
var z = radius * Math.sin(angle0);
return new Vector3D(x, y, z);
}
function render(deltaTime) {
time += deltaTime;
if (colorAnimator) {
var _time = 1000 * (Math.sin(time / 5000) + 1);
colorAnimator.update(_time);
}
view.render();
}初期設定で呼び出す関数
前掲コード1の初期設定の関数
- createLights()
- createView()
- setupCameraController()
- createMaterial()
- setListeners()
関数createLights()は、
var light;
function initialize() {
var lightPicker = createLights();
}
function createLights() {
light = createPointLight(0xFFFFFF, 1, 600, 100, 2);
return new StaticLightPicker([light]);
}
function createPointLight(color, ambient, fallOff, radius, specular) {
var light = new PointLight();
light.color = color;
light.ambient = ambient;
light.fallOff = fallOff;
light.radius = radius;
light.specular = specular;
return light;
}| LightBaseクラスのプロパティ | 値と機能 |
|---|---|
| ambient | 環境光の強さを示す0以上1以下の数値 |
| ambientColor | 環境光のカラー値を示す0から0xFFFFFFまでの整数 |
| color | 光のカラー値 |
| diffuse | 光の拡散する強さを示す0以上の数値 |
| fallOff | 光が届く距離の最大値 |
| radius | 光が届く距離の最小値 |
| specular | 光の反射する強さを示す0以上の数値 |
関数createMaterial()は、
var colorMaterial;
function initialize() {
colorMaterial = createMaterial(lightPicker, true);
}
function createMaterial(lightPicker, bothSides) {
var material = new MethodMaterial();
material.bothSides = bothSides;
material.lightPicker = lightPicker;
return material;
}関数setListeners()の仕事のひとつは、
var assetsURL = "assets/chrome.png";
var bitmapData;
function initialize() {
setListeners();
}
function setListeners() {
AssetLibrary.addEventListener(LoaderEvent.RESOURCE_COMPLETE, onResourceComplete);
AssetLibrary.load(new URLRequest(assetsURL));
}
function onResourceComplete(eventObject) {
var asset = eventObject.assets[0];
bitmapData = Cast.bitmapData(asset);
var colorGeometry = createParticles();
startParticleAnimation(colorGeometry);
}素材を読み込み終えたときのリスナー関数
- createParticles()
- startParticleAnimation()
パーティクルとアニメーションを定める関数
関数createParticles()は、
- createColorAnimationSet()
- setParticlesData()
パーティクルの幾何学情報のGeometryオブジェクト
var PARTICLE_SIZE = 2;
var colorValues = [];
var colorPoints = [];
var colorAnimationSet;
function createParticles() {
colorAnimationSet = createColorAnimationSet(initColorParticle);
setParticlesData(bitmapData, PARTICLE_SIZE, colorValues, colorPoints);
var primitive = new PrimitivePlanePrefab(PARTICLE_SIZE, PARTICLE_SIZE, 1, 1, false);
var geometry = primitive.geometry;
var colorGeometrySet = [];
var count = colorPoints.length;
for (var j = 0; j < count; j++) {
colorGeometrySet[j] = geometry;
}
var colorGeometry = ParticleGeometryHelper.generateGeometry(colorGeometrySet);
return colorGeometry;
}関数createColorAnimationSet()は、
function createColorAnimationSet(initParticleFunc) {
var LOCAL_STATIC = ParticlePropertiesMode.LOCAL_STATIC;
var colorAnimationSet = new ParticleAnimationSet();
colorAnimationSet.addAnimation(new ParticleBillboardNode());
colorAnimationSet.addAnimation(new ParticleBezierCurveNode(LOCAL_STATIC));
colorAnimationSet.addAnimation(new ParticlePositionNode(LOCAL_STATIC));
colorAnimationSet.addAnimation(new ParticleInitialColorNode(LOCAL_STATIC, true, false, new ColorTransform(0, 1, 0, 1)));
colorAnimationSet.initParticleFunc = initParticleFunc;
return colorAnimationSet;
}| ParticleNodeBaseのサブクラスのコンストラクタ | 機能 |
|---|---|
| ParticleBezierCurveNode(モード, コントロールポイント, 終点) | 時間に応じた位置をベジエ曲線で定める |
| ParticleBillboardNode() | パーティクルの角度をつねにカメラに向ける。 |
| ParticleColorNode(モード, 乗数データの使用, オフセットデータの使用, usesCycleの使用, usesPhaseの使用, 初めの色, 終わりの色) | パーティクルアニメーションの時間に応じた色の変わり方を定める |
| ParticleInitialColorNode(モード, 乗数データの使用, オフセットデータの使用, 初めの色) | パーティクルの初めの色を定める |
| ParticlePositionNode(モード, 位置ベクトル) | パーティクルの初めの位置を定める |
| ParticleScaleNode(モード, usesCycleの使用, usesPhaseの使用, 最小伸縮率, 最大伸縮率) | パーティクルアニメーションが時間に応じてどう伸縮するかを定める |
| ParticleVelocityNode(モード, 速度ベクトル) | パーティクルアニメーションが始まるときの速度を定める |
関数setParticlesData()には、
setParticlesData(BitmapDataオブジェクト, パーティクルの大きさ, カラー値の配列, 位置の配列)BitmapDataオブジェクトのピクセルごとのカラー値
関数getRgbComponents()は、
function setParticlesData(bitmapData, size, colorValues, colorPoints) {
var bitmapWidth = bitmapData.width;
var bitmapHeight = bitmapData.height;
for (var i = 0; i < bitmapWidth; i++) {
for (var j = 0; j < bitmapHeight; j++) {
var point = new Vector3D(size * (i - bitmapWidth / 2), size * ( -j + bitmapHeight / 2));
var color = bitmapData.getPixel32(i, j);
var rgbColor = getRgbComponents(color);
rgbColor.scaleBy(1 / 255);
colorValues.push(rgbColor);
colorPoints.push(point);
}
}
}
function getRgbComponents(rgbColor) {
var rgbVector = new Vector3D();
rgbVector.x = (rgbColor & 0xff0000) >> 16;
rgbVector.y = (rgbColor & 0xff00) >> 8;
rgbVector.z = rgbColor & 0xff;
return rgbVector;
}関数startParticleAnimation()は、
function startParticleAnimation(colorGeometry) {
var scene = view.scene;
var colorParticleMesh = new Mesh(colorGeometry, colorMaterial);
var animator = new ParticleAnimator(colorAnimationSet);
colorAnimator = animator;
colorParticleMesh.animator = animator;
scene.addChild(colorParticleMesh);
}パーティクルを初期化する関数
パーティクルを初期化する関数は、
プロパティParticleProperties.
今回のアニメーションの動きを決める鍵となるのは、
すると、
function initColorParticle(properties) {
var BEZIER_END_VECTOR3D = ParticleBezierCurveNode.BEZIER_END_VECTOR3D;
var index = properties.index;
var endPoint = new Vector3D();
var rgb = colorValues[index];
properties.startTime = 0;
properties.duration = 1;
properties[BEZIER_END_VECTOR3D] = endPoint;
properties[ParticleInitialColorNode.COLOR_INITIAL_COLORTRANSFORM] = new ColorTransform(rgb.x, rgb.y, rgb.z, 1);
properties[ParticleBezierCurveNode.BEZIER_CONTROL_VECTOR3D] = getRandomVector3D(100);
properties[ParticlePositionNode.POSITION_VECTOR3D] = colorPoints[index];
}
function getRandomVector3D(radius) {
var angle0 = Math.random() * Math.PI * 2;
var angle1 = Math.random() * Math.PI * 2;
var x = radius * Math.cos(angle0) * Math.cos(angle1);
var y = radius * Math.cos(angle0) * Math.sin(angle1);
var z = radius * Math.sin(angle0);
return new Vector3D(x, y, z);
}パーティクルをアニメーションさせる関数
関数setListeners()は、
RequestAnimationFrame()コンストラクタに渡したコールバック関数
var time = 0;
function setListeners() {
timer = new RequestAnimationFrame(render);
timer.start();
}
function render(deltaTime) {
time += deltaTime;
if (colorAnimator) {
var _time = 1000 * (Math.sin(time / 5000) + 1);
colorAnimator.update(_time);
}
view.render();
}試しに、
function render(deltaTime) {
time += deltaTime;
// var _time = 1000 * (Math.sin(time / 5000) + 1);
// colorAnimator.update(_time);
colorAnimator.update(time / 5);
}三角関数のsinは、
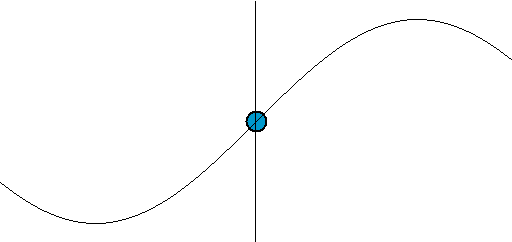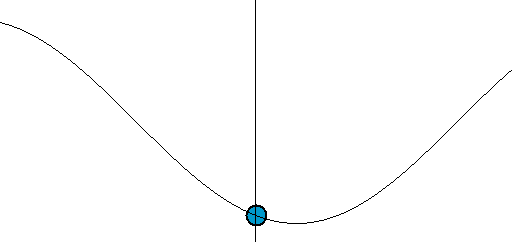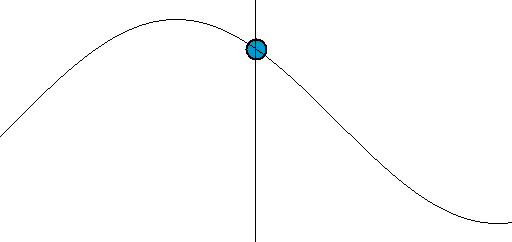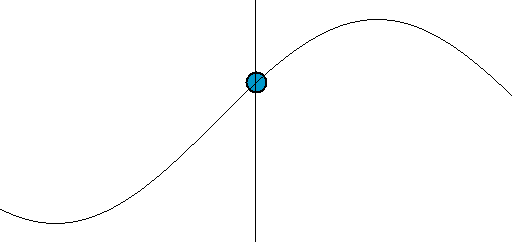
ようやく、
次回からは、



