前回は、


オブジェクトが引合う力の範囲をかぎる
互いに離れれば離れるほど、
もともと、
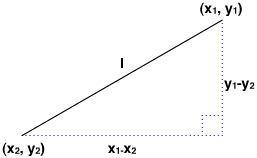
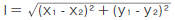
そこで、
水平・
function spring(object0, object1) {
var distanceX = object1.x - object0.x;
var distanceY = object1.y - object0.y;
var squareX = distanceX * distanceX;
var squareY = distanceY * distanceY;
var distance = Math.sqrt(squareX + squareY);
if (distance < limit) {
var accelX = distanceX * ratio;
var accelY = distanceY * ratio;
object0.velocityX += accelX;
object0.velocityY += accelY;
object1.velocityX -= accelX;
object1.velocityY -= accelY;
}
}さて、
// var limit = 100;
var limit = 100 * 100;
function spring(object0, object1) {
var distanceX = object1.x - object0.x;
var distanceY = object1.y - object0.y;
var squareX = distanceX * distanceX;
var squareY = distanceY * distanceY;
// var distance = Math.sqrt(squareX + squareY);
// if (distance < limit) {
if (squareX + squareY < limit) {
var accelX = distanceX * ratio;
var accelY = distanceY * ratio;
object0.velocityX += accelX;
object0.velocityY += accelY;
object1.velocityX -= accelX;
object1.velocityY -= accelY;
}
}書き直したJavaScript全体は、

var stage;
var stageWidth;
var stageHeight;
var balls = [];
var ballCount = 25;
var ratio = 1 / 2000;
var limit = 100 * 100;
function initialize() {
var canvasElement = document.getElementById("myCanvas");
stage = new createjs.Stage(canvasElement);
stageWidth = canvasElement.width;
stageHeight = canvasElement.height;
for (var i = 0; i < ballCount; i++) {
var nX = Math.random() * stageWidth;
var nY = Math.random() * stageHeight;
var velocityX = (Math.random() - 0.5) * 5;
var velocityY = (Math.random() - 0.5) * 5;
var ball = createBall(3, "black", nX, nY, velocityX, velocityY);
balls.push(ball);
stage.addChild(ball);
}
createjs.Ticker.addEventListener("tick", move);
}
function createBall(radius, color, nX, nY, velocityX, velocityY) {
var ball = new createjs.Shape();
drawBall(ball.graphics, radius, color);
ball.x = nX;
ball.y = nY;
ball.velocityX = velocityX;
ball.velocityY = velocityY;
return ball;
}
function drawBall(myGraphics, radius, color) {
myGraphics.beginFill(color);
myGraphics.drawCircle(0, 0, radius);
}
function move(eventObject) {
for (var i = 0; i < ballCount; i++) {
var ball = balls[i];
var nX = ball.x;
var nY = ball.y;
nX += ball.velocityX;
nY += ball.velocityY;
ball.x = roll(nX, stageWidth);
ball.y = roll(nY, stageHeight);
}
for (i = 0; i < ballCount - 1; i++) {
var ball0 = balls[i];
for (var j = i + 1; j < ballCount; j++) {
var ball1 = balls[j];
spring(ball0, ball1);
}
}
stage.update();
}
function roll(value, length) {
if (value > length) {
value -= length;
} else if (value < 0) {
value += length;
}
return value;
}
function spring(object0, object1) {
var distanceX = object1.x - object0.x;
var distanceY = object1.y - object0.y;
var squareX = distanceX * distanceX;
var squareY = distanceY * distanceY;
if (squareX + squareY < limit) {
var accelX = distanceX * ratio;
var accelY = distanceY * ratio;
object0.velocityX += accelX;
object0.velocityY += accelY;
object1.velocityX -= accelX;
object1.velocityY -= accelY;
}
}引合うオブジェクト同士の直線で結んでみる
つぎは、
var colorInt = 0x0;
var background = new createjs.Shape();
function initialize() {
var color = createjs.Graphics.getRGB(colorInt);
stage.addChild(background);
for (var i = 0; i < ballCount; i++) {
// var ball = createBall(3, "black", nX, nY, velocityX, velocityY);
var ball = createBall(3, color, nX, nY, velocityX, velocityY);
}
}線の描画は、
線は力の働くオブジェクトの間に引くので、
function move(eventObject) {
background.graphics.clear();
for (i = 0; i < ballCount - 1; i++) {
for (var j = i + 1; j < ballCount; j++) {
spring(ball0, ball1);
}
}
stage.update();
}
function spring(object0, object1) {
var _0x = object0.x;
var _0y = object0.y;
var _1x = object1.x;
var _1y = object1.y;
// var distanceX = object1.x - object0.x;
// var distanceY = object1.y - object0.y;
var distanceX = _1x - _0x;
var distanceY = _1y - _0y;
if (squareX + squareY < limit) {
var color = createjs.Graphics.getRGB(colorInt);
drawLine(1, color, _0x, _0y, _1x, _1y);
}
}
function drawLine(stroke, color, beginX, beginY, endX, endY) {
var myGraphics = background.graphics;
myGraphics.setStrokeStyle(stroke);
myGraphics.beginStroke(color);
myGraphics.moveTo(beginX, beginY);
myGraphics.lineTo(endX, endY);
}これで、
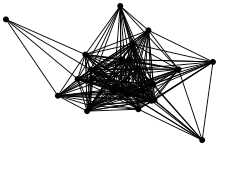
var stage;
var stageWidth;
var stageHeight;
var balls = [];
var ballCount = 25;
var ratio = 1 / 2000;
var limit = 100 * 100;
var colorInt = 0x0;
var background = new createjs.Shape();
function initialize() {
var color = createjs.Graphics.getRGB(colorInt);
var canvasElement = document.getElementById("myCanvas");
stage = new createjs.Stage(canvasElement);
stageWidth = canvasElement.width;
stageHeight = canvasElement.height;
stage.addChild(background);
for (var i = 0; i < ballCount; i++) {
var nX = Math.random() * stageWidth;
var nY = Math.random() * stageHeight;
var velocityX = (Math.random() - 0.5) * 5;
var velocityY = (Math.random() - 0.5) * 5;
var ball = createBall(3, color, nX, nY, velocityX, velocityY);
balls.push(ball);
stage.addChild(ball);
}
createjs.Ticker.addEventListener("tick", move);
}
function createBall(radius, color, nX, nY, velocityX, velocityY) {
var ball = new createjs.Shape();
drawBall(ball.graphics, radius, color);
ball.x = nX;
ball.y = nY;
ball.velocityX = velocityX;
ball.velocityY = velocityY;
return ball;
}
function drawBall(myGraphics, radius, color) {
myGraphics.beginFill(color);
myGraphics.drawCircle(0, 0, radius);
}
function move(eventObject) {
for (var i = 0; i < ballCount; i++) {
var ball = balls[i];
var nX = ball.x;
var nY = ball.y;
nX += ball.velocityX;
nY += ball.velocityY;
ball.x = roll(nX, stageWidth);
ball.y = roll(nY, stageHeight);
}
background.graphics.clear();
for (i = 0; i < ballCount - 1; i++) {
var ball0 = balls[i];
for (var j = i + 1; j < ballCount; j++) {
var ball1 = balls[j];
spring(ball0, ball1);
}
}
stage.update();
}
function roll(value, length) {
if (value > length) {
value -= length;
} else if (value < 0) {
value += length;
}
return value;
}
function spring(object0, object1) {
var _0x = object0.x;
var _0y = object0.y;
var _1x = object1.x;
var _1y = object1.y;
var distanceX = _1x - _0x;
var distanceY = _1y - _0y;
var squareX = distanceX * distanceX;
var squareY = distanceY * distanceY;
if (squareX + squareY < limit) {
var color = createjs.Graphics.getRGB(colorInt);
var accelX = distanceX * ratio;
var accelY = distanceY * ratio;
object0.velocityX += accelX;
object0.velocityY += accelY;
object1.velocityX -= accelX;
object1.velocityY -= accelY;
drawLine(1, color, _0x, _0y, _1x, _1y);
}
}
function drawLine(stroke, color, beginX, beginY, endX, endY) {
var myGraphics = background.graphics;
myGraphics.setStrokeStyle(stroke);
myGraphics.beginStroke(color);
myGraphics.moveTo(beginX, beginY);
myGraphics.lineTo(endX, endY);
}オブジェクトが離れるほど線を薄くする
粒子を見やすくするには、
すると改めて、
アルファは、
var max = 100;
// var limit = 100 * 100;
var limit = max * max;
function spring(object0, object1) {
if (squareX + squareY < limit) {
var distance = Math.sqrt(squareX + squareY);
var color = createjs.Graphics.getRGB(colorInt, (max - distance) / max);
drawLine(1, color, _0x, _0y, _1x, _1y);
}
}これで、
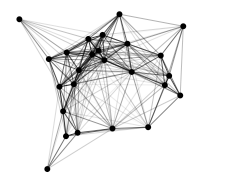
var stage;
var stageWidth;
var stageHeight;
var balls = [];
var ballCount = 25;
var ratio = 1 / 2000;
var max = 100;
var limit = max * max;
var colorInt = 0x0;
var background = new createjs.Shape();
function initialize() {
var color = createjs.Graphics.getRGB(colorInt);
var canvasElement = document.getElementById("myCanvas");
stage = new createjs.Stage(canvasElement);
stageWidth = canvasElement.width;
stageHeight = canvasElement.height;
stage.addChild(background);
for (var i = 0; i < ballCount; i++) {
var nX = Math.random() * stageWidth;
var nY = Math.random() * stageHeight;
var velocityX = (Math.random() - 0.5) * 5;
var velocityY = (Math.random() - 0.5) * 5;
var ball = createBall(3, color, nX, nY, velocityX, velocityY);
balls.push(ball);
stage.addChild(ball);
}
createjs.Ticker.addEventListener("tick", move);
}
function createBall(radius, color, nX, nY, velocityX, velocityY) {
var ball = new createjs.Shape();
drawBall(ball.graphics, radius, color);
ball.x = nX;
ball.y = nY;
ball.velocityX = velocityX;
ball.velocityY = velocityY;
return ball;
}
function drawBall(myGraphics, radius, color) {
myGraphics.beginFill(color);
myGraphics.drawCircle(0, 0, radius);
}
function move(eventObject) {
for (var i = 0; i < ballCount; i++) {
var ball = balls[i];
var nX = ball.x;
var nY = ball.y;
nX += ball.velocityX;
nY += ball.velocityY;
ball.x = roll(nX, stageWidth);
ball.y = roll(nY, stageHeight);
}
background.graphics.clear();
for (i = 0; i < ballCount - 1; i++) {
var ball0 = balls[i];
for (var j = i + 1; j < ballCount; j++) {
var ball1 = balls[j];
spring(ball0, ball1);
}
}
stage.update();
}
function roll(value, length) {
if (value > length) {
value -= length;
} else if (value < 0) {
value += length;
}
return value;
}
function spring(object0, object1) {
var _0x = object0.x;
var _0y = object0.y;
var _1x = object1.x;
var _1y = object1.y;
var distanceX = _1x - _0x;
var distanceY = _1y - _0y;
var squareX = distanceX * distanceX;
var squareY = distanceY * distanceY;
if (squareX + squareY < limit) {
var distance = Math.sqrt(squareX + squareY);
var color = createjs.Graphics.getRGB(colorInt, (max - distance) / max);
var accelX = distanceX * ratio;
var accelY = distanceY * ratio;
object0.velocityX += accelX;
object0.velocityY += accelY;
object1.velocityX -= accelX;
object1.velocityY -= accelY;
drawLine(1, color, _0x, _0y, _1x, _1y);
}
}
function drawLine(stroke, color, beginX, beginY, endX, endY) {
var myGraphics = background.graphics;
myGraphics.setStrokeStyle(stroke);
myGraphics.beginStroke(color);
myGraphics.moveTo(beginX, beginY);
myGraphics.lineTo(endX, endY);
}「Node Garden」



