前回は、
軌跡の描き方をお題と比べる
まず、
ドラッグを始めるリスナー関数
var wipingShape;
var oldPoint = new createjs.Point();
function startWipe(eventObject) {
var mousePoint = getMousePoint();
oldPoint.x = mousePoint.x;
oldPoint.y = mousePoint.y;
wipingShape.graphics
.setStrokeStyle(radius * 2, "round", "round");
}
function wipe(eventObject) {
var mousePoint = getMousePoint();
var mouseX = mousePoint.x;
var mouseY = mousePoint.y;
wipingShape.graphics
.beginStroke(createjs.Graphics.getRGB(0x0, 0.15))
.moveTo(oldPoint.x, oldPoint.y)
.lineTo(mouseX, mouseY);
oldPoint.x = mouseX;
oldPoint.y = mouseY;
}お題の
細かな中身はこれから順を追って説明する。だから、
var drawingCanvas;
var oldPt;
var oldMidPt;
function handleMouseDown(event) {
oldPt = new createjs.Point(stage.mouseX, stage.mouseY);
oldMidPt = oldPt;
}
function handleMouseMove(event) {
var midPoint = new createjs.Point(oldPt.x + stage.mouseX >> 1, oldPt.y+stage.mouseY >> 1);
drawingCanvas.graphics.setStrokeStyle(40, "round", "round")
.beginStroke("rgba(0,0,0,0.15)")
.moveTo(midPoint.x, midPoint.y)
.curveTo(oldPt.x, oldPt.y, oldMidPt.x, oldMidPt.y);
oldPt.x = stage.mouseX;
oldPt.y = stage.mouseY;
oldMidPt.x = midPoint.x;
oldMidPt.y = midPoint.y;
}2次ベジエ曲線を描く
Graphics.
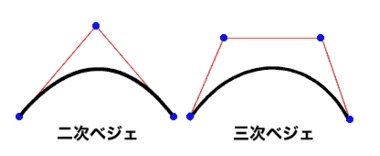
2次ベジエは、
Graphicsオブジェクト.quadraticCurveTo(コントロールx座標, コントロールy座標, 終点x座標, 終点y座標)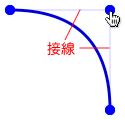
曲線の設定や引き始めの座標決めなどは、
Graphicsオブジェクト.beginStroke(カラー)
.setStrokeStyle(各スタイル, …)
.moveTo(始点x座標, 始点y座標)
.quadraticCurveTo(コントロールx座標, コントロールy座標, 終点x座標, 終点y座標);さて、
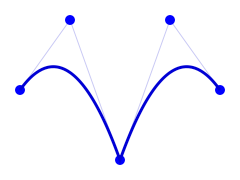
そこで、
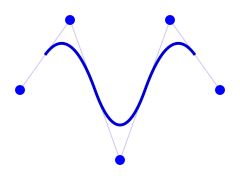
前項で確かめたお題の
2次ベジエ曲線で滑らかな軌跡を描く
それでは、
そして、
var oldPoint = new createjs.Point();
var oldMidPoint = new createjs.Point();
function startWipe(eventObject) {
var mousePoint = getMousePoint();
oldMidPoint.x = oldPoint.x = mousePoint.x;
oldMidPoint.y = oldPoint.y = mousePoint.y;
}
function wipe(eventObject) {
var mousePoint = getMousePoint();
var mouseX = mousePoint.x;
var mouseY = mousePoint.y;
var oldX = oldPoint.x;
var oldY = oldPoint.y;
var midX = (oldX + mouseX) / 2;
var midY = (oldY + mouseY) / 2;
wipingShape.graphics
.beginStroke(createjs.Graphics.getRGB(0x0, 0.15))
// .moveTo(oldPoint.x, oldPoint.y)
.moveTo(oldMidPoint.x, oldMidPoint.y)
// .lineTo(mouseX, mouseY);
.quadraticCurveTo(oldX, oldY, midX, midY);
oldPoint.x = mouseX;
oldPoint.y = mouseY;
oldMidPoint.x = midX;
oldMidPoint.y = midY;
}書き直したスクリプト全体は、
var stage;
var wipingShape;
var imageBitmap;
var blurBitmap;
var imageSize = new createjs.Point();
var radius = 10;
var bitmapPoint = new createjs.Point();
var oldPoint = new createjs.Point();
var oldMidPoint = new createjs.Point();
var isDrawing;
var cursor;
function initialize() {
var canvasElement = document.getElementById("myCanvas");
var canvasSize = new createjs.Point(canvasElement.width, canvasElement.height);
stage = new createjs.Stage(canvasElement);
var loader = new createjs.LoadQueue(false);
loader.addEventListener("fileload", draw);
loader.loadFile({
src: "images/image.png",
data: canvasSize
});
}
function draw(eventObject) {
var image = eventObject.result;
var canvasSize = eventObject.item.data;
var imageWidth = imageSize.x = image.width;
var imageHeight = imageSize.y = image.height;
var nX = bitmapPoint.x = (canvasSize.x - imageWidth) / 2;
var nY = bitmapPoint.y = (canvasSize.y - imageHeight) / 2;
stage.addEventListener("stagemousedown", startWipe);
stage.addEventListener("stagemouseup", stopWipe);
stage.enableMouseOver();
wipingShape = new createjs.Shape();
blurBitmap = createBitmap(image, nX, nY);
blurBitmap.filters = [new createjs.BoxBlurFilter(15, 15, 2)];
blurBitmap.cache(0, 0, imageWidth, imageHeight);
blurBitmap.alpha = 0.8;
imageBitmap = createBitmap(image, nX, nY);
createCursor();
updateCacheImage(false);
createjs.Ticker.addEventListener("tick", wipe);
}
function createBitmap(image, nX, nY) {
var myBitmap = new createjs.Bitmap(image);
myBitmap.x = nX;
myBitmap.y = nY;
stage.addChild(myBitmap);
return myBitmap;
}
function createCursor() {
cursor = new createjs.Shape();
cursor.graphics
.beginFill("white")
.drawCircle(0, 0, radius);
cursor.cursor = "pointer";
cursor.alpha = 0.3;
stage.addChild(cursor);
}
function startWipe(eventObject) {
var mousePoint = getMousePoint();
oldMidPoint.x = oldPoint.x = mousePoint.x;
oldMidPoint.y = oldPoint.y = mousePoint.y;
isDrawing = true;
wipingShape.graphics
.setStrokeStyle(radius * 2, "round", "round");
}
function wipe(eventObject) {
cursor.x = stage.mouseX;
cursor.y = stage.mouseY;
if (isDrawing) {
var mousePoint = getMousePoint();
var mouseX = mousePoint.x;
var mouseY = mousePoint.y;
var oldX = oldPoint.x;
var oldY = oldPoint.y;
var midX = (oldX + mouseX) / 2;
var midY = (oldY + mouseY) / 2;
wipingShape.graphics
.beginStroke(createjs.Graphics.getRGB(0x0, 0.15))
.moveTo(oldMidPoint.x, oldMidPoint.y)
.quadraticCurveTo(oldX, oldY, midX, midY);
oldPoint.x = mouseX;
oldPoint.y = mouseY;
oldMidPoint.x = midX;
oldMidPoint.y = midY;
updateCacheImage(true);
} else {
stage.update();
}
}
function stopWipe(event) {
isDrawing = false;
}
function getMousePoint() {
var mouseX = stage.mouseX - bitmapPoint.x;
var mouseY = stage.mouseY - bitmapPoint.y;
return new createjs.Point(mouseX, mouseY);
}
function updateCacheImage(update) {
updateCache(update, wipingShape);
var maskFilter = new createjs.AlphaMaskFilter(wipingShape.cacheCanvas);
imageBitmap.filters = [maskFilter];
updateCache(update, imageBitmap);
stage.update();
}
function updateCache(update, instance) {
if (update) {
instance.updateCache();
} else {
instance.cache(0, 0, imageSize.x, imageSize.y);
}
}
本当に滑らかな曲線が描けているのか
これでは腑に落ちない読者がおられよう。前掲コード1を試しても、
function draw(eventObject) {
createjs.Ticker.addEventListener("tick", wipe);
createjs.Ticker.setFPS(4);
}
function startWipe(eventObject) {
wipingShape.graphics
// .setStrokeStyle(radius * 2, "round", "round");
.setStrokeStyle(2);
}
function wipe(eventObject) {
wipingShape.graphics
// .beginStroke(createjs.Graphics.getRGB(0x0, 0.15))
.beginStroke(createjs.Graphics.getRGB(0x0))
.moveTo(oldMidPoint.x, oldMidPoint.y)
.quadraticCurveTo(oldX, oldY, midX, midY);
}前掲jsdo.
しかし、
もうひとつ謎が残っていた。お題の
JavaScriptも含めて多くのプログラミング言語は、
線を描いた後、
var oldPt;
var oldMidPt;
function handleMouseDown(event) {
oldPt = new createjs.Point(stage.mouseX, stage.mouseY);
oldMidPt = oldPt;
}
function handleMouseMove(event) {
drawingCanvas.graphics.setStrokeStyle(40, "round", "round")
.curveTo(oldPt.x, oldPt.y, oldMidPt.x, oldMidPt.y);
oldPt.x = stage.mouseX;
oldPt.y = stage.mouseY;
oldMidPt.x = midPoint.x;
oldMidPt.y = midPoint.y;
}奇しくも、



