第15回　Matrix2Dクラスで座標を回す

今回から取り組む新しいお題は、前回予告したつぎのjsdo.itのサンプルだ。ワイヤーフレームで描かれた星形を、3次元空間のy軸で回している。先に申し上げておくと、CreateJSに3次元座標を扱うクラスはない。2次元座標の変換を、3次元の考え方に応用してつくる。3次元空間の扱いには少し説明が要る。そのため、お題は3回くらいをかけて仕上げるつもりだ。なお、このjsdo.itのJavaScriptコードは、もう少し簡略化することになる。

星形を頂点座標と直線で描く

そういうことで、2次元平面の動かない星形から描いていこう（図1⁠）⁠。平面に星形を描いて終わりなら、EaselJSのGraphicsクラスにその名もGraphics.drawPolyStar()というメソッドがある（⁠「⁠EaselJSで描いた星形を回す」参照⁠）⁠。しかし、EaselJSのオブジェクトは3次元空間で回せない。そこでどうするかというと、3次元の頂点座標をオブジェクトでつくり、その回転を計算して描こうというもくろみだ。したがって、ここでは頂点をまずは2次元座標で定め、それらを直線で結んで星形にする。

描画の準備から先にしよう。座標の回転にはEaselJS 0.7.0の新しいメソッドを使う。script要素には最新版のライブラリを読み込んでおく。

<script src="http://code.createjs.com/easeljs-0.7.0.min.js"></script>

body要素に加えたcanvas要素にはid属性（"myCanvas"）を与え、初めに呼出す関数（initialize()）をonload属性で定めておくことはいつもどおりだ。描画はShapeインスタンスに行う。といっても、具体的にはShape.graphicsプロパティで参照するGraphicsオブジェクトに描くので、Shapeインスタンスはステージに置いた後触らない。そのため、変数（drawGraphics）には、Graphicsオブジェクトを直に納めることにする。

Shapeインスタンスは別の関数（createGraphics()）でつくる。引数に渡したxy座標で位置を定めたら、Stageオブジェクトの表示リストに加える。そして、前述の変数（drawGraphics）に与えるGraphicsオブジェクトを、Shapeインスタンスから取り出して返した。これで、ステージに新たなShapeインスタンスが置かれ、そのGraphicsオブジェクトの参照が変数に得られる。

var stage;
var drawGraphics;

function initialize() {
  var canvasElement = document.getElementById("myCanvas");
  stage = new createjs.Stage(canvasElement);
  drawGraphics = createGraphics(canvasElement.width / 2, canvasElement.height / 2);

}
function createGraphics(x, y) {
  var drawShape = new createjs.Shape();
  drawShape.x = x;
  drawShape.y = y;
  stage.addChild(drawShape);
  return drawShape.graphics;
}

つぎに、星形の頂点座標をPointオブジェクトでつくり、それらを配列に納める。そのための関数（createStarPoints()）をつぎのように定め、3つの引数で星のかたちを決められるようにしよう。3つの引数は、頂点数、および山と谷の半径だ（図2⁠）⁠。頂点は尖った山の数、半径は中心から山の頂点と谷の底までのそれぞれの長さで決める。

function createStarPoints(頂点数, 山の半径, 谷の半径)

原点(0, 0)は星の中心にとって、山と谷の点の座標をすべて求めたい。原点から求める点までの長さと、2点を結ぶ直線が正のx軸となす角度からxy座標はつぎのように導ける（第11回「マウスポインタの動きに合わせてインスタンスをランダムに落とす」「⁠インスタンスの動きに水平方向の初速を加える」参照⁠）⁠。

x = 距離×cos角度
y = 距離×sin角度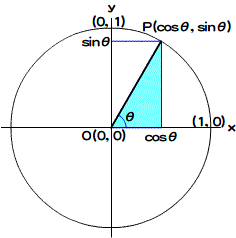

第11回図4　原点から距離が1で角度θのxy座標は（cosθ, sinθ） — **第11回図4**　原点から距離が1で角度θのxy座標は（cosθ, sinθ）（⁠再掲）

では、新たな関数（createStarPoints()）の3つの引数から、星形の山と谷の座標を求めてみよう。この関数は初期化の関数（initialize()）で呼出し、戻り値として座標のPointエレメントが納められた配列を受け取って、変数（points）に入れることとする。

星形の山と谷の各点と原点を結んだ中心角はすべて等しい。その角度（theta）は、引数の山の頂点数（numVertices）の2倍で1周の角度2π（360度）を割れば導ける。座標は星形のてっぺん、つまり12時方向の山の点からとる。その角度（angle）は-π/2（-90度）だ。そのうえで、角度（angle）はforループで増やしつつ、山と谷の点の座標を交互にPointオブジェクトにして配列（starPoints）に納める。すべての座標が求められたら、その配列を返せばよい。

var points;
function initialize() {

  points = createStarPoints(5, 65, 25);

}

function createStarPoints(numVertices, longRadius, shortRadius) {
  var starPoints = [];
  var angle = Math.PI;
  var theta = angle / numVertices;
  angle /= -2;
  for (var i = 0; i < numVertices; i++) {
    starPoints.push(new createjs.Point(longRadius * Math.cos(angle), longRadius * Math.sin(angle)));
    angle += theta;
    starPoints.push(new createjs.Point(shortRadius * Math.cos(angle), shortRadius * Math.sin(angle)));
    angle += theta;
  }
  return starPoints;
}

後は、配列（points）から座標を取出して、すべて直線で結ぶだけだ。その関数（draw()）も新たに定めて、初期化の関数から呼出す。引数はPointエレメントが納められた配列とする。すでにGraphicsオブジェクトは変数（drawGraphics）にとってあるので、そこに直線で星形を描く。

線描の関数（draw()）はGraphicsクラスのメソッドにより、Graphics.beginStroke()で線の色（"mediumblue"⁠）⁠、Graphics.setStrokeStyle()はその太さ（3）を定める。そして、Graphics.moveTo()が描き始めの座標を決めたら、forループで引数の配列から取り出したPointオブジェクトの座標を順にGraphics.lineTo()メソッドによって結べば星形が描かれる。

function initialize() {

  draw(points);
}

function draw(points) {
  var count = points.length;
  var point = points[count - 1];
  drawGraphics.clear()
  .beginStroke("mediumblue")
  .setStrokeStyle(3)
  .moveTo(point.x, point.y);
  for (var i = 0; i < count; i++) {
    point = points[i];
    drawGraphics.lineTo(point.x, point.y);
  }
  stage.update();
}

さて、上記コードで直線を描くforループの組立てにひとつ工夫がある。配列の始めのPointエレメントから描き始めるなら、その座標をGraphics.moveTo()メソッドで起点に定める。そうなると、最後のエレメントの座標までGraphics.lineTo()メソッドで直線を結んだ後、改めて起点まで戻って直線を描かないと一周しない。

しかし、上記のJavaScriptコードでは、描き始めの座標を配列の最後のPointエレメント（points[count - 1]）で決めた。すると、forループでは初めのPointエレメントから順に直線が描かれ、起点とした最後の座標まで結んだところで星はでき上がる。

もうひとつ補っておきたいのは、星形を描く前にGraphics.clear()メソッドを呼び出していることだ。まっさらなGraphicsオブジェクトには消す描画などない。だがこの後、星形をアニメーションさせるつもりだ。そのため、このメソッドの呼出しをすでに加えておいた。

ここまでをまとめたのがつぎのコード1だ。ステージの真ん中に5頂点の星形が直線で描かれる（前掲図1参照⁠）⁠。単純な線描とはいえ、座標から計算してつくった。したがって、考え方は3次元の描画にも応用できる。

コード1　星形の頂点座標を直線で結んで描く

var stage;
var drawGraphics;
var points;
function initialize() {
  var canvasElement = document.getElementById("myCanvas");
  stage = new createjs.Stage(canvasElement);
  drawGraphics = createGraphics(canvasElement.width / 2, canvasElement.height / 2);
  points = createStarPoints(5, 65, 25);
  draw(points);
}
function createGraphics(x, y) {
  var drawShape = new createjs.Shape();
  drawShape.x = x;
  drawShape.y = y;
  stage.addChild(drawShape);
  return drawShape.graphics;
}
function draw(points) {
  var count = points.length;
  var point = points[count - 1];
  drawGraphics.clear()
  .beginStroke("mediumblue")
  .setStrokeStyle(3)
  .moveTo(point.x, point.y);
  for (var i = 0; i < count; i++) {
    point = points[i];
    drawGraphics.lineTo(point.x, point.y);
  }
  stage.update();
}
function createStarPoints(numVertices, longRadius, shortRadius) {
  var starPoints = [];
  var angle = Math.PI;
  var theta = angle / numVertices;
  angle /= -2;
  for (var i = 0; i < numVertices; i++) {
    starPoints.push(new createjs.Point(longRadius * Math.cos(angle), longRadius * Math.sin(angle)));
    angle += theta;
    starPoints.push(new createjs.Point(shortRadius * Math.cos(angle), shortRadius * Math.sin(angle)));
    angle += theta;
  }
  return starPoints;
}

座標を回転して描く線のアニメーション

では、描いた星形を2次元平面で回そう。Shapeインスタンスそのものは、DisplayObject.rotationプロパティで回転角が定められる。けれど、今回はひとつひとつの座標を回したい。そのために用いるのが、EaselJS 0.7.0に新たに備わったMatrix2D.transformPoint()メソッドだ。第1および第2引数のxy座標をMatrix2Dオブジェクトで変換して、その結果の座標が第3引数のPointオブジェクトに与えられる。

Matrix2Dオブジェクト.transformPoint(x座標, y座標, Pointオブジェクト)

そのMatrix2Dとは何かというと、伸縮や回転、さらに移動といった座標の変換を数学的な情報としてもつオブジェクトだ[1]⁠。数学では行列（Matrix）で表されるため、この名がつけられた。Matrix2Dオブジェクトの座標を変換するメソッドは数多く備わっている。伸縮と回転および移動のメソッドはつぎの表1のとおりだ。

表1　Matrix2Dクラスの伸縮と回転および移動のメソッド

Matrix2Dクラスのメソッド	オブジェクトへの座標変換
scale()	Matrix2Dオブジェクトを、水平あるいは垂直に引数の比率伸縮する。
rotate()	Matrix2Dオブジェクトを、引数の角度(ラジアン)回転する。
translate()	Matrix2Dオブジェクトを、水平あるいは垂直に引数の座標移動する。

Matrix2Dオブジェクトの座標変換は、DisplayObjectインスタンスに加えられる（⁠「⁠EaselJSのMatrix2Dオブジェクトの変換行列を適用する」参照⁠）⁠。さらに、新たなMatrix2D.transformPoint()メソッドにより、Pointオブジェクトの座標も変換できるようになった。このメソッドで、前掲コード1の星形を回してみよう。

座標変換に使うMatrix2Dオブジェクトは、予め変数（matrix）に与える。Matrix2D()コンストラクタに引数を渡さないと、変換なしのデフォルトでオブジェクトがつくられる。また、インスタンスを回す角度（5度=π/36ラジアン）も変数（angle）に入れておく。そして、初期化の関数（initialize()）でTicker.tickイベントにリスナー（rotate()）を加える。

座標回転のリスナー関数（rotate()）は、予め定めた角度（angle）Matrix2D.rotate()メソッドでオブジェクトを回転する。そして、forループで配列から取出したPointエレメントすべての座標を、Matrix2D.transformPoint()メソッドで回す。そのうえで、線描の関数（draw()）を呼び出せば、直線で描かれる星形が回るアニメーションになる。

var angle = Math.PI / 36;
var matrix = new createjs.Matrix2D();
function initialize() {

  createjs.Ticker.addEventListener("tick", rotate);
}
function rotate(eventObject) {
  var count = points.length;
  matrix.identity().rotate(angle);
  for (var i = 0; i < count; i++) {
    var point = points[i];
    matrix.transformPoint(point.x, point.y, point);
  }
  draw(points);
}

なお、Matrix2D.identity()メソッドは、参照するMatrix2Dオブジェクトを変換なしのデフォルト状態にする。新たなオブジェクトをつくるより使い回す方がお得なのは前回述べたとおりだ。もっとも、回転する角度（angle）が同じなら、そのまま使い続ければ済む。これは、この後回転角をマウスポインタの位置によって変えることに備えて加えた。

これで、Matrix2DクラスのメソッドによりPointオブジェクトの座標は回転し、直線で描かれる星形が回るアニメーションになる。手を加えたスクリプト全体は、つぎのコード2のとおりだ。

コード2　座標を回転して描く星形のアニメーション

var stage;
var drawGraphics;
var points;
var angle = Math.PI / 36;
var matrix = new createjs.Matrix2D();
function initialize() {
  var canvasElement = document.getElementById("myCanvas");
  stage = new createjs.Stage(canvasElement);
  drawGraphics = createGraphics(canvasElement.width / 2, canvasElement.height / 2);
  points = createStarPoints(5, 65, 25);
  draw(points);
  createjs.Ticker.addEventListener("tick", rotate);
}
function rotate(eventObject) {
  var count = points.length;
  matrix.identity().rotate(angle);
  for (var i = 0; i < count; i++) {
    var point = points[i];
    matrix.transformPoint(point.x, point.y, point);
  }
  draw(points);
}
function createGraphics(x, y) {
  var drawShape = new createjs.Shape();
  drawShape.x = x;
  drawShape.y = y;
  stage.addChild(drawShape);
  return drawShape.graphics;
}
function draw(points) {
  var count = points.length;
  var point = points[count - 1];
  drawGraphics.clear()
  .beginStroke("mediumblue")
  .setStrokeStyle(3)
  .moveTo(point.x, point.y);
  for (var i = 0; i < count; i++) {
    point = points[i];
    drawGraphics.lineTo(point.x, point.y);
  }
  stage.update();
}
function createStarPoints(numVertices, longRadius, shortRadius) {
  var starPoints = [];
  var angle = Math.PI;
  var theta = angle / numVertices;
  angle /= -2;
  for (var i = 0; i < numVertices; i++) {
    starPoints.push(new createjs.Point(longRadius * Math.cos(angle), longRadius * Math.sin(angle)));
    angle += theta;
    starPoints.push(new createjs.Point(shortRadius * Math.cos(angle), shortRadius * Math.sin(angle)));
    angle += theta;
  }
  return starPoints;
}

アニメーションの回転をマウスポインタの水平位置に応じて変える

前掲コード2で、回転角の変数（angle）の値は動的に変えられる。今回の仕上げとして、マウスポインタの水平位置に応じて、星形の回る向きと速さを動的に変えてみよう。ステージの水平位置中央を基準として、マウスポインタがその左右どちらにあるかによって回る方向を決め、離れた距離に比例して速さを増す。

初期化の関数（initialize()）で、ステージ中央の水平座標値は変数（stageCenterX）にとる。そして、Stage.stagemousemoveイベントにリスナー（setAngle()）を加える。リスナー関数は、マウスポインタとステージ中央の水平座標の差に比例した角度を変数に与える。なお、引数に受取ったイベントオブジェクトのMouseEvent.stageXとMouseEvent.stageYプロパティでポインタの座標は調べられる。

var stageCenterX;
function initialize() {

  stageCenterX = canvasElement.width / 2;
  // drawGraphics = createGraphics(canvasElement.width / 2, canvasElement.height / 2);
  drawGraphics = createGraphics(stageCenterX, canvasElement.height / 2);

  stage.addEventListener("stagemousemove", setAngle);
}
function setAngle(eventObject) {
  var mouseX = eventObject.stageX;
  angle = (mouseX - stageCenterX) * 1 / 300;
}

これで、マウスポインタの水平位置に応じて、星形の回る向きと速さが動的に変わる。ここまでの手を加えたのが、つぎのコード3だ。jsdo.itにもサンプルを掲げた。次回はさらにz座標を加えて、y軸で回してみたい。

コード3　マウスポインタの水平位置に応じてアニメーションが回る向きと速さを変える

var stage;
var drawGraphics;
var points;
var angle = Math.PI / 36;
var matrix = new createjs.Matrix2D();
var stageCenterX;
function initialize() {
  var canvasElement = document.getElementById("myCanvas");
  stage = new createjs.Stage(canvasElement);
  stageCenterX = canvasElement.width / 2;
  drawGraphics = createGraphics(stageCenterX, canvasElement.height / 2);
  points = createStarPoints(5, 65, 25);
  draw(points);
  createjs.Ticker.addEventListener("tick", rotate);
  stage.addEventListener("stagemousemove", setAngle);
}
function setAngle(eventObject) {
  var mouseX = eventObject.stageX;
  angle = (mouseX - stageCenterX) * 1 / 300;
}
function rotate(eventObject) {
  var count = points.length;
  matrix.identity().rotate(angle);
  for (var i = 0; i < count; i++) {
    var point = points[i];
    matrix.transformPoint(point.x, point.y, point);
  }
  draw(points);
}
function createGraphics(x, y) {
  var drawShape = new createjs.Shape();
  drawShape.x = x;
  drawShape.y = y;
  stage.addChild(drawShape);
  return drawShape.graphics;
}
function draw(points) {
  var count = points.length;
  var point = points[count - 1];
  drawGraphics.clear()
  .beginStroke("mediumblue")
  .setStrokeStyle(3)
  .moveTo(point.x, point.y);
  for (var i = 0; i < count; i++) {
    point = points[i];
    drawGraphics.lineTo(point.x, point.y);
  }
  stage.update();
}
function createStarPoints(numVertices, longRadius, shortRadius) {
  var starPoints = [];
  var angle = Math.PI;
  var theta = angle / numVertices;
  angle /= -2;
  for (var i = 0; i < numVertices; i++) {
    starPoints.push(new createjs.Point(longRadius * Math.cos(angle), longRadius * Math.sin(angle)));
    angle += theta;
    starPoints.push(new createjs.Point(shortRadius * Math.cos(angle), shortRadius * Math.sin(angle)));
    angle += theta;
  }
  return starPoints;
}