今回のお題は、animationプロパティを使った。といっても、
五角柱をつくる計算
今回の表現は、transformプロパティだ。関数rotateY()とtranslateZ()で、
四角柱は、rotateY()関数)。すると、translateZ()関数)。なお、
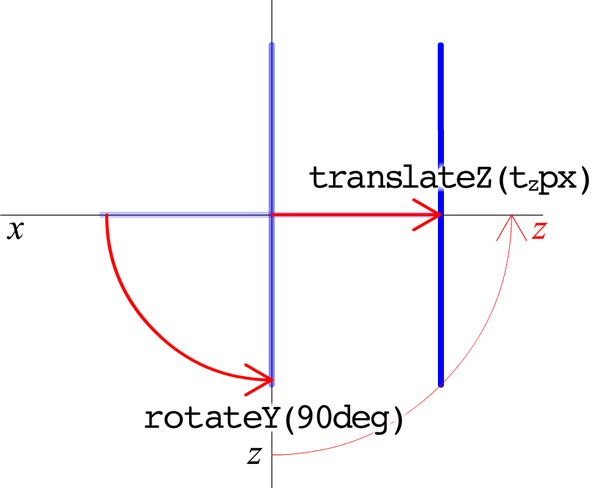
五角柱もそれぞれの面をy軸で回してrotateY()関数)、translateZ()関数)
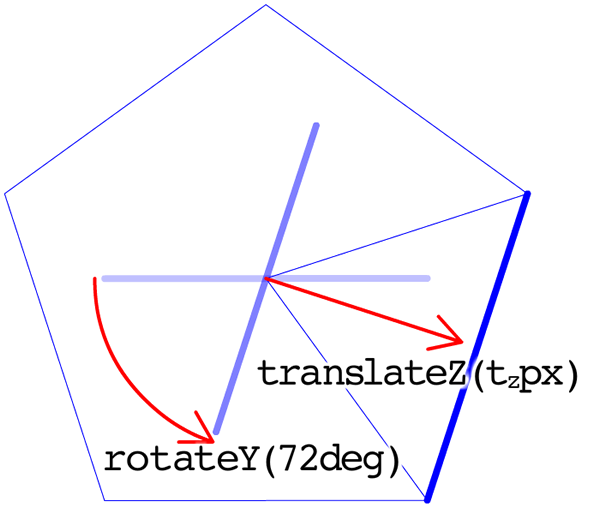
この場合、
tanθ= 高さ / 底辺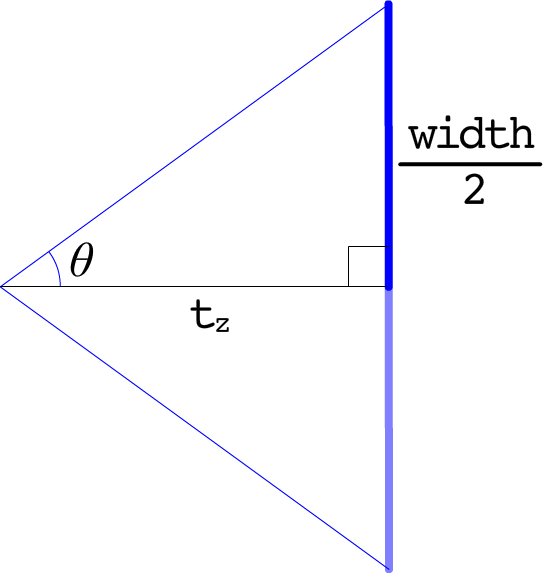
さて、<body>要素の記述は以下のコード1のとおりで、img要素)widthプロパティ)<img>要素に揃えて240ピクセルを与えたので、
tanθ = (width / 2) / tz
tz = (width / 2) / tanθ
= 120 / tan(36°)<body>要素の記述<div class="container">
<div class="spinner">
<img class="face face-1" src="images/pen01.png" width="240" height="160" alt="面1">
<img class="face face-2" src="images/pen02.png" width="240" height="160" alt="面2">
<img class="face face-3" src="images/pen03.png" width="240" height="160" alt="面3">
<img class="face face-4" src="images/pen04.png" width="240" height="160" alt="面4">
<img class="face face-5" src="images/pen05.png" width="240" height="160" alt="面5">
</div>
</div>もっとも、Math.メソッドにより得られる。ただし、Math.定数で表される。コンソールにつぎのように入力したら、
120 / Math.tan(Math.PI / 5)
五角柱を組み立てる
それでは、
.container {
margin: 1em auto;
padding: 1em;
width: 240px;
height: 160px;
}
.spinner img {
position: absolute;
border: 1px solid #ccc;
background: rgba(255, 255, 255, 0.8);
box-shadow: inset 0 0 20px rgba(0, 0, 0, 0.2);
}3次元の表現を加えるには、transform-styleにpreserve-3dを与え、perspectiveの値が定められていなければならない
.container {
perspective: 1200px;
}
.spinner {
transform-style: preserve-3d;
}
.face {
padding: 0px 7px;
}
.face-1 {
transform: /* rotateY(0deg) */ translateZ(175px);
}
.face-2 {
transform: rotateY(72deg) translateZ(175px);
}
.face-3 {
transform: rotateY(144deg) translateZ(175px);
}
.face-4 {
transform: rotateY(216deg) translateZ(175px);
}
.face-5 {
transform: rotateY(288deg) translateZ(175px);
}面のz軸方向の位置は少し遠めpaddingプロパティに左右の余白を定めた
tanθ = (width / 2) / tz
width = 2tztanθこれで、

.container {
margin: 1em auto;
padding: 1em;
perspective: 1200px;
width: 240px;
height: 160px;
}
.spinner {
transform-style: preserve-3d;
}
.spinner img {
position: absolute;
border: 1px solid #ccc;
background: rgba(255, 255, 255, 0.8);
box-shadow: inset 0 0 20px rgba(0, 0, 0, 0.2);
}
.face {
padding: 0px 7px;
}
.face-1 {
transform: translateZ(175px);
}
.face-2 {
transform: rotateY(72deg) translateZ(175px);
}
.face-3 {
transform: rotateY(144deg) translateZ(175px);
}
.face-4 {
transform: rotateY(216deg) translateZ(175px);
}
.face-5 {
transform: rotateY(288deg) translateZ(175px);
}五角柱を水平に回す
いよいよアニメーションを定める。もっとも、animationの使い方は、transitionと同じで、transitionと変わらない。繰り返し回数が与えられるのは、animationプロパティのよいところだ。繰り返し続けたいときは、infiniteとする。一番の違いは、
animation: 時間 タイミング関数 繰り返し回数 アニメーション名今回は、animationプロパティを指定した。タイミング関数linearは、
.spinner {
animation: 6s linear infinite spinner;
}アニメーション名は@keyframes規則に与える。transitionプロパティは、@keyframes規則には、fromおよびtoというキーワードを用いてもよい。
@keyframes アニメーション名 {
キーフレーム {
/* プロパティの定め */
}
}もっとも今回は、
@keyframes spinner {
/* from {
transform: rotateY(0deg);
} */
to {
transform: rotateY(-360deg);
}
}アニメーションのために加えたコードがあっけないほど簡単だったので、animation-play-stateだ。つぎのように、pausedを与えるとアニメーションは一時停止する。デフォルト値は、runningになっている。書き上がったCSSの定めは、
.spinner:hover {
animation-play-state: paused;
}.container {
margin: 1em auto;
padding: 1em;
perspective: 1200px;
width: 240px;
height: 160px;
}
.spinner {
animation: 6s linear infinite spinner;
transform-style: preserve-3d;
}
@keyframes spinner {
to {
transform: rotateY(-360deg);
}
}
.spinner:hover {
animation-play-state: paused;
}
.spinner img {
position: absolute;
border: 1px solid #ccc;
background: rgba(255, 255, 255, 0.8);
box-shadow: inset 0 0 20px rgba(0, 0, 0, 0.2);
}
.face {
padding: 0px 7px;
}
.face-1 {
transform: translateZ(175px);
}
.face-2 {
transform: rotateY(72deg) translateZ(175px);
}
.face-3 {
transform: rotateY(144deg) translateZ(175px);
}
.face-4 {
transform: rotateY(216deg) translateZ(175px);
}
.face-5 {
transform: rotateY(288deg) translateZ(175px);
}


