UNIXの基本的なコマンドの1つであるdiff。
これに実装されているアルゴリズムは実に興味深い世界が広がっています。
本稿では、筆者が開発した独自ライブラリ「dtl」をもとに「diffのしくみ」を解説します。
本記事は、Software Design 2009年6月号の記事を、現在の状態に合わせて加筆/修正しています。
はじめに
diffは2つのファイルやディレクトリの差分を取るのに使用するプログラムです。
ソフトウェア開発を行っている方であれば、SubversionやGitなどのバージョン管理システムを通して利用していることが多いかと思います。本稿ではそのdiffの動作原理について解説します。
差分の計算の際に重要な3つの要素
差分を計算するというのは次の3つを計算することに帰結します。
- 編集距離
- 2つの要素列の違いを数値化したもの
- LCS(Longest Common Subsequence)
- 2つの要素列の最長共通部分列
- SES(Shortest Edit Script)
- ある要素列を別の要素列に変換するための最短手順
dtlを使って文字列の差分を計算する
本稿ではdtlというdiffライブラリとそのサンプルプログラムを利用して、これらの用語について具体的に解説します。dtlはdiff template libraryの略で、筆者が開発しているC++製のdiffライブラリです[1]。
dtlのサンプルプログラムのビルドにはSCons[2]を使用しているので、まずはSConsをインストールしてください。DebianやUbuntuであれば次のコマンドでインストールできます。
$ sudo aptitude install scons
また、C++プログラムをコンパイルするために、次のパッケージもインストールします。
$ sudo aptitude install build-essential
その後、次のコマンドを実行してください。
$ wget http://dtl-cpp.googlecode.com/files/dtl-1.12.tar.gz
$ tar zxvf dtl-1.12.tar.gz
$ cd dtl-1.12/examples
$ scons strdiff
これで準備が整いました。dtlのサンプルプログラムの1つであるstrdiffを使って2つの文字列の差分を計算してみます。
たとえば、「abcdef」と「dacfea」という文字列があるとしましょう。strdiffにこの2つの文字列を引数として与えて実行すると、図1のようにeditDistance(編集距離)、LCS、SESを計算してその結果を出力してくれます。
図1 strdiffの実行結果
$ ./strdiff abcdef dacfea
editDistance:6
LCS:acf
SES
+ d
a
- b
c
- d
- e
f
+ e
+ a
まず、①のeditDistance(編集距離)の説明からいきたいところですが、これは③のSESと関連するため、先に②のLCSについて解説し、そのあとで残りの2つをまとめて解説します。
LCS(Longest Common Subsequence)
LCSは最長共通部分列であると書きましたが、単に2つの要素列に共通して含まれる要素の列ではなく、2つの要素列の中で共通する部分で最も長い列を指します。つまり、LCSはつねに連続しているわけではありませんが、もとの要素列の順序どおりに並んでいる必要があります。これはどういうことかと言うと、「abcdef」と「dacfea」に共通して含まれる文字は「a」、「c」、「d」、「e」、「f」の5つになります。これに対して、図1の結果を見ると、2つの文字列「abcdef」と「dacfea」のLCSは「acf」でした。
「d」と「e」がLCSに含まれていないのは、この2つの文字がLCSに含まれてしまうと、もとの文字列のどちらかの順序どおりに並ばなくなるからです。
たとえば、要素「d」は文字列「abcdef」では、LCSの要素である「a」と「c」よりも後ろに出現し、そのあとは出現しません。これに対して文字列「dacfea」では「a」と「c」よりも前にだけ出現します。
「e」と「f」についても、「abcdef」と「dacfea」とでは順序が逆になってしまうため、両方がLCSに含まれることはあり得ません。逆に、片方だけが含まれるLCSは存在します。というのも、図1の結果ではLCSは「acf」になっていますが、「ace」もまたLCSです。「acf」も「ace」も長さは3で同じなので、どちらもLCSであると言えます。
このように、LCSはつねに1つとは限りません。また、LCSが変わると後述するSESも変わってしまうので、注意が必要です。
SES(Shortest Edit Script)
図1の結果からSESは③のようになりました。SESは先述したように「ある要素列を別の要素列に変換するための最短手順」を表します。つまり、③は「abcdef」という文字列を「dacfea」という文字列に変換するための最短手順を表しています。ふだんdiffを使っている人にとっては、これが一番なじみの深いものではないかと思います。③のSESをもう少し詳細にすると、表1のようになります。
表1 abcdefからdacfeaへのSES
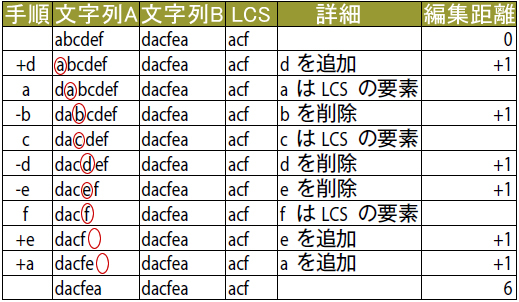
- 「追加」の場合はマークしている文字の前に追加対象の文字を追加
- 「削除」の場合はマークしている文字を削除
- 「LCSの要素」の場合はマークしている文字から右に一文字進める
編集距離
表1から読み取れるように編集距離とはSESにおける要素の「追加」と「削除」の合計を表しています。図1の①を見るとeditDistance(編集距離)は6ですので、計算どおりです。
効率的な差分アルゴリズム
差分の計算をするには「編集距離」「LCS」「SES」を求めれば良いということがわかりました。しかし、差分の計算というのは非常に重い処理で、単純に2つの要素列を比較するようなプログラムでは、計算量がO(MN)、必要なメモリがM×Nになってしまいます注3。そのため、実用的なdiffのプログラムには計算量や計算に必要なメモリの量を小さくする工夫が求められます。ここでは効率的なアルゴリズムの1つであり、dtlやSubversionで使用されているWuのアルゴリズムについて解説します。
Wuのアルゴリズム
Wuのアルゴリズムは平均的な計算量がO(N+PD)、最悪の計算量がO(NP)であるアルゴリズムで、Nは2つの要素列の長さの和、PはSESにおける「削除」の合計数を表しています注4。
エディットグラフと最短経路問題
Wuのアルゴリズムの基本的な考え方は、差分を計算するという問題を2つの要素列を図2のように、エディットグラフと呼ばれるグラフに見立てて、点(0,0)から点(M,N)注5までの(ある条件つきの)最短経路を求める問題に還元することにあります。言葉で説明するよりも図で説明したほうがわかりやすいと思うので、図2を見てください。
図2 エディットグラフ※エディットグラフは、xを縦軸、yを横軸でよく扱うので、本稿でもそれに従っています。
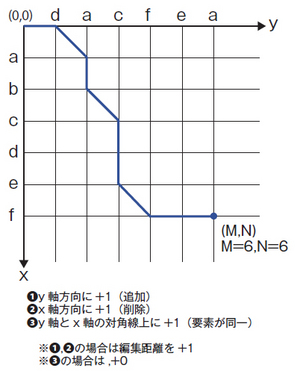
図のように、SESにおける「追加」を「y軸方向に+1」、「削除」を「x軸方向に+1」、また、互いの要素列の現在の要素が同一の場合、「y軸とx軸の対角線上に+1」というふうに定義します。そして「y軸方向に+1」、もしくは「x軸方向に+1」進むのに必要なコストを1、「y軸とx軸の対角線上に+1」進むのに必要なコストを0とします。このように考えると、2つの要素列の差分を計算するというのは、図2のようなエディットグラフの点(0,0)から点(M,N)まで進むのに必要なコストを最小限にする経路(SES)を求めることと等価だと考えることができます。
Wuのアルゴリズムの動作原理
エディットグラフ上の最短経路を求めれば差分を計算できることがわかりました。
では、どのようにして最短経路を計算するのでしょうか。単純に1つひとつ総当たりで調べていくアルゴリズムだと、計算量はO(MN)、またエディットグラフを表すデータ構造(たとえばM×Nの2次元配列)のためにM×Nのメモリが必要になります。
Wuのアルゴリズムは計算量が最悪の場合でもO(NP)、また平均的な計算量がO(N+PD)となるので、かなりの改善が期待できます。それでは、このような少ない計算量を実現しているWuのアルゴリズムがどのように動作しているのか解説していきます注6。
D=Δ+2P(※Δはデルタ)
まず、次のような約束事をします。
- 2つの要素列の長さをM、N(N≧M)とし、Δ=N-Mとする
- 編集距離をDとする
- SESにおける「削除」の合計数をPとする
Δは2つの要素列の長さだけがわかっている際に、考えられる最小編集距離です。これは図3のよう考えるとわかりやすいと思います。
図3のように、片方の要素列が2つの要素列のLCSと完全に一致する場合(図3の例では「abc」)、編集距離はΔ=N-M(N≧M)で表すことができます。
図3 Δ=Dとなる場合のエディットグラフ
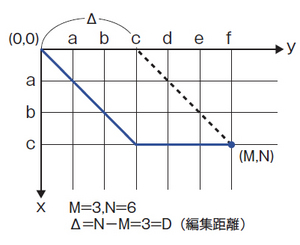
つまり、どんなにがんばっても編集距離はΔよりも小さい値にはならないわけです。
しかしそれ以外の場合、たとえば、「abec」と「abcdef」の場合、図4のように編集距離はΔよりも大きくなります。
図4 LCSとSESを求める
$ ./strdiff abec abcdef
editDistance:4
LCS:abe
SES
a
b
+ c
+ d
e
+ f
- c
この場合のエディットグラフを図5に示します。先述したように2つの要素列の長さだけからわかる最小の編集回数はΔです。
図5 Δ≠Dとなる場合のエディットグラフ
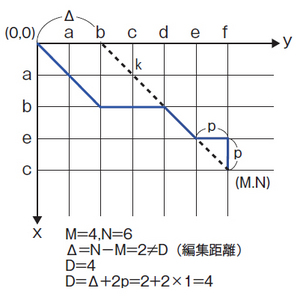
たとえばy軸方向へΔだけ進んだあとに(0,Δ)から(M,N)までの対角線k上を一気に進むことができれば、編集距離はΔになります。しかし、そうならない場合、対角線kの上側(下側)を通ることになります。ここで、エディットグラフ上のある性質が見てとれます。それは対角線k上からPだけy軸(x軸)方向に進んだ場合、最終的に点(M,N)にたどり着くには対角線k上に復帰する必要があるので、Pだけx軸(y軸)方向に進まなければならないということです。
また、対角線k上の点にたどり着くには最低でもコストがΔかかります。よって次の関係が成り立ちます。
探索範囲を絞り込む
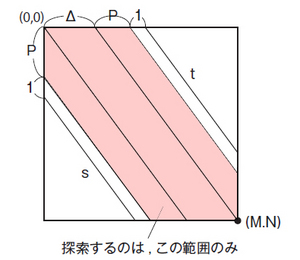
先ほど述べたように単純にひとつひとつ総当たりで調べていくのでは、計算量が大きくなってしまいます。そこで、Wuのアルゴリズムでは経路の探索範囲を図6のように絞り込むことによって、計算量を大幅に削減しています。このような絞り込みができるのは、最短経路がこの範囲外にある場合、「削除」の合計数Pの値が矛盾してしまうためです。
たとえば、図6のように対角線s上を通る経路では、どうがんばってもP=P+1となってしまいます。また、対角線t上を通る経路でも同様です。
図6 探索範囲の絞り込み
探索の仕方
まず、図7のように各点への対角線kをy-xと定義します。
図7 エディットグラフで対角線kを定義する
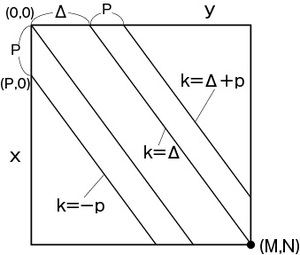
たとえば、点(M,N)や(M-1,N-1)だとk=Δ、点(P,0)だとk=-P、点(0,Δ+P)だとk=Δ+Pになります。
このように-P≦k≦Δ+Pを探索範囲、P=pの場合の各対角線k上における到達可能な最遠点をfp(k,p)、任意の点(x,y)から到達可能な最遠点fp(k,p)注7を計算する関数をsnake(k,y)と定義します。
図8と図9に対角線k-1、k、k+1とそれぞれの最遠点fp(k-1,p')、fp(k,p)、fp(k+1,p'')注8との関係を示します。
図8 fp(k,p)=snake(k,fp(k-1,p"))
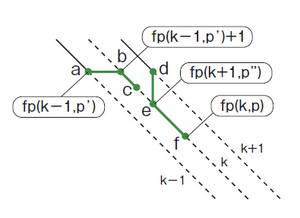 図9 fp(k,p)=snake(k,fp(k-1,p')+1))
図9 fp(k,p)=snake(k,fp(k-1,p')+1))
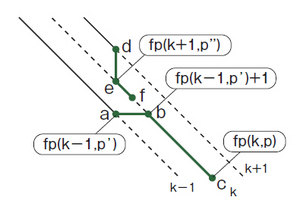
図8は対角線k+1の最遠点fp(k+1,p'')から対角線上に進む経路がfp(k,p)として採用される場合、つまり、fp(k,p)=snake(k,fp(k+1,p''))となることを、図9は対角線k-1の最遠点fp(k-1,p')+1から対角線上に進む経路がfp(k,p)として採用される場合、つまり、fp(k,p)=snake(k,fp(k-1,p')+1となることを示しています。
このことからfp(k,p)の値はk=Δを境にsnakeを使って図10のように式で表すことができます。
図10 snake関数とfp(k,p)の関係

最終的に、kの取り得る値の範囲を探索してfp(Δ,p)の値がNになったとき、点(M,N)に到達したことになるので、このときのpの値が、SESにおける「削除」の合計数Pになります。D=Δ+2Pなので、これで編集距離が求まります。fp(Δ,p)<Nの場合はpの値(初期値は0)をインクリメントして、同じことを繰り返します。
また、LCSやSESを求めるにはいろいろ方法がありますが、たとえば探索途中(snake関数内)で使うx、yおよびどの最遠点を通過したかという情報を記録することによって求めることができます。
Wuのアルゴリズムを使ったサンプルプログラム
以上のことをもとに、実際にWuのアルゴリズムを使って引数として与えられた2つの文字列間の編集距離を求めるC++プログラムをリスト1に示します。
リスト1 文字間の編集距離を求めるプログラム
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
class Diff
{
public :
Diff(const string &a, const string &b) {
M = a.length();
N = b.length();
if (M < N) {
A = a;
B = b;
} else {
A = b;
B = a;
swap(M, N);
}
}
int editDistance () const {
const int offset = M + 1;
const int delta = N - M;
const int size = M + N + 3;
int fp[size];
for (int i=0;i<size;++i) fp[i] = -1;
int p = -1;
do {
++p;
for (int k=-p;k<=delta-1;++k) {
fp[k+offset] = snake(k, max(fp[k-1+offset]+1, fp[k+1+offset]));
}
for (int k=delta+p;k>=delta+1;--k) {
fp[k+offset] = snake(k, max(fp[k-1+offset]+1, fp[k+1+offset]));
}
fp[delta+offset] = snake(delta, max(fp[delta-1+offset]+1, fp[delta+1+offset]));
} while (fp[delta+offset] != N);
return delta + 2 * p;
}
private :
int snake (int k, int y) const {
int x = y - k;
while (x < M && y < N && A[x] == B[y]) {
++x;
++y;
}
return y;
}
string A;
string B;
int M;
int N;
};
int main(int argc, char *argv[]){
if (argc < 3) {
cerr << "few augument" << endl;
return -1;
}
string A(argv[1]);
string B(argv[2]);
Diff d(A, B);
int editDistance = d.editDistance();
cout << "editDistance: " << editDistance << endl;
return 0;
}
Wuのアルゴリズムでは2つの要素列をA、B、それぞれの長さをM、NとするとN≧Mなので、①のコンストラクタではN≧Mの関係がつねに成り立つようにします。
②のeditdistance関数がエディットグラフを探索するメインロジックになります。変数fpが各対角線上で到達可能な最遠点のy座標を格納する配列になりますが、探索範囲が-p≦k≦Δ+pなので、そのままだと配列fpの添字が負の値になる場合があるため、添字が負の値にならないように調整する必要があります。
pの最大値がM、またfp(k,p)を計算するにはfp(k-1,p')とfp(k-1,p'')が必要であることを考慮すると、配列fpの添字が負の値にならないためにはM+1個分配列の位置をずらせば良いことになります。
また、配列fpのサイズは同様にPの最大値がM,探索範囲が-p≦k≦Δ+pなので、k=Δ+P=Nの際に配列fpの添字の値がk+1+offset=N+1+M+1=M+N+2で最大になるため、配列fpのサイズは(配列の添字が0から始まることを考慮して)M+N+3になります。そしてp=0からループを回していってfp(k,p)=Nとなったときのpの値(SESにおける削除の合計数)をもとに編集距離を計算します。
③のsnake関数の仕事はfp(k,p)から対角線上に進んで到達できる最大のy座標を返すことです。各要素列の現在位置の要素を1つづつ比較して同一であればそれぞれの要素列の位置を+1進めて、最終的にy座標を返します。また、x座標はk=y-xにより、x=k-yで求めることができます。
Wuのアルゴリズムの問題点
Wuのアルゴリズムは2つの要素列が似通っている場合、非常に高速に動作しますが、そうでない場合は探索する範囲が広くなった分遅くなり、SESを求めるために記録する経路のサイズも大きくなります。今回のように比較対象となる要素列が短い文字列であればとくに問題ではないのですが、万単位の行からなるファイル同士を比較したりするとなると、実装によっては実用上使い物にならないくらい遅くなったり、メモリを大量に消費するようになってしまう可能性があるので、工夫が必要になります注9。
その他のアルゴリズム
本稿ではWuのアルゴリズムについて解説しましたが、ここでは他のアルゴリズムについて軽く紹介します。
動的計画法(Dynamic Programming)
動的計画法(以下、DP)とはひとつひとつの小さな問題の解を組み合わせて、より大きな問題を解くというもので、diffに限らずいろいろな応用ができるアルゴリズムです。DPを使った差分の計算における小さな問題の解とは、2つの要素列の先頭からの各部分列におけるLCSの長さです。各部分列のLCSの長さは各一要素分前の部分列のLCSの長さがわかっていれば計算することができるので、先頭からの各部分列のLCSの長さを全部求めていけば最終的にもとの2つの要素列のLCSの長さが求められます。
また、各部分列のLCSの長さを求める過程で、どの部分列を選択したかという情報も保存します。
最後にこの情報を逆順にたどっていけば、編集距離、LCS、SESを求めることができます。
DPを使った差分の計算では単純に各部分列のLCSの長さを保存しようとすると、M×N(M, Nはそれぞれの要素列の長さ)の表が必要になるので計算量がO(MN)、計算に必要なメモリもM×Nになります。
Myersのアルゴリズム
MyersのアルゴリズムはWuのアルゴリズムと同じく、差分の計算問題をエディットグラフ上の最短経路問題に還元するアルゴリズムです。Dは編集距離を表しており、Wuのアルゴリズムと同じような感じで探索範囲を-D<=k<=Dに絞り込むことによって、計算効率を向上させています。
GNU diffutilsや分散型バージョン管理システムの1つであるGitのdiffエンジンとして採用されているXLibdiffの実装はこのアルゴリズムを基にしています[10]。
Gestalt Approach
Gestalt ApproachはWuのアルゴリズムやMyersのアルゴリズムと違い、差分の計算問題をエディットグラフ上の最短経路問題に還元するのではありません。2つの要素列中の連続する共通部分を探し出し、その共通部分を中心に2つの要素列をそれぞれ分割します。そして、その分割した2つの要素列の左部分と右部分のそれぞれから再び共通部分を探し出すといったことを繰り返し、最後にその共通部分を全部つなげてLCSなどを算出するというアルゴリズムです。
最後に
本稿のサンプルコードでは、編集距離を求めるところまでしか紹介できませんでしたが、興味のある方は本稿でも紹介した拙作のdtlやGNU diffutilsまた各種バージョン管理システムのソースコードに含まれているdiffエンジンのソースコードを読んでみると良いでしょう。また、githubに筆者が各種言語でWuのアルゴリズムを利用して実装した差分計算プログラムのソースコードがあります。
- 参考文献・URL
- E.W.MYERS, "An O(ND) Difference Algorithm and Its Variations"
- Sun Wu, Udi Manber, G.Myers, W.Miller, "An O(NP) Sequence Comparison Algorithm"
- 『アルゴリズムイントロダクション「第2巻」アルゴリズムの設計と解析手法 改訂2版』
T.コルメン、C.ライザーソン、R.リベスト、C.シュタイン共著/浅野哲夫、岩野和生、梅尾博司、山下雅史、和田幸一共訳/近代科学社/ 987-4-7649-0335-7
- 『近似アルゴリズム』V.V.ヴァジラーニ著/浅野孝夫訳/シュプリンガー・ジャパン/987-4-4317-00991-6
- PATTERN MATCHING:THE GESTALT APPROACH
URL:http://www.ddj.com/184407970?pgno=5
- 文書比較アルゴリズム
URL:http://hp.vector.co.jp/authors/VA007799/viviProg/doc5.htm
- Webサイト「/0」内の記事――diff(1)、diff(2)、diff(3),
URL:http://www.slash-zero.jp/archives/program/466
URL:http://www.slash-zero.jp/archives/program/468
URL:http://www.slash-zero.jp/archives/program/476
- 各種言語(C, Go, Java, Lua, Perl, Python, Ruby)によるWuのアルゴリズムの実装
URL:https://github.com/cubicdaiya/onp











