以前gihyo.jpの特集で、Nゲージのエディタを取り上げたことがあります。このエディタでは、レールをドラッグ操作で動かせるようにしました。

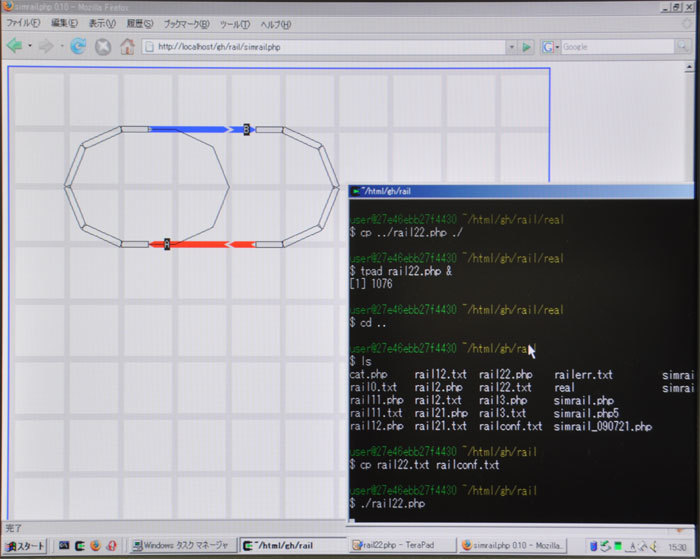
レールの始点または終点から、x, y共に±3以内だったら端点と見なすことで、端点をドラッグすると変形になる処理が実現できます。これは簡単ですね。ifの条件で書くと

((sx - 4 < x)&&(x < sx + 4)&&(sy - 4 < y)&&(y < sy + 4))

のようになります。

では、レールの上をドラッグしたら移動になる、という処理はどう書けばよいでしょうか。レールは直線ですが、水平や垂直ではなく斜めにもなります。もちろん、1ドット幅を正確にクリックしないといけないのでは実用になりませんから、ある程度の幅を持たせる必要があります。高校で「点と直線の距離」を習った記憶がありますが、ルートが出てくるなど計算が複雑なため、たくさんの線があると計算に時間がかかるかも知れません。

実は、「⁠ベクトルの外積」というものを使うと、簡単に実現できます。名前は大げさですが、とても簡単ですので、ぜひこの機会に知っておいてください。

外積を使ってみよう

結論から言うと、ベクトルの外積とは四角形の面積をとても簡単に計算する方法です。まずは次のスクリプトを実行して、ベクトル（矢印）の頭をマウスでドラッグしてみてください。

• サンプルスクリプト（crossproduct.html）

四角形の中に面積が表示されています。

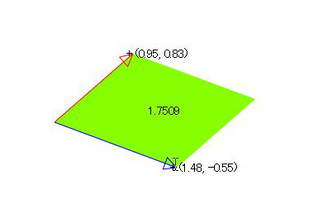
この面積は、実は

(x0 * y1 - x1 * y0)

というシンプル極まりない計算で求めることができます。補助線を引いて三角形に分割すると、直観的に理解できるのですが、ここではこうやって計算できるのだと理解していただければ十分です。しかも、矢印の左右が逆転すると、外積がマイナスになります。このスクリプトでは、プラスとマイナスで色が変わるようにしてあります。

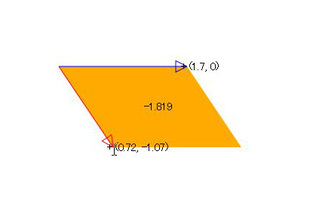
では、これをどう使えばいいのでしょうか。今度はこちらのスクリプトを実行してみてください。

• サンプルスクリプト（crossproduct2.html）

四角形の4つの辺が矢印になっており、マウスを動かすと色が変わります。この色は、その矢印と、マウスに向かう矢印（表示されません）との外積のプラスマイナスを表わしています。矢印の矢の向きから見て左側にマウスカーソルがあるときは青に、右側にマウスカーソルがあるときは赤になるのを確認してください。

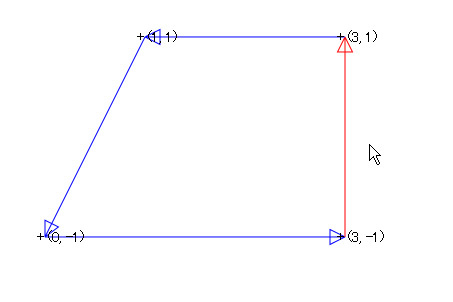
では、四角形の内部にマウスカーソルを持ってくると、どうなるでしょう。すべて同じ色になりますね。最初の状態では全部青になりますが、座標をドラッグして対角を入れ替えると（矢印の向きが右まわりになるようにすると⁠）⁠、全部赤になります。例外として「く」の字をした、いわゆる凹多角形の場合はうまくいきませんが、凸多角形の場合は必ずこうなります。

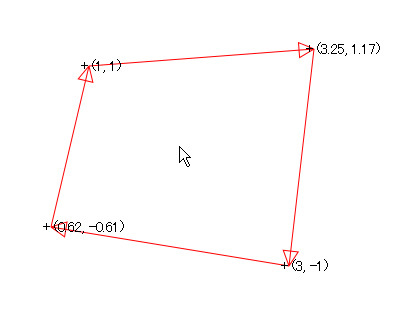
つまり、ドラッグしたいレールについては、ドラッグを受け付ける範囲を多角形で表わしておきます。マウスがプレスされたら、それぞれの外積を計算して、多角形のすべての外積が同じ符号であれば、その多角形の内部にあるとわかります。JavaScriptではあまり問題になりませんが、組込みシステムの場合は除算に時間がかかることがあるため、乗算と加減算だけで計算できる外積が有利というのもあります。

線が交差したらエラーにしたいときは

外積のもう1つの使い方を紹介しましょう。2つの線が交わるかどうかを知りたいときがあります。たとえば、マウスで引いた線と交わる図形をすべて見つけるにはどうしたらいいでしょうか。

具体的には、ABという線と、CDという線を考えます。この2つの線が交差しているか、それとも離れているのかは、どうしたらわかるでしょうか。

これも、外積のプラスマイナスを使います。線ABから見て、左側の点の外積はプラスに、右側の点の外積はマイナスになるとしましょう。すると、もし点Cの外積がプラスで、点Dの外積もプラスだとしたら、両方とも線ABの左側にあることになります。これでは、どうがんばっても線ABと線CDは交差することができません。線ABの左側に点Cがあり、反対側に点Dがある、あるいはその逆でないと、交点はできません。つまり、プラスマイナスが逆になっていることをチェックする必要があります(これは、乗算の結果がマイナスになることをチェックすればokです)。

そして大事な点ですが、線CDから見て点Aと点Bが反対側にあることも確認します。これらがすべてokなら、線ABと線CDは交差していることがわかります。

外積はとてもシンプルで、応用が利きます。すぐに使うことはないかも知れませんが、座標計算のときはぜひ思い出してください。