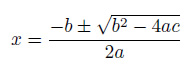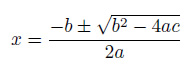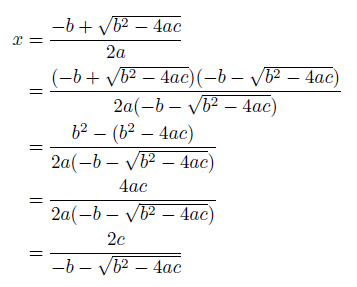前回は浮動小数点数のエラー・誤差のうち、「オーバーフロー/アンダーフロー」と「桁落ち」について学びました。今回は演習として、「桁落ち」とその回避方法を経験してみましょう。
問題:二次方程式の解の公式で、桁落ちを生じないように式変形しましょう。
解の公式
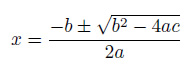
(1)a=0.25,b=20,c=0.1 の場合、float型で計算するとどの程度桁落ちを発生するでしょうか。プログラムを作成して実行してみましょう。
(2) 式変形を行い、桁落ちを生じない形の式を導きましょう。
(3) 式変形後の式をプログラムに追加して再計算し、桁落ちが改善されているか確認しましょう。
解説
問題:二次方程式の解の公式で、桁落ちを生じないように式変形しましょう。
(1)a=0.25,b=20,c=0.1 の場合、どの程度桁落ちを発生するでしょうか。プログラムを作成して実行してみましょう。
1:
2:
3:
4:
5:
6:
7:
8:
9:
10:
11:
12:
13:
14:
15:
16:
17:
18:
19:
|
//filename : Ketaochi.java
import java.io.*;
class Ketaochi {
public static void main(String[] args)
throws IOException {
float a = 0.25f;
float b = 20f;
float c = 0.1f;
float x1 = 0f;
float x2 = 0f;
x1 = ( -b + (float) Math.sqrt(b*b-4*a*c) ) / (2 * a) ;
x2 = ( -b - (float) Math.sqrt(b*b-4*a*c) ) / (2 * a) ;
System.out.println("x1 = " + x1);
System.out.println("x2 = " + x2);
}// end of main
}// end of class
|
|---|
平方根の計算結果をfloat 型にキャストしているのは、Math.sqrt メソッドの返り値がdouble 型であるためです。そのまま計算結果をfloat 型の変数に代入しようとすると精度の低下を警告するエラーを発してコンパイルを終了させてくれません。
このプログラムの実行結果は次の通りです。
Ketaochi.java の実行結果
x1 = -0.005001068
x2 = -79.994995
正確なx1 の値は.0.005000312539 ・・・ なので、プログラムの実行結果は3桁の有効数字しかありません。x2 の正確な値は.79.9949968 ・・・ なので、かなり正確な計算結果です。
(2)式変形を行い、桁落ちを生じない形の式を導きましょう。
問題となる式は、分子が負の値との加算の場合であるので、これを負の値との減算の形に変形しましょう。
さあ、これで近接する値の減算に相当する分子部分がなくなりました。導いた式の分母は、負の値から正の値を減算しますから、絶対値が大きくなる計算に改善され、桁落ちが回避できるはずです。
(3)式変形後の式をプログラムに追加して再計算し、桁落ちが改善されているか確認しましょう。
1:
2:
3:
4:
5:
6:
7:
8:
9:
10:
11:
12:
13:
14:
15:
16:
17:
18:
19:
20:
21:
22:
|
//filename : Ketaochi2.java
import java.io.*;
class Ketaochi2 {
public static void main(String[] args)
throws IOException {
float a = 0.25f;
float b = 20f;
float c = 0.1f;
float x1 = 0f;
float x2 = 0f;
float x3 = 0f;
x1 =( -b + (float) Math.sqrt(b*b-4*a*c) ) / (2 * a) ;
x2 =( -b - (float) Math.sqrt(b*b-4*a*c) ) / (2 * a) ;
x3 = (2 * c) / ( -b - (float) Math.sqrt(b*b-4*a*c) ) ;
System.out.println("x1 = " + x1);
System.out.println("x2 = " + x2);
System.out.println("x3 = " + x3);
}// end of main
}// end of class
|
|---|
このプログラムを実行した結果は次の通りです。
Ketaochi2.java の実行結果
x1 = -0.005001068
x2 = -79.994995
x3 = -0.005000313
先ほどの結果と比較すると、丸めの影響を考えると7 桁目まで正しい値と一致し、有効数字が大幅に改善していることがわかります。
実際の数値計算においては、実行時までa,b,c の値がわからないことがあります。そのような場合には、a,b,c の値に応じて解の公式を切り替えるプログラムにする必要があります。
コンピュータは計算機械ですから、解の公式くらい精度良く計算できるものと思いたいのですが、実はそうでもないのだ、ということが今回よくわかっていただけたでしょうか。