機械や建築物をつくるためには必ず図面がつくられます。特に複数の人間で物作りをする場合には図面が欠かせません。お互いに正確な情報の交換・共有を行うために必要だからです。これは、言葉で表すのとは別の意味で図面がものごとを明確に表現できるからです。ですから、図面は一人で物作りを行う場合にも力を発揮します。図面にすることで不明確であった部分が明らかになります。図にするためには未確定である部分もある程度確定しなければなりません。図面はそれまで気がついていなかった部分を教えてくれたり、すっきり納得させてくれたりします。
論理の数学で用いる図にも同じ効果があります。今回は「論理を視覚的に表現するための図法」であるベン図を学びましょう。
図22.1 図面で作るものを明らかにする

ベン図
ベン図は、ある命題が真になる場合と偽になる場合を、ひとつの円形、あるいは交差する複数の円形を用いて表現する方法です。円の中は命題が真の場合をあらわします。円の外は偽の場合です。
高等学校ではこのベン図を用いて簡単な集合論を学習します。論理も真である事柄の集合と、偽である事柄の集合であると考えれば、集合論の図が論理でそのまま用いられることが不思議でないとわかるでしょう[1]。
図22.2 論理変数がひとつの場合
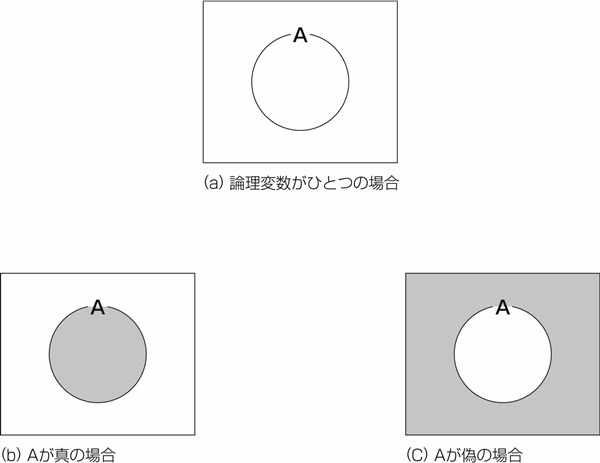
図22.2の(a)に最もシンプルなベン図を示します。図中の四角形の内部は、考え得る全ての場合を表します。
図中の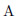 という名前で囲まれた部分が、論理変数[2]
という名前で囲まれた部分が、論理変数[2]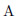 が真である(成り立つ)範囲を表してます。これは論理式
が真である(成り立つ)範囲を表してます。これは論理式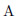 =1の場合をあらわす範囲で、単に
=1の場合をあらわす範囲で、単に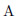 と書きます。この範囲
と書きます。この範囲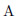 を図中で明示する場合にはハッチング(斜線)を施し、図22.2の(b)のようにします。
を図中で明示する場合にはハッチング(斜線)を施し、図22.2の(b)のようにします。
範囲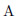 の外の部分は論理変数
の外の部分は論理変数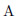 が偽である(成り立たない)範囲を表します。論理式
が偽である(成り立たない)範囲を表します。論理式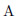 =0をあらわす範囲で、
=0をあらわす範囲で、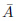 (「エーバー」と読む)と書きます。この範囲
(「エーバー」と読む)と書きます。この範囲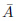 を図中で明示する場合には、図22.2の(c)のようにします。
を図中で明示する場合には、図22.2の(c)のようにします。
直感的で大変分かりやすいですね。
図22.3 論理変数がふたつの場合
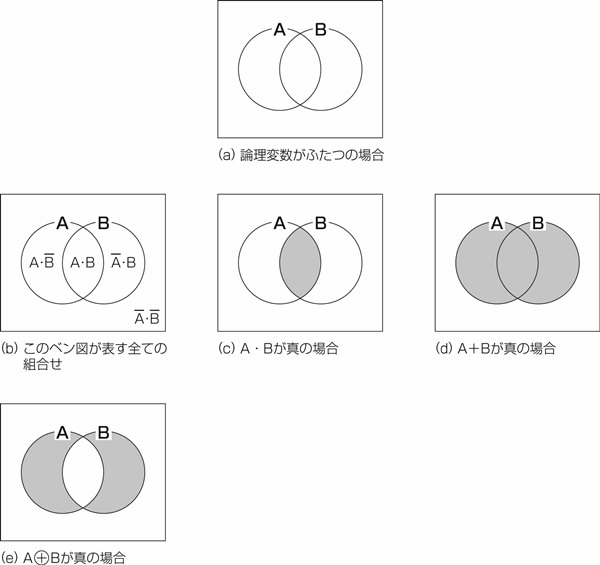
図22.3の(a)は論理変数がふたつの場合のベン図です。2つの円は必ず交差させて描きます。そうすることで2つの論理変数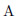 ,
,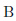 がとり得る全ての場合(4つ)を表現できるからです。
がとり得る全ての場合(4つ)を表現できるからです。
図22.3の(b)をみると、全ての場合が網羅されていることがわかるでしょう。このベン図で、論理変数が2つの場合の全ての論理式の真偽を表現できます。例えば(c)は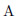 ・
・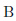 が真の場合、(d)は
が真の場合、(d)は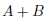 が真の場合、(e)は
が真の場合、(e)は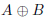 が真の場合です。その他どんなものも(a)を塗り分けることで表現可能です。例えばド・モルガンの法則をベン図で表すと図22.4のようになります。
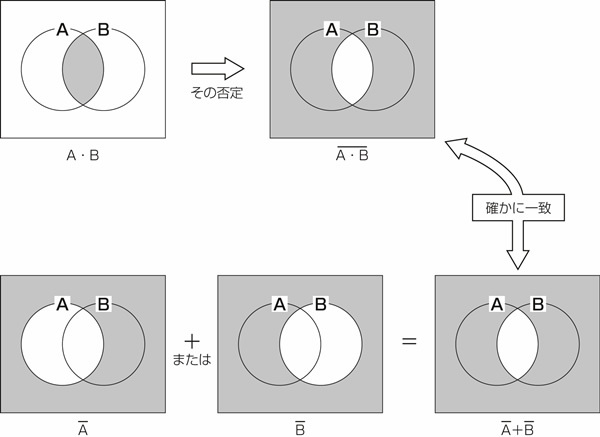
が真の場合です。その他どんなものも(a)を塗り分けることで表現可能です。例えばド・モルガンの法則をベン図で表すと図22.4のようになります。
図22.4 ド・モルガンの法則をベン図で
今回はここまで
ベン図の優れているのは、図を塗り分けることで論理の状態を視覚的にとらえられることです。文章や式で理解するのが苦手でも、図にすると納得、という方もおられることでしょう。ベン図の便利さは実際に手を動かして描いてみることで初めて実感できます。次回は論理式をベン図で示す問題に取り組みましょう。


![]() という名前で囲まれた部分が、
という名前で囲まれた部分が、![]() が真である
が真である![]() =1の場合をあらわす範囲で、
=1の場合をあらわす範囲で、![]() と書きます。この範囲
と書きます。この範囲![]() を図中で明示する場合にはハッチング
を図中で明示する場合にはハッチング![]() の外の部分は論理変数
の外の部分は論理変数![]() が偽である
が偽である![]() =0をあらわす範囲で、
=0をあらわす範囲で、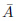
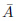 を図中で明示する場合には、
を図中で明示する場合には、
![]() ,
,![]() がとり得る全ての場合
がとり得る全ての場合![]() ・
・![]() が真の場合、
が真の場合、![]() が真の場合、
が真の場合、![]() が真の場合です。その他どんなものも
が真の場合です。その他どんなものも



