今回はペンと紙を一枚ご用意下さい。問題に示す論理式を紙の上にベン図として描き表しましょう。その際、左辺は左辺だけで、右辺は右辺だけでベン図を考えましょう。代数的に左辺を変形して右辺の形に持って行ってからベン図を描くのが今回の目的ではありません。四角形の中に、式中に登場する論理変数の数だけ丸を描き、真のところにハッチング(斜線)を施していくのです。
この作業をすることで、無味乾燥に思えた論理式がすっきり納得できることでしょう。
問題:以下に示す論理式を、ベン図を使って視覚的に示しましょう。
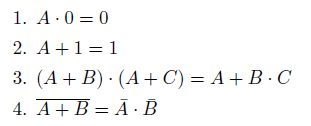
解説
1.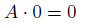
図23.1 論理式をベン図で示す1.
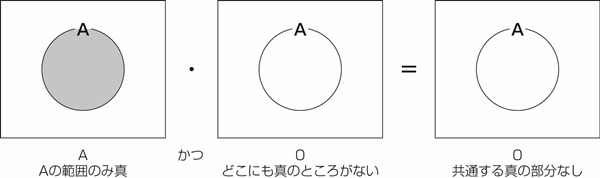
図23.1は問題の論理式をベン図で表現したものです。左辺からみていきましょう。
Aは論理変数Aが真である場合を示します。ベン図ではAの示す範囲にハッチングを施します。
次に0である部分を図中に明示します。真であるところにハッチングを施すのですが、0(常に偽)であるということは、どこにも真のハッチングが施された部分があらわれません。ですから、ベン図は真っ白です。
この2つのベン図の論理積をとるということは、2つのベン図で共通して真である部分(ハッチングの施された部分)を探せばよいのです。ところが、片方が常に0ですからハッチングの施された共通の部分はありません。
以上のことから、左辺の演算結果を表す右辺のベン図は0、すなわち真っ白なのです。
2.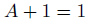
図23.2 論理式をベン図で示す2.
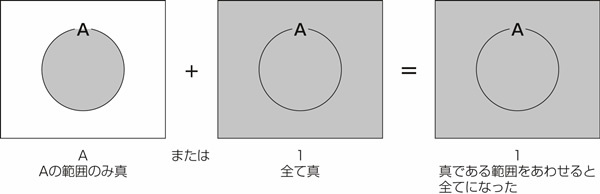
図23.2は問題の論理式をベン図で表現したものです。左辺からみていきましょう。
問題1.と同様に、Aは論理変数Aが真である場合を示します。
次に1である場合のベン図を作成します。常に1なのですから、Aの中も外も真です。全体にハッチングを施します。
以上2つのベン図の論理和をとると言うことは、2つのベン図で真のところを全て選び出せばよいのです。選ぶと言っても、1のベン図は全面真ですから、左辺の演算結果を表す右辺のベン図は1、すなわち全面が真、全面ハッチングを施した状態になります。
3.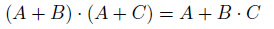
図23.3 論理式をベン図で示す3.
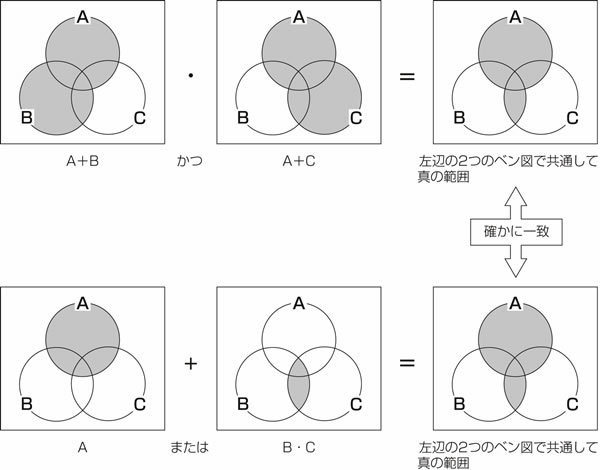
図23.3は問題の論理式をベン図で表現したものです。左辺からみていきましょう。左辺を図中上側に示しています。問題1.、2.の手順と同様にベン図を追ってみてください。すると、最終的に右上のベン図が出来上がることが納得できるでしょう。
次に図中の下側に右辺を示します。これも同様に左から右にベン図を追っていくと、右下のベン図が納得できるはずです。
するとどうでしょう、最終的に右端上下に並んだ図が一致していることがわかります。それぞれの示す論理式の形は異なりますが、ベン図がそれぞれの論理式の等価なことを教えてくれるわけです。面白いですね。
4.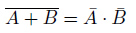
図23.4 論理式をベン図で示す4.
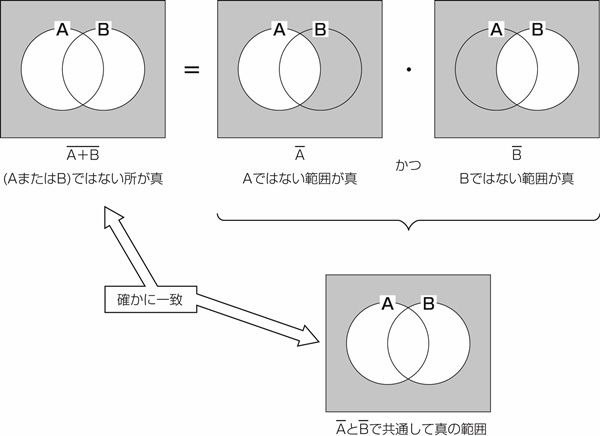
図23.4は問題の式をベン図で表しています。これはド・モルガンの法則の式です。
左辺はA+Bではない部分、すなわち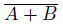 が真の部分にハッチングを施したベン図です。
が真の部分にハッチングを施したベン図です。
右辺は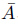 、
、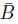 のベン図です。これらの論理積をとると、図中下側のベン図が得られます。
のベン図です。これらの論理積をとると、図中下側のベン図が得られます。
左辺と右辺のベン図が一致していますね。
不思議な魔法に思えるド・モルガンの法則ですが、ベン図で表してみると不思議と納得してしまいます。ベン図とは全く便利な方法ですね。
ベン図を描くと、抽象的だった論理式がなんだかすっきりと図示されて「確かに、確かに」と納得できると思います。問題で示した式の左辺と右辺の論理的な意味が変わっていないことがわかります。ベン図の有効性がお分かりいただけたと思います。
プログラムを作っていてif文が絡み合ってわけがわからなくなったら、ベン図を書いて場合を列挙して検討してみるといいことがあるかもしれません。真理値表でも同じことが期待できますが、図には図の良いところがあるものです。困ったときにはいろんな方法を試してみましょう。
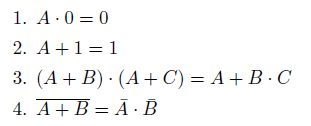
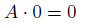

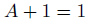

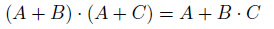

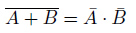

![]() が真の部分にハッチングを施したベン図です。
が真の部分にハッチングを施したベン図です。![]() 、
、![]() のベン図です。これらの論理積をとると、
のベン図です。これらの論理積をとると、


