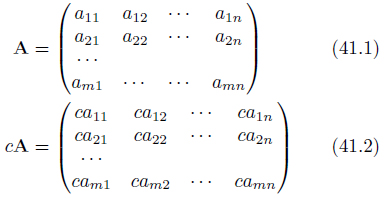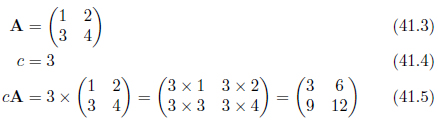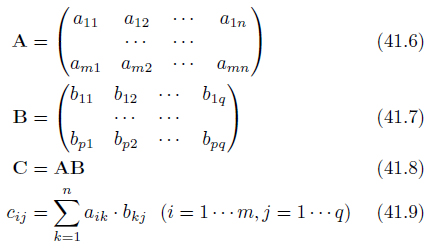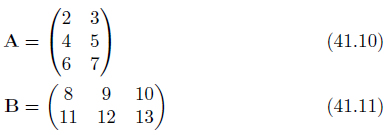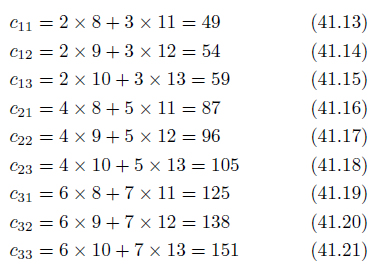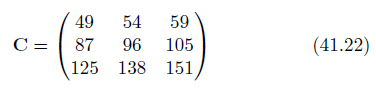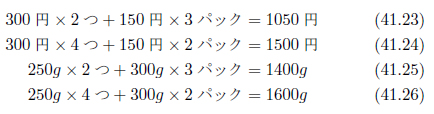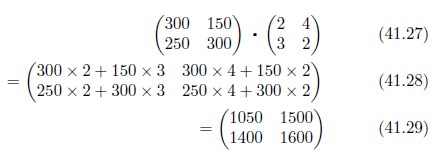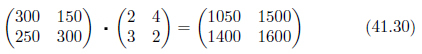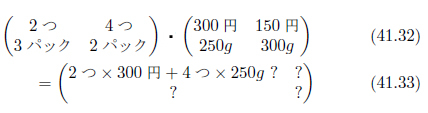柔道で新しい技を学ぶとき、先ずは練習相手と約束をします。
- 技を掛ける方(取り)は無理な力を使わないこと。
- 技を掛けられる方(受け)は抵抗をしないこと。
この約束の下で稽古することで、双方が技の形に集中できます。取りは無理な力を使うと形が崩れます。これでは、いざ本番で技を掛けようとしても力んでしまって技になりません。受けの方も、稽古の時に力んでいると、技の本質を知ることが出来ません。ですから、試合で相手が技を出してきても、それと察知することが出来ません。力んで稽古することは、お互いに不利益なのです。
さて、数学的な法則やプログラムのアルゴリズムを学習するときにも同じ理屈を適用できます。新しいことを学ぶときには、無理に力んで理解しようとしても、なかなか身に付きません。身に付かないばかりか、本質を見過ごしてしまって肝心のポイントを落としてしまいがちです。ある法則やアルゴリズムが複雑だと感じられるときには、シンプルな具体例を適用してみましょう。楽に処理出来たと感じたら、次のステップへ。具体例では煩雑になりすぎて、これは一般化した方が良いのでは?と感じたとき、そのときこそ、一般化した法則やアルゴリズムに取り組む頃合いかもしれません。
図41.1 力を抜いて、無理なく

行列のスカラ倍
行列のスカラ倍とは、行列に含まれる成分を全てスカラ倍することです(式41.2)。
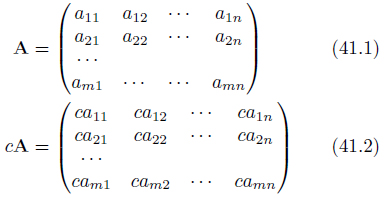
具体的な数値をあてはめて、計算した例を示します。
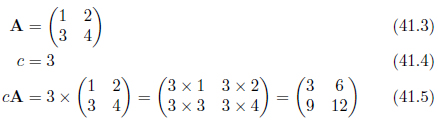
式41.2を見ると、行列のスカラ倍の記法の便利さが感じられます。
行列のスカラ倍には、ベクトルのスカラ倍と同じように、交換法則や結合法則が成り立ちます。
行列の乗算
行列の乗算の一般式
行列同士の乗算は次の手順で実行します。
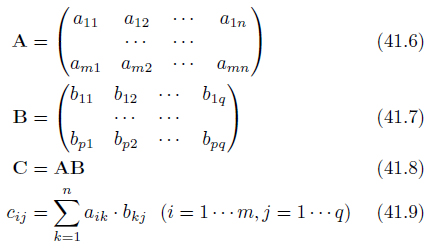
ただし、乗算はAの列数nとBの行数pが等しいときのみ可能です。式41.9は乗算結果となる行列Cの(i行目,j列目)成分の値です。
計算結果の行列Cは、行数が行列Aの行数m、列数が行列Bの列数qとなります。
式41.9中のiとjは、よくプログラム中でカウンタとして用いるアルファベットです。このため、式41.9の操作中に値が変化するものと思いこみやすいのですが、変化するのはkだけです。式41.9は、とてもシンプルな式なのです。「Aについては横移動、Bについては縦移動」と読んでください。
行列の乗算の例
行列の乗算を一般的に表すと、式41.9のようにシンプルに表現できるのですが、慣れないうちは、どんな計算なのか具体的にイメージしにくいものです。そこで、小さな行列同士の乗算をしてみましょう。自分の手で具体的な計算手順を追えば、一般式の意味が納得できると思います。
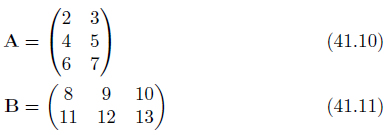
行列Aは2列、行列Bが2行ですから、乗算が可能です。

行列Cの成分は次の通り。
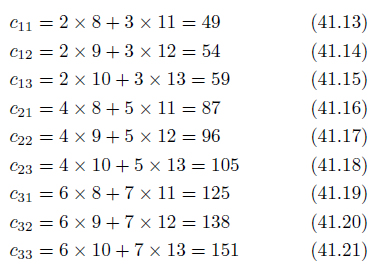
以上の計算の結果、求める行列Cは次のようになります。
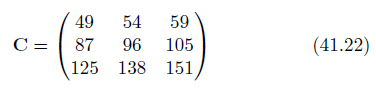
行列Cの行数はAの行数3、列数がBの列数3となっています。計算のイメージはつかめたでしょうか。
行列の乗算の具体例
行列の乗算を活用する具体的なシーンを想像してみましょう。
例えば、こんな具合です。
「今日はチーズと卵の特売日。私は自分と実家の両親の分の買い物に出かけました。チーズはひとつ300円で250gです。卵はひとパック150円で300gです。私はチーズを2つ、卵を3パック。実家のためにチーズを4つ、卵を2パック買いました。自分の出費と実家のための立て替え分はいくらになるでしょう。私の持ち物の重さと、実家のためのものの重さはいくらになるでしょう。」
これは次のような式になります。
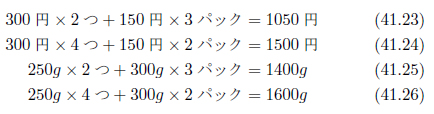
行列を用いると、次のようになります。
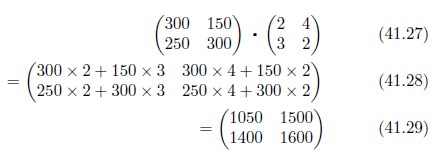
いかがですか?通常の等式と、行列を用いた式の見事な対応を感じることが出来ましたか?意味はまた別の時にゆっくり考えるとして、ぱっと見て、これら二つの場合のどちらがシンプルでエレガントでしょう。「円」とか「パック」が行列の場合に無いのを差し引いても、行列で表した式には加算の+が表れません。式41.28を省けば、次のようになり、ぐっと魅力的になります。表41.1に、行列の式が表している計算の具体的内容を記入してみました。行列の計算が、左辺から右辺へどのように変容しているかを見ると、更に行列の式の働きがわかりやすいでしょう。
表41.1 式41.30の意図をわかりやすくしたもの

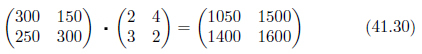
今回は、自分と実家の買い物の話でしたが、これが町内会の鍋会の買い出しだったら、ネギに鶏肉に豆腐にみそに・・・ぞっとしませんか?行列で書き表せば、手で書くにしてもずいぶん無駄なく出来そうですよ。
行列の乗算に交換法則は成り立たない
行列の乗算には交換法則が成り立ちません[1]。

論より証拠、実際に先ほどの計算例の行列を前後交換して計算してみてください。結果はどうなるでしょうか?
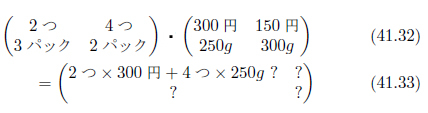
金額と重さの合計なんて、計算が全く意味をなしていませんね。行列の式を取り扱うとき、交換法則が成り立たないことをしっかりおさえておかなければなりません。
問題:行列の乗算を行うメソッドを作りましょう。
整数を成分として持つ行列の乗算メソッドを、配列を用いて作ってください。
メソッドはサンプルコードに示すようにvMultiMatrix(A,B,C,i,j,k,l)のように呼び出しましょう[2]。行列Aと行列Bの積を行列Cに格納してください。引数の意味についてはソースコードをご覧下さい。
問題を簡単にするために、乗算メソッドで引数の次元数をチェックしなくて結構です。代わりに、メソッドを呼ぶ際に、与えた行列の次元を渡します。これで、ずいぶん簡単になったはずです。
コードを組む前に、一度小さな行列を手で計算し、そのステップを紙の上で確認してみましょう。自分が今、どの行列の何行目・何列目を計算しているのかをしっかりととらえましょう。それが出来たら、コードに置き換えるのです。
ソースコード:HairetsuDeMatrixMultiplication.java
//サンプルコード
//行列の積をとる。配列版。
//filename : HairetsuDeMatrixMultiplication.java
class HairetsuDeMatrixMultiplication {
public static void main(String[] args) {
int a[][] = //行列A 2x3
{ { 3,4,5 },
{ 6,7,8 } };
int b[][] = //行列B 3x2
{ { 9,10 },
{ 11,12 },
{ 13,14 } };
int c[][] = new int[2][2]; //行列C
//C = A x B
vMultiMatrix(a,b,c,2,3,3,2);
//結果表示
for( int Rc = 0 ; Rc
解説
式41.9をいきなりコードに置き換えようとしても、どこから手をつけて良いのか困ってしまったことでしょう。ところが、紙と鉛筆の上で解いた手順を確認しながらコードに置き換えてみると、不思議と簡単にコーディング作業出来てしまうものです。アルゴリズムを紙の上で追いかけることは、思考を助けるためにとても有効なのです。
ソースコード:HairetsuDeMatrixMultiplication.java の不足部分
static void vMultiMatrix(int a[][], int b[][], int c[][],
int i, int j, int k, int l){
for( int Rc=0; Rc
今回はここまで
今回は行列のスカラ倍と行列の乗算について学びました。行列の乗算では、「可換でない」という新しい概念を学びました。式をシンプルに記述するために考えられた行列ですが、乗算では可換でないという足かせもあるわけです。確かに重い足かせですが、これをうまく回避したり、足かせを受けてあまりあるメリットがあるわけですから、へこたれることなく学び続けましょう。