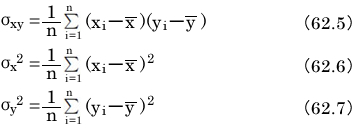「大風がふけば桶屋がもうかる」とか「バタフライ効果」だとか、物事・出来事は関連を持って存在するものだと考えられています。ただ、それらの関連を明確に表現する方法が無いために、カンや推測で判断せざるを得ないことが多いですね。

スポーツの世界でも、真剣な勝負であるほど、ある攻撃を仕掛けたときに相手がどのような反応を示すか、というデータを集めて分析し、次の試合に備えます。あるプレーに対して、相手がどう対応する傾向が強いか、それを知ることが出来ればこんな有利なことはありません。もちろん、スポーツには即応性が要求されますから、最後の瞬間は本能に頼るのですが。しかし、データのバックアップがあるのと無いのとでは、大きな違いです。

今回学習する内容は、一対一に対応するデータの集合について、線形な関係があるかどうかを数値で評価する方法についてです。数値化することで比較が可能になります。統計の数学の学習の終わりにぴったりな内容です。

相関係数とは

あるデータの集合について、そのデータによく当てはまる直線（回帰直線）の式を最小二乗法で決めました。さて、その直線の式はどの程度データに当てはまっているのでしょうか。「⁠よく当てはまっている」「⁠あまり当てはまっていない」と、言葉で表現しても、具体性がありません。そこで、当てはまり具合を数値で表現できると便利です。

それはつまり、「⁠データが予想どおりか、数量的に表す」ということです。これは便利です。

相関係数[1]は、求めた回帰直線の式がどれだけ元のデータに当てはまっているかを-1から1の間の値で表現したものです。絶対値が1に近いほどデータは回帰直線の周辺に密集しています。0に近いほどバラバラに広く分布します。

また、相関係数が正の値なら、データの集合に右上がりの比例関係があります（正の相関⁠）⁠。負の値なら右下がり（負の相関⁠）⁠。0ならばデータに比例関係が無いことを表します（無相関⁠）⁠。

厳密には、相関係数は、データが直線に当てはまっているかどうか、というニュアンスではなく、データが直線にそってばらついていると仮定して、そのばらつき具合の大小を数値で表したものです。ですから、相関係数の値が0であるということは、データをグラフ用紙にプロットしたとき、まるで雨粒が降り注いだようにバラバラに位置しています。相関係数の絶対値が1であれば、全てのデータが一直線上にぴしっと並んでいることを表しています。

また、相関係数の正負がグラフの傾きを表しているからといって、相関係数の絶対値の大小が直線の傾きの緩急を表現しているのではありません。

相関係数

先ずは大雑把に、相関係数がどのように組み立てられているものなのかを示します。

回帰直線がよく当てはまっているかどうかは、次の式で定義する誤差dの値の大小で判定できます。

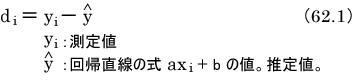
しかし、誤差は測定値や推定値のオーダー（桁）が大きければ、誤差の割合が小さくとも、数字として大きくなります。他の場合との比較には向きません。そこで、次の式を導きます（導出の手順を省きます⁠）⁠。

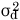が小さければ、回帰直線がよく当てはまっているといえます。測定値と推定値の分散の値が近くなるからです。よって、次の式の値が大きくなれば回帰直線がよくあてはまっているといえます。

式62.3の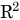を決定係数[2]といいます。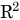=1ならば、誤差はゼロで完全に予測値が測定値と一致しています。このときを完全相関[3]といいます。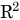=0のときを無相関[4]といいます。

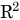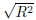決定係数の平方根=rを相関係数[5]といいます。ようやく相関係数にたどり着きました。

式62.3を変形して、次の式で相関係数を得ることが出来ます。

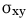はxとyの共分散[6]といいます。式62.4の各値は、以下の式で求めます。

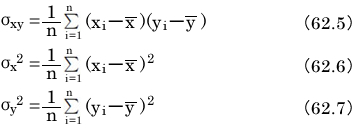
さて、今回はこれらの式がどのように導かれたか、ということは後回し、問題から先に取り組みましょう。式の導出の手順については、次回じっくり取り組むこととします。

問題　CSVファイルのデータから、紙と鉛筆、電卓を用いて、相関係数を計算しましょう。

データファイルdata001.csvには3つの座標値しかありませんから、相関係数を手で計算するのは大した手間ではありません。手計算でおおよその値を得て、次回の問題のプログラムが正しく実行されたかどうかを確かめるための準備をしておきましょう。

解説

以下に計算の様子を示します。切りの悪い数字はなるべくきりの良い数字に丸めて概算します。平方根のところだけは概算が煩雑ですし、計算精度をあまり落とさないために電卓を用いました。こうして結果を見立てておくと、プログラムが正しく作られているかどうかの確認を自信を持って行うことが出来ます。この計算結果を見ると、データファイルdata001.csvは非常に相関の高いデータであるといえます。このデータは、グラフにすれば回帰直線の近くで密集するでしょう。

今回はここまで

今回は、相関係数とは何かを大雑把に解説し、相関係数の計算を手計算で実施してみました。次回は測定データから相関係数を求めるプログラムを作成してみましょう。