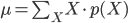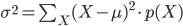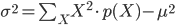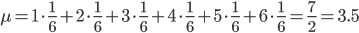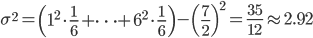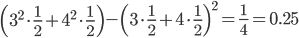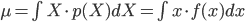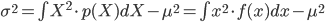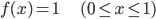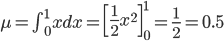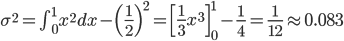今回と次回では前後編に分けて、統計においてもっともよく使われる確率分布である「正規分布」のお話をします。
第2回・第3回の復習
最初に、前回までのおさらいを簡単にしておきましょう。
まず確率を定義するものとして、確率変数 X と確率分布 p(X) を紹介しました。これが「確率」であるためには、以下の2つの重要な条件を満たしている必要がありました。
- 確率の値は0以上1以下
- すべての取り得る値の確率の合計は1
これらの条件は、今後機械学習を学んでいく上で、常に意識しておかないといけません。今回も使いますよ。
それから、確率変数が複数ある場合の「同時確率」「条件付き確率」「周辺確率」、そして「事後確率」を導入し、「確率の加法定理と乗法定理」という2つの定理と、「ベイズの公式」を導きました。加法定理と乗法定理については、今回も使いますのでその時に確認しましょう。
最後に、「条件付き独立性(ナイーブベイズ)」を仮定した文書分類モデルを紹介し、第3回では恩田さんによる実装例をご覧いただきました。今回は使いませんが、確率変数の独立性はとてもよく用いられる概念なので、これもしっかり覚えておいてください。
離散な確率と連続な確率
ところで前回までは明言していませんでしたが、確率変数の「取り得る値」が有限個(正確には「可算個」)であることを暗黙のうちに前提としていました。
このような「取り得る値が有限個」、または整数など「バラバラな数」で表すことができる確率を「離散確率」と言います。これまで例としてあげていた「サイコロを振って X が出る確率」や「文章に単語が含まれる確率(含まれるとき X=1、含まれないとき X=0 )」は有限個の場合しかとらない「離散確率」です。
一方、「目的地に X 分で着く確率」というとき、X は3分ぴったりかもしれませんし、3.5分(3分30秒)かもしれません。3.5714...分などいくらでも細かい時間の可能性だってあります。このような、確率変数の値を実数で表す確率を「連続確率」と言います。
ところで、なぜ「離散確率」と「連続確率」を分けて考える必要があるのでしょう? わざわざ分けているということは、何かが違っているはずです。
そこで、先ほどの連続確率の例「X 分で着く確率」を、あの「確率の重要な2条件」に当てはめてみましょう。話を簡単にするために、Xを3分から4分までに限定し、さらにその間ならどの時刻でも同じ確率で到着する、と仮定します。
まず仮定から、3分で着く確率と4分で着く確率は等しいです。
p(X=3) = p(X=4)
その中間の3.5分の確率も等しくなります。
p(X=3) = p(X=3.5) = p(X=4)
さらにそれぞれの中間の3.25分と3.75分の確率も等しくなります。
p(X=3) = p(X=3.25) = p(X=3.5) = p(X=3.75) = p(X=4)
実数はいくらでも間を分割できますから、この調子で X=3 と X=4 の間を無限回分割しましょう。
「どの時刻でも同じ確率で到着する」という仮定から、これらはすべて等しい確率を持つことがわかります。その確率を q とします。
ここで確率の条件「すべての確率の合計は1」を考えます。今、無限個の q を得ていますが、「すべての確率」には足りないかもしれませんので、その合計は1以下になるはずです。つまり、q × (無限個) ≦ 1 とわかります。しかし、そのような q があるとすれば q = 0 のみです!
したがって、確率 p(X) は常に0であるという結論になってしまいました。何を間違えてしまったのでしょうか……。
確率密度関数
実は、このような困ったことになってしまったのは、連続確率で p(X=3) や p(X=4) を考えようとしたことが原因なのです。
記号で書くと p(X=3) みたいなものが存在するかのように錯覚するかもしれませんが、言葉で表すと p(X=3) は「厳密に3分ぴったりで到着(誤差は完全に0!)」という意味なのです。そんなの、ありえない(ある意味、確率=0)ですよね?
通常の感覚では、こういう時「3分から3分半の間に到着する確率」というように、幅を持たせて考えます。
連続確率をそのように考えられるようにする方法が、これから紹介する「確率密度関数」です。
まず、確率変数 X の取り得る範囲で定義されている適当な関数 f(x) を考えます。f(x) はさすがに何でも良いわけではなく、満たすべき条件が2つありますが、それらの条件については後ほど紹介します。
この関数 f(x) を使って、X がある範囲 A に含まれる確率 p(X∈A) を「f(x) を範囲 A で積分した値」として定義するのです。
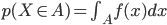
∫A は範囲 A に渡って積分を計算することを意味します。
例えば「3分から3分半の間に着く確率」 p(3≦X≦3.5) は、以下のように3から3.5までの定積分になります。
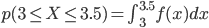
積分記号を見ると頭が痛くなる? では、グラフを使ってもう少し直感的に理解してみましょう。
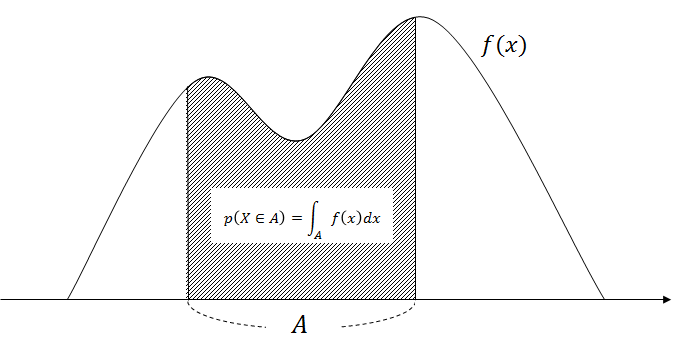
範囲 A での f(x) の積分値とは、グラフで見ると「A で表す範囲と f(x) によって囲まれる部分の面積」に他なりません。
A を広げると面積は大きくなり、A を狭めると小さくなります。これは、範囲 A を広げると、X が A に含まれる確率は大きくなる(3分10秒までに着く確率より、3分半までに着く確率は大きい)ということに対応します。
つまり「f(x) の面積=確率」ということですが、本当に大丈夫でしょうか?
面積は1より大きな値になる可能性が当然あります。またグラフに軸より下の部分があると、そこの積分値は「負の面積」になります。どちらの場合も確率値として適しません。
そこで、ちゃんと「面積=確率」と言えるようにするため、f(x) に2つの条件を与えます。
- 関数 f(x) の値は常に0以上
- 「取り得る値の全範囲」にわたって、関数 f(x) を積分すると1になる。つまり p(全範囲)=1 となる
第1条件は、グラフが軸より上にあるということなので、面積≧0 を保証してくれます。第2条件は、積分の最大値が1ということですから、面積≦1が言えます。これで「f(x) の面積=確率」と言えるようになりました。
これら2条件こそが、連続確率版の「重要な2条件」であり、それらを満たす f(x) を「確率密度関数」と呼びます。
それでは、先ほどからの連続確率の例「X 分で着く確率」を、「確率密度関数」で表してみましょう。X の範囲は3から4でしたから、その範囲で定義されている関数 f(x) を考えます。
最初は、まず簡単に「常に1の関数」にしましょう。
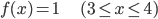
あとで説明しますが、これは「どの時刻でも同じ確率で到着する」ことを表しています。
この f(x) が第1条件を満たすのは明らかですし、また「取り得る値の全範囲」は 3≦X≦4 ですから、以下のとおり第2条件も満たしています。
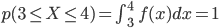
したがって、f(x) は連続確率 p(X) を定義する「確率密度関数」であると言えます。
この確率密度関数 f(x) を使って「3分から3分半の間に着く確率」を求めると、0.5 という直感通りの値が得られます。
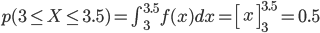
このように確率密度関数 f(x) は「積分すると確率になる」関数であるわけですが、そもそも f(x) 自体は何でしょうか。
勘違いしてはいけないのは、f(x) の積分値は確率ですが、f(x) の値は確率ではない、という点です。それが明快にわかる例を作ってみましょう。
同じく「X分で着く確率」ですが、今度は確率密度関数 f(x) として x が3分から3分半までは直線的に可能性が増え、3分半を過ぎると逆に減っていく、次のグラフのようなものを考えます。
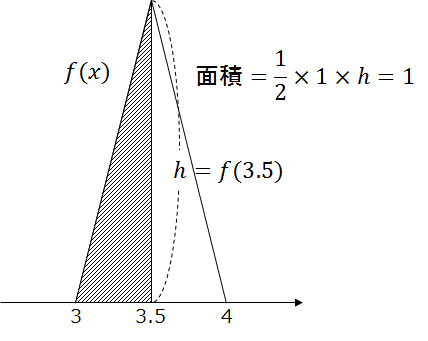
グラフより、「三角形」の高さ f(3.5) を決めれば f(x) が求まります。これは確率密度関数が満たすべき条件である p(全範囲)=1、つまり全体の面積が1になることから決まります。
この三角形の底辺の長さは1ですから、三角形の面積の公式を持ち出すまでもなく、その高さが2のときに面積が1になります。
つまり、この形の f(x) が確率密度関数であるためには f(3.5)=2 でなければならないわけです。「確率2」なんてありませんから、この確率密度関数の値 f(3.5) が確率にならないことは明らかですよね。
では確率密度関数の値 f(x) は何を表しているのかというと、確率変数が値 x をとる相対的な可能性を指していると考えられます。上のグラフで言えば、X=3.5 である可能性は X=3.25 である可能性の倍、などということを表しているわけですね。
値が相対的な可能性を表しているということは、定数倍してもそれは差し支えないということです。
そこで、確率密度関数 f(x) を定める際に、まずは可能性を表す関数を適当に作ったあと、p(全範囲)=1 となるように定数倍して調整するということができます。この操作を「正規化」と言い、確率密度関数を作る場合に非常によく行われます。
次回の後編では早速「正規化」を使いますので、憶えておいてください。
また、連続な同時確率 p(X, Y) を表す確率密度関数 f(x, y)、というように複数の確率変数に対しても同様に考えることができます。
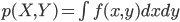
多変数関数に対する多重積分になりますので、厳密には細かいことをいろいろ示しておかなければなりませんが、ここでは面積が体積になったものとして理解しておいてください。
連続確率の加法定理
次に「確率の加法定理と乗法定理」が連続確率でも使えるかどうか、第2回の内容を復習しながら確認しましょう。
確率の加法定理
2個の確率変数 X,Y について、その同時確率 p(X,Y) と周辺確率 p(X) の間に以下の等式が成り立つ。
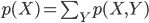
右辺のΣは、確率変数 Y のとりうる値すべてにわたって足しあわせる。
確率の乗法定理
2個の確率変数 X,Y について、その同時確率 p(X,Y)、条件付き確率 p(Y|X)、周辺確率 p(X) の間に以下の等式が成り立つ。
p(X, Y) = p(Y|X) p(X)
このうち、乗法定理については連続確率でも使えますが、加法定理はこのままでは連続確率で成立しません。連続確率では p(X=a, Y=b) という「点」の値が求められないのですから、「とりうる値にわたって足す」ということができるわけありませんね。
しかし確率密度関数は実によくできていて、この加法定理に出てくるΣを積分の∫に変えるだけで、連続確率版の加法定理が得られるのです。
連続確率の加法定理
つまり、連続確率版の加法定理は以下のようになります。
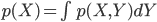
このとき右辺の本当の式は、同時確率 p(X,Y) の確率密度関数 f(x,y) を使って以下のように表されます。
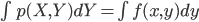
その際、この 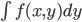 を
を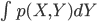 のように書いてもよい、という約束をします。これにより、離散確率と連続確率の差を「Σを積分の∫に変えるだけ」に収めることに成功しているわけですね。
のように書いてもよい、という約束をします。これにより、離散確率と連続確率の差を「Σを積分の∫に変えるだけ」に収めることに成功しているわけですね。
ここではとても簡易な説明で済ませていますが、実際には連続確率の両定理の定式化や証明は非常に大変です。その内容はこの連載の範囲をはるかに超えてしまっていますので、興味のある方は測度論の本などを参照してください。
確率の平均と分散
次は、確率の「平均」と「分散」です。第1回では、高校数学の「平均」と「分散」を前提知識として挙げさせてもらっていましたが、ここで簡単に復習しておきましょう。
まずは、p(X) が離散確率である場合について考えます。
p(X) の「平均」(または「期待値」)μ とは「確率分布の中心」を表す値の一つ、p(X) の「分散」σ2 は「平均を中心とした散らばり具合」を表す値の一つであり、それぞれ以下の式で定義します。
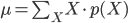
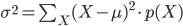
平均は、確率変数 X とその確率 p(X) の積の総和をとったものとして定義されます。サイコロのような確率が等しく1/6であるような例では、すべての場合の数を足して6で割るという、とても一般的な「平均」のイメージに一致します。
分散は「平均からのずれを2乗して平均したもの」になります。このことから分散は「平均を中心とした2次のモーメント」とも呼ばれます。2乗することでプラスマイナスがなくなり、しかもずれが大きいほど大きくなるので、分散は「値の散らばり具合」を表していると考えることができます。
ただ、実際に分散の値を求めるときに、この式は少し計算しにくいため、変形した以下の式を用いることが多いです。
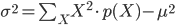
この式は「(二乗の平均)引く(平均の二乗)」という有名な憶え方がありますが、筆者はどっちが先だったかすぐに忘れてしまって、あまり役に立ったためしがありません(苦笑)。どうせ分散なんて自分の手で計算することは滅多にないので、憶えるなら意味を表す「平均からのずれを2乗して平均したもの」のほうが値打ちあります。
それでは、実際に平均と分散を求めてみましょう。例えば、1個のサイコロを振って出る目の確率分布 p(X) の場合は以下のような値になります。
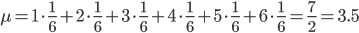
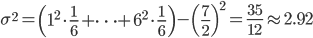
「平均」は感覚的にわかりやすいですが、「分散」が「散らばり具合」を表すというのは少々ピンとこないかもしれません。
そこで、1から6の目がある普通のサイコロと、3と4の目が3面ずつある特別なサイコロを考えてみてください。どちらのサイコロの場合も平均は3.5になります。ところが、特別な方のサイコロの分散は以下のようになります。
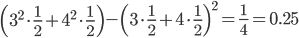
この値は、普通のサイコロの分散2.92よりかなり小さい値です。同じ平均でも、取り得る値の幅が小さいと分散も小さくなるわけですね。
「分散」の効用は正規分布を考えることでより一層明らかになるのですが、それは後編の楽しみに取っておきましょう。
今度は p(X) が連続確率である場合を考えてみましょう。連続確率 p(X) の平均と分散は、Σを積分の∫に変えた以下の式で定義されます。
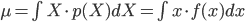
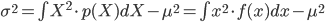
これらを計算することで実際の値を求められます。
身近な連続確率の例として、一般的なプログラミング言語ならまず備えている rand() 関数の「平均」と「分散」を求めてみましょう。
rand() 関数は、確率分布の目で見ると、0から1の間の一様な分布(どの値も同じ割合)にしたがって発生する乱数として考えることができます。
その確率分布を p(X)、確率密度関数を f(x) とすると、「0から1の間の」という条件から f(x) の値の範囲は0から1、「一様な分布(どの値も同じ割合)」という条件から f(x) は常に一定の値、そして「取り得る値にわたって積分すると1(面積が1)」という条件からその一定値が1であることがわかります。

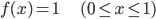
なお、これはとても簡単な「確率密度関数の推定」の例になっています。
このように必要な条件からその確率密度関数はどのような形なのか、どのような式で表されるかを調べるのは機械学習の重要なミッションの一つです。
話を戻して、この確率分布の平均と分散を求めてみましょう。以下のように計算できます。
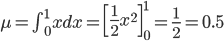
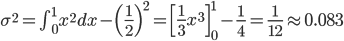
次回の後編ではいよいよ「正規分布」を紹介します。先ほどの rand() の平均と分散も次回にまた使いますので、お楽しみに。
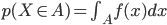
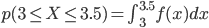

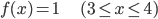
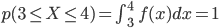
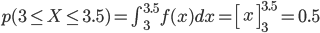

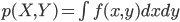

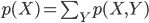
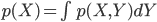
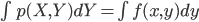
![]() を
を![]() のように書いてもよい、
のように書いてもよい、