統計的機械学習では解きたい問題にあわせて様々な分布を扱いますが、中でももっとも重要なのは、今回紹介する正規分布です。
まずはウォーミングアップ代わりに、前回のおさらいです。前回は、確率変数の値を実数のような「連続な数」で表す「連続確率」について説明しました。
連続確率は、サイコロの目ような「離散確率」とは異なり、「確率密度関数」というものを導入し、「確率密度関数 f(x) の積分値=面積=確率」として定義します。確率を「点」に対して考えるといろいろと都合が悪いので、「範囲」に対して考えるのでしたね。
分布が確率であるためには「足して1になる」などの重要な条件がありましたが、連続確率にも同様に「重要な2条件」があります。
- 確率密度関数 f(x) の値は常に0以上
- 「取り得る値の全範囲」にわたって、確率密度関数 f(x) を積分すると1になる。つまり p(全範囲)=1 となる
重要なポイントは、f(x) の値自体は確率ではない、積分(面積)を求めると初めて確率になる、という点です。
f(x) は相対的な可能性を表す数であって、だから適当な関数 f(x) を考えた後に、定数倍して p(全範囲)=1 となるように調整することで確率密度関数を得ることができるのでしたね。この調整を「正規化」と言い、この後早速登場します。
確率密度関数の考え方はとてもよくできていて、離散確率との本質的な違いをうまく吸収し、使い勝手の違いを「Σを∫に置き換えるだけ」で済ませられるのでした。第2回で紹介した、離散確率についての「加法定理と乗法定理」も、「Σを∫に置き換える」と連続確率版を得ることができました。
また、確率分布の「平均(期待値)」と「分散」についても紹介しました。こちらは本文の中でもう一度出てくる時に復習しましょう。
正規分布
さて、いきなり天下りですが、以下のグラフで表される確率密度関数 f(x) で定義される連続な確率分布 p(X) を考えてみましょう。
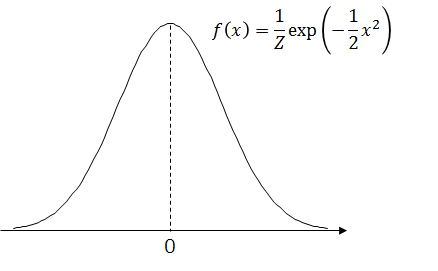
このグラフは中心が高く、両側は徐々に下がった後なだらかになって、軸に沿う形で長く伸びています。
この形はよく「釣鐘型」と呼ばれるのですが、「釣鐘」というと日本人にはお寺の鐘の印象が強いでしょうから、裾が長いこの形をなぜ釣鐘というんだろう、と不思議に思うかもしれません。実は、元の英語では「ベルカーブ」、つまり口が開いたベルを伏せた形に見立てて名付けられたため、不自然なのは日本語訳なんですよね。……と、話がわき道にそれてしまいました。
確率密度関数の値は、さきほどのおさらいでも触れましたが、「相対的な可能性」を表します。つまり、確率密度関数がこのようなグラフになるということは、中心付近の値は非常に発生しやすく、そこからある程度離れると急速に発生しにくくなる、そういう連続確率を表している確率密度関数であるということがわかります。
このようなグラフを描く確率密度関数は以下の式で与えられます。
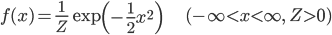
exp は自然対数 e=2.718... の指数関数です。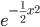 と書いてもいいのですが、字が小さくなって読みにくいからか、機械学習でそちらの書き方を見掛けることは少ないようです。
と書いてもいいのですが、字が小さくなって読みにくいからか、機械学習でそちらの書き方を見掛けることは少ないようです。
expの性質から f(x)≧0 がわかります。Z は「全範囲で積分して1」の条件を満たすように適当に調整します。このような Z を「正規化定数」と言います。
Z を求めるには、f(x) から 1/Z を取り除いて積分をして計算します。この積分の計算には少々パズル的な方法を使う必要があるのですが、詳細は省略します。
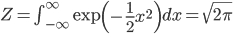
求めた Z で積分の両辺を割れば、「f(x) の積分=1」になってくれるのはわかります。こうして確率密度関数が「全範囲にわたる積分=1」を満たす正規化定数を求めることを、「確率密度関数の正規化」と言います。そして、このようにして構成された釣鐘型の連続確率分布が「正規分布」です。
19世紀の偉大な数学者カール・フリードリヒ・ガウスが正規分布を使った研究を行ったことから「ガウス分布」とも呼ばれます。最初に正規分布というものを導入したのはド・モアブルなのですが、最初に考えた人とは違う人の名前が定着してしまうのは科学ではよくあることですね(苦笑)。
「正規分布」はよい性質を数多く持っており、もっともよく利用される連続な確率分布の一つです。その性質や、より一般的な定式化について、このあと順に確認していきましょう。
正規分布の平均と分散
確率変数の「平均」(期待値)と「分散」を前回紹介しました。復習を兼ねて、もう一度振り返っておきましょう。
確率変数 X とその確率分布 p(X) が確率密度関数 f(x) によって与えられるとき、X の平均 μ と分散 σ2とは以下の式で定義されるものでした。
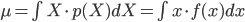
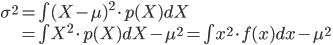
ここでは連続確率の場合の定義式を示していますが、離散確率の場合は積分の∫が和をとる記号のΣに置き換わるのでしたね。
それではこの定義式を使って、先ほどの正規分布の平均と分散を求めてみましょう。
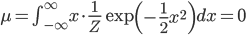
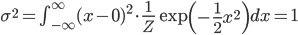
平均が0、分散が1という、とてもキリのよい分布だったのですね。
この平均0、分散1の釣鐘型を平行移動&横に引き延ばしつつ、正規化定数を調整することで、与えられた平均と分散を持つ、より一般的な正規分布を考えることができます。
そのようにして構成した平均が μ、分散が σ2 である正規分布の確率密度関数は以下のようになります。
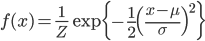
ただし
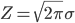
ここでの最大のポイントは、「平均」と「分散」というたった2つの値が与えられるだけで、正規分布の全体が決まるということです。
そのおかげで、全く未知の確率分布に対しても、とりあえず平均と分散だけでもわかっていれば、正規分布と仮定して試しに計算してみるということができます。これは機械学習を含む統計的分野では結構ポピュラーな手法となっています。
それどころか、平均と分散すらわかっていないのに「とにかく正規分布だとしたら」と仮定して、平均と分散を推定する、という手法もあるくらいです。
中心極限定理
しかし、「未知の確率分布を正規分布と仮定してしまう」というのはあまりにも乱暴過ぎるように感じます。それに、何か扱いやすい分布で近似してしまいたいというだけなら、どうしてそれが正規分布なのでしょう。平均と分散で決まる分布でいいなら、他にもありそうです。
実は、数ある「よく使う分布」の中でも正規分布はとびきり特別な存在なのです。それを示してくれるのが「中心極限定理」です。
「中心極限定理」とは、どのような分布であろうとも、その試行を独立に繰り返して得た値の合計は、正規分布に近付くというものです[1]。
つまり、コインの表が出る回数とか、サイコロの目とか、テストの点数とか、身長や体重とか、電車の遅れる時間とか、その他どのような分布でも、繰り返しの回数が十分大きければ正規分布とみなせる、というとんでもない定理なのです。
このとても不思議な「中心極限定理」が本当に正しいということを、サイコロを使って実感してみましょう。
サイコロの場合、「試行を独立に繰り返して得た値の合計」とは、同時に複数個のサイコロを振って出た目を合計することに相当します。そこで、サイコロを1個、2個、4個、10個それぞれを100,000回振って、目の合計のヒストグラムを描いてみたのが以下のグラフです。
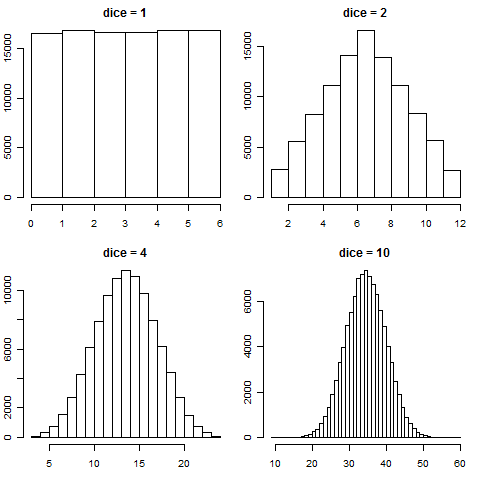
1個では横一直線(すべての場合が同じ確率の一様分布)だったのが、サイコロの個数を増やすにつれて裾の長い釣鐘型(正規分布)に近付くのが見てとれるでしょう。
もう一つの例として、前回計算した rand()関数の平均と分散に再登場してもらいます。
一般的なプログラミング言語なら必ず備えている、0から1の間の乱数を返すrand()関数は、確率分布として見ると、0から1で定義された以下の確率密度関数 f(x) によって与えられる連続確率分布でした。
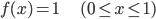
そして、その平均と分散は以下のようになることを計算しました。
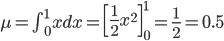
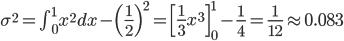
紙数の関係でここでは詳しく述べませんが、確率変数の和の平均と分散は、元の平均と分散のそれぞれの和に等しいことがわかっています。
つまり、以下の式から、平均が 12*1/2-6=0、分散が 12*1/12=1 の正規分布にとても近い分布に従った乱数が生成される、ということがわかるのです。
# 12個のrand()から6引く
r = rand()+rand()+rand()+rand()+rand()+rand()+rand()+rand()+rand()+rand()+rand()+rand()-6
実際、この式は正規乱数(正規分布に従う乱数)が欲しいけれど、その機能が用意されていない場合、簡易に正規乱数を得る方法としてよく用いられます。
ただしそのとき、「rand() を12個並べるなんてカッコ悪い……。まとめて 12*rand() にしよう」とやってはいけませんよ! サイコロを1個振ってその値を12倍するのと、12個のサイコロを合計するのとでは全く違いますからね。
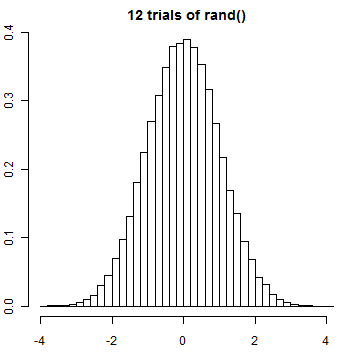
この「rand() 12個マイナス6」のヒストグラムも確認しておきましょう。確かに釣鐘型のグラフになっていますね。
「よく使う分布」はどうしてよく使う?
「中心極限定理」という強力な定理のおかげで、正規分布はとてもよく使われるということはわかりました。
しかし、「よく使う分布」は実は他にもいくつもあります。以下に代表的なものだけでもあげてみましたが、数えだしたら結構止まりません。
- 二項分布
- 多項分布
- ガンマ分布
- ベータ分布
- ディリクレ分布
- ……
これからの連載の中でこれらの分布を紹介する機会もあるでしょうから、一つ一つがどのような分布であるかはひとまず置いておきましょう。
ここでは、なぜ「よく使う分布」はこんなにあるのか、という話をしておきたいと思います。
まず第一の疑問は「よく使う分布なんて、正規分布だけで足りないの?」というところでしょうか。中心極限定理を見た後だと、確かにそんな気もしてきます。
ところがそういうわけにもいかない理由として、中心極限定理にしたがって正規分布に近づけるには、試行の繰り返し回数が十分大きい必要がある、という点があげられます。
また、先ほどのサイコロを4個振ったグラフではかなり正規分布に近づいていましたが、これはサイコロが単純な一様分布だからです。一般にはもっと多くの試行が必要なのです。
しかも、中心極限定理の「独立に繰り返す」というのが非常に強い制約なのです。例えば英文で "He" という単語の後に "is" が続く可能性は高そうですが、"am" や "are" が続く可能性はほとんどありません。
このような他の値との依存性が高い(独立ではない)試行は、何回繰り返しても正規分布に近付きません。そのような「正規分布に近づきそうにない分布」を扱うときはどうすればいいでしょう。
もっとも望ましく思えるのは、一切近似を行わない、という案です。しかしそんなことをしようとすれば、パラメータ数が現実に扱える範囲を簡単に超えてしまいます(第2回のナイーブベイズモデルの導入を思い出してください)。
そこで「よく知っている(=計算しやすい)分布の中から、できるだけ似ているものを選んで、それを使う」という手が用いられるのです。
このとき、「どの分布に似ているの?」という疑問に答える必要があるため、「こういう状況(モデル)では、この分布を使う」というパターンをあらかじめいくつも想定しておきます。これが「よく使う分布」がいくつも存在する理由なのです。
多次元正規分布
最後に、正規分布の多次元版を紹介しておきましょう。
正規分布は複数の確率変数に対しても考えることができます。このとき難しくなるのは、1次元(1変数)では分散が1つの値で済んでいたのが、多次元(2変数以上)になると「共分散」という対称行列になることです。
まずは天下りですが、多次元正規分布を定式化する式を確認してみましょう。X がD次元の正規分布に従う確率変数のとき、確率分布 p(X) を与える確率密度関数 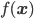 は次の式で与えられます。
は次の式で与えられます。
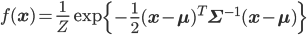
ただし
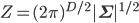
D個の値からなる確率変数 X はベクトルとして表現されます。したがって対応する 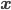 と平均
と平均 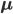 もD次のベクトルになります。ベクトルは太字で記し、肩にTを書いてベクトルの転置を表します。
もD次のベクトルになります。ベクトルは太字で記し、肩にTを書いてベクトルの転置を表します。
Σは「共分散行列」と呼ばれるD次の対称行列で、いわば多次元版の分散です。イメージとしては、各変数間にどれくらい関連があるかを行列の形に並べたものになっています。|Σ| は共分散行列の行列式、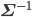 は共分散行列の逆行列を表します。Zはこれまでと同じく正規化定数です。
は共分散行列の逆行列を表します。Zはこれまでと同じく正規化定数です。
式で使われている記号を説明するだけでこのように一仕事なのですから、この式をパッと見ではよくわからないのも無理ありません。そういうときは、一番重要な部分をしっかり見ておくことです。
この式の「一番重要な部分」は、exp()の中身です。正規分布の平均と分散(共分散)は exp() の中身で決まります。そして正規分布は平均と分散(共分散)で決まってしまうわけですから、確かににこの部分が正規分布の本質で間違いなさそうです。
この形の式は「2次形式」と呼ばれます。ベクトルと行列の積を展開するとxの2次式が得られるからです。つまり、正規分布とは「expの中に2次形式が入っている分布」と言うこともできます。
ちょっとした言い換えのようですが、実はこれは正規分布のとても重要な特質なのです。正規分布のより深いところを学ぶときには、むしろこの「expの中に2次形式が入っている分布」というほうが正規分布そのものという印象に変わってくるでしょう。
2次元正規分布のグラフを確認しておきましょう。
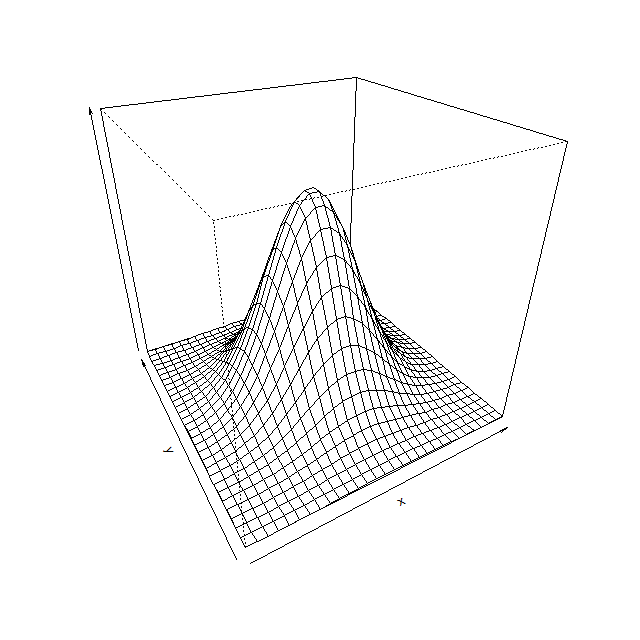
2次元なので平面の広がりがある点が1次元と違っています。しかしその当然の違いを除けば、「裾が広くて長い釣鐘型の分布」という形状を受け継いでいることがわかります。
ただし、一般の多次元正規分布はパラメータの数は少なくありません。
n次元の正規分布は、その平均と共分散で記述することができますが、平均はn次のベクトルなのでn個のパラメータ、共分散はn次の対称行列なので n(n+1)/2 個のパラメータが必要となってしまいます。
今回のまとめ
2回にわたって連続分布と正規分布を紹介しました。
具体的な機械学習のお話からちょっと離れてしまっているように思えるかもしれませんが、今後の内容を理解するためにとても重要な基礎知識になります。
特に確率密度関数やその正規化はこれから何度となく付き合っていきますので、わからなくなったらここに戻って確認してくださいね。
次回の実践編では、いろいろな分布を扱うためコード例を見ていただく予定です。
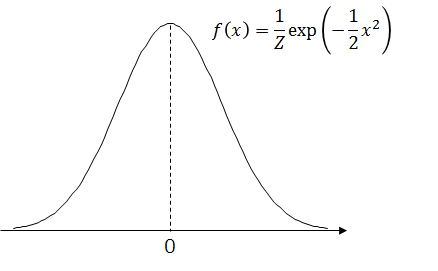
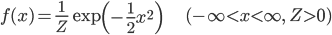
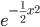 と書いてもいいのですが、
と書いてもいいのですが、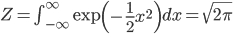
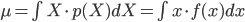
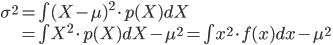
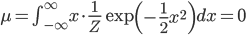
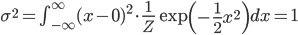
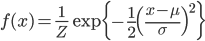
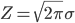

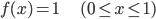
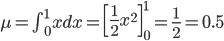
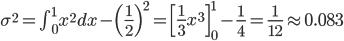

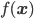 は次の式で与えられます。
は次の式で与えられます。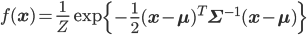
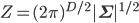
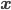 と平均
と平均 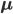 もD次のベクトルになります。ベクトルは太字で記し、
もD次のベクトルになります。ベクトルは太字で記し、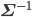 は共分散行列の逆行列を表します。Zはこれまでと同じく正規化定数です。
は共分散行列の逆行列を表します。Zはこれまでと同じく正規化定数です。



