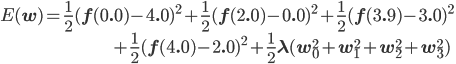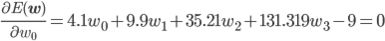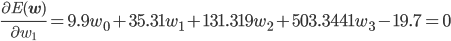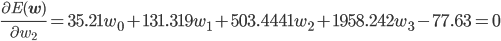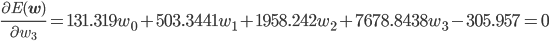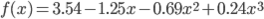前回の前編 では「最小二乗法」を紹介する中で、機械学習は数多くのことを仮定して、その中で一番良い答えを見つけるものだということを見てもらいました。
特に「最小二乗法」でデータ点から直線を推定する場合、次の3つのことを仮定していたことを学びました。
変数間の関係を関数で表す
関数のモデルは直線(1次式)を考える
パラメータを選ぶ指標として二乗誤差を用いる
今回はこれらの仮定を振り返りながら、一般化された、より柔軟な機械学習の手法を紹介しましょう。
戻らないけど「回帰」
先ほどの仮定の1番目、「 変数間の関係を関数で表す」ことを機械学習では「回帰」と呼びます。つまり機械学習の世界で「回帰問題を解く」といった場合は、この仮定をしていることになります。
「回帰」という言葉の由来
「どうして関数を求めることを『回帰』と呼ぶの? 何か戻るの?」と思うかもしれません。この名前は、もともと「平均回帰」という現象を説明する手法として初めに導入されたのですが、応用を繰り返すうちに使われ方が変化していき、「 回帰」という名前だけが残ってしまったのです。
英語版のWikipediaの回帰(Regression)の項 では、「 回帰」の歴史的な経緯についてもう少し説明されていますので、気になる方は読んでみるとおもしろいでしょう。
変数が2個の回帰問題
ここで、最初に「変数が2個の回帰問題」を、少しきちんとした言葉で定式化しておきましょう。
実数をとる入力変数の値 xn と目標変数の値 tn の組 (n=1,...,N) が与えられているとき、すべての n について f(xn )=tn (n=1,...,N) を満たす関数 f のうち「もっとも適切なもの」を求める
ただし、値には誤差が含まれていることも考慮することが望ましい
回帰問題のポイントは、「 わかっている値が有限個」と「値の誤差」です。実はそれぞれが2番目と3番目の仮定に対応してます。
一般に仮定は弱ければ弱いほど良いですよね。2番目の仮定「関数のモデルは直線(1次式)を考える」は少し強い(狭い)ので、これを弱めてもう少し表現力の高い関数を使えるようにしたいところです。
しかし、有限個の点から決まる実数関数なんて無数に存在するため、弱めすぎるわけにもいきません。データ点さえ通ればいいのなら、フリーハンドで書いたようなぐにゃぐにゃのグラフでも、あるいは単純に各点を直線で結んだ折れ線グラフでも問題ないということになります。
それから前回、二乗誤差の最小化は、各点での誤差の分散を最小化してくれることを説明しました。すると3番目の仮定は、各点にできるだけ同じくらいの誤差がのるように調整するということになるため、こちらは一定の必然性があると言えそうです。
線形回帰
そこで、目下の関心は2番目の仮定「関数のモデルは直線(1次式)を考える」をどのように弱めることができるか、という点に絞って考えましょう。
その答えの一つが、これから紹介する「線形回帰」です。「 線形」とついていますが、これは関数のモデルが1次関数(直線)ということではなく、モデルの式が線形結合の形をしているためです。
基底関数
「線形回帰」では、まず「基底関数」というものを定めます。文字通り、関数を表現するベースとして使うものです。基底関数に特別な条件はないので自由に好きな関数が使えるのですが、中でもよく使われる基底関数2種類を紹介しましょう。
多項式基底:
ガウス基底:
多項式基底は文字通り「多項式で表される関数を想定する」ための基底です。
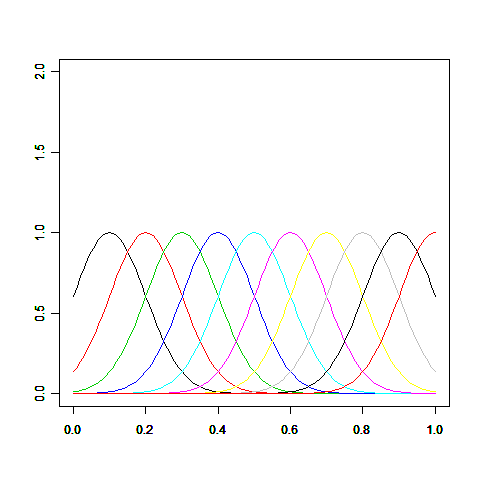
ガウス基底はデータ点の情報を近い距離に効率的に反映させることのできる基底で、次の図のように釣鐘型になっています。exp()の中身が2次式なところが正規分布の確率密度関数と同じですが、基底関数は確率ではないので正規化(面積=1)は行っていません。ガウス基底のパラメータμと s は適当に選びます。例えばμを0.1、s を0.1から1.0まで0.1刻みに選んだ場合、ガウス基底のグラフは次のようになります。
それぞれ表現できる範囲が違いますから、一概にどちらが良い基底関数であるとは言えません。ここまでの話の流れを踏まえてもらっていれば、「 ああ、なるほど、今度はここからが仮定になるんだね」とピンとくるのではないでしょうか。
以降の説明ではわかりやすさを優先して多項式基底を使いますが、求めたい関数についての情報が少ない場合などは、まずガウス基底を試してみるのが良いかもしれません。
線形回帰の求め方
この基底関数は最初に決めて固定し、その線形和を求めたい関数 f(x) とします。各基底関数に与えられる重み wi をパラメータとすることで、「 想定する関数の集合」を得ることができます。
パラメータ wi を決定すれば f(x) が求まりますので、wi を適切に決める方法があればいいのですが、それには引き続き二乗誤差を使うことにしましょう。ただし一般的な記法にあわせて、二乗和を2で割ったものを使います[1] 。
一見複雑ですが、xn と tn が定数であることを思い出せば、これは単なるwi の2次式です。したがって、これを最小にするwi を求めることができて、求めたい関数 f(x) も決まります。
これが「線形回帰」の基本的な流れです。
線形回帰の例
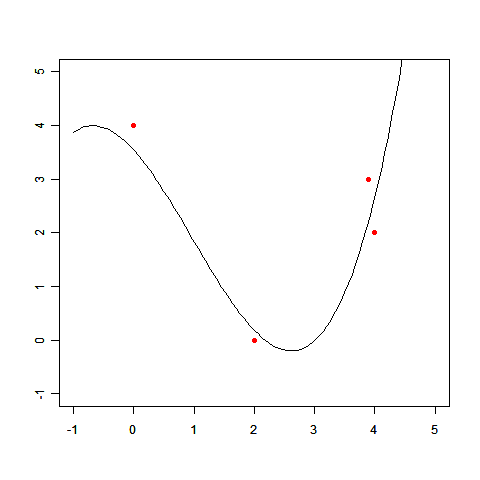
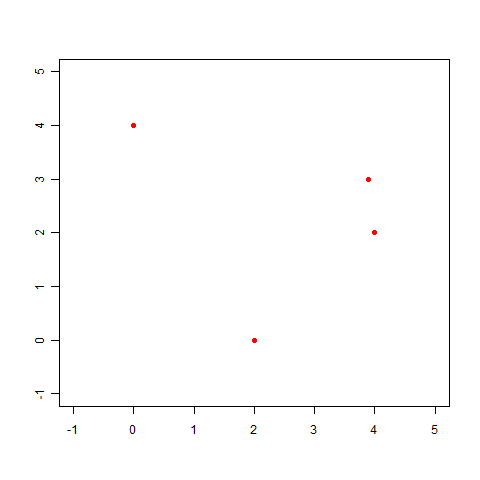
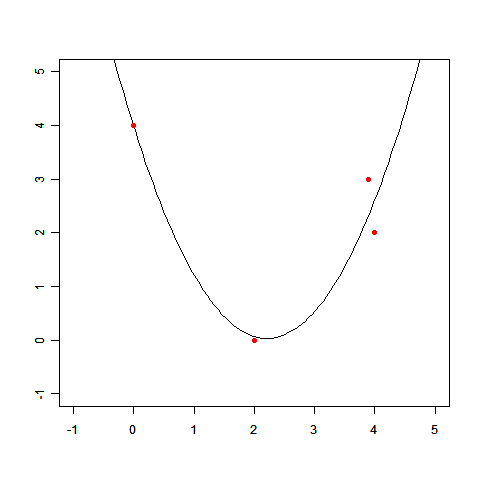
直線で表せない例として前回登場した、次のデータを使って、実際に線形回帰を解いてみましょう。
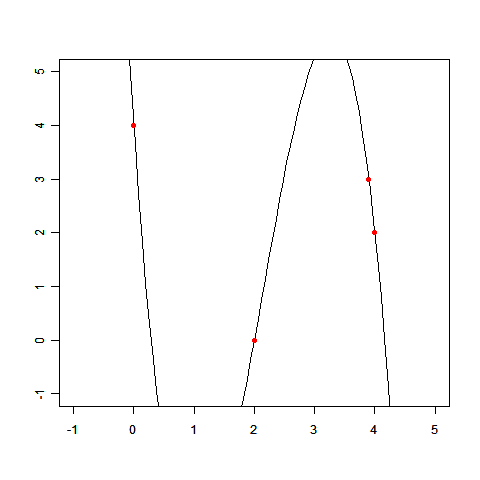
(x,t)=(0.0,4.0),(2.0,0.0),(3.9,3.0),(4.0,2.0)
このxとtの関係を、多項式基底の線形回帰で求めます。基底関数には φ0 =1, φ1 =x, φ2 =x2 の3個の多項式を使いましょう。求めたい f(x) はその基底関数の線形和として表わされます。
w0 , w1 , w2 を適切に決めるのがここの目的です。この f(x) と点列を使って、誤差関数を求めましょう。誤差関数には先ほど紹介した二乗誤差を用います。
後はこの式を平方完成すればいいのですが、項数が多すぎてちょっと計算が大変です。そこで、誤差関数が最小となる wi では偏微分が0になることを使って[2] 、最小値を与える wi を求めることにしましょう。
同様に、
この連立方程式を解けば、w0 =3.98, w1 =-3.58, w2 =0.80 が求まります。
ここでは原理を見てもらうためにわざわざ泥臭い計算に落としていますが、実際には行列を使ってもっと機械的に計算ができる方法があります。そのあたりは次回の実践編で紹介されると思います。
求めた wi を使って、f(x) のグラフを描いてみましょう。
このとおり、だいぶそれっぽい線が描けました。
過学習(over-fitting)
先ほどの例では、多項式基底の個数を3個(つまり2次式)にしましたが、これは自由に選ぶことができます。
一般に基底関数の個数が多いほどモデルとしての表現力、つまり記述できる関数の幅は広がりますので、計算が大変でない範囲でできるだけ基底を増やせばいい気がしますが、残念ながら話はそう単純ではありません。
試しに先ほどの例題にて、基底関数を1個増やして1, x, x2 , x3 の4個で解いてみましょう。
誤差関数の偏微分は w0 ~ w3 のそれぞれで行うため、4元の連立方程式が得られます。
これを解くと、w0 =4.00, w1 =-16.91, w2 =10.81, w3 =-1.68 が求まりました。グラフを描いてみましょう。
どうでしょう、「 それっぽい」と言えそうですか? もちろん「そうそう、こういう答えが欲しかったんだ」という人がいないと断言はできませんが、やはり通常はこのような極端な答えは望ましくないでしょう。
関数がこのようになってしまうこと、より一般には「データに適合しすぎてしまうこと」により「都合の悪い答え」(都合いい悪いも仮定)が出てくることを「過学習(over-fitting) 」と呼びます。
過学習を防ぐ正則化
回帰問題では、データに対してモデルの表現力(自由度)が不釣り合いに高いと過学習が発生しやすくなります。
実際、多項式基底なら、基底関数の数がデータ点より多ければ、すべての点を通る関数が作れてしまいます。
つまり、過学習への対策としては基底関数を「適切に」設定すれば良いわけですが、一般にそれはとても難しい問題です。
なぜなら適切な基底関数がわかるということは、求めたい関数がどういう形なのか、だいたいわかっているということになります。しかし問題を解く前に、それを知っているわけありません。
また、基底関数を多くしておいて、過学習が発生したら減らしていく、というアプローチも考えられます。
しかし、2次元3次元くらいなら良いのですが、高次元になるとグラフなんかとても描けず、したがってそもそも過学習が発生しているのかどうかが判断しづらいということも少なくないのです。
一方、先のグラフからもわかるとおり、求めた f(x) は与えられた点をピッタリ通っているので(誤差0!) 、数字だけ見ればこの答えはむしろ良い答えになってしまいます。
要するに、今入っている3つの仮定だけでは足りないということなんです。過学習に対抗するための仮定が何かもう一つ必要ということになります。
正則化項の導入
それを踏まえて、先ほど求めた f(x) の式をもう一度よく見てみましょう。すると、w1 とw2 がすこし大きめの値(0から離れた値)になっていることに気づきます。
係数が大きいと、跳びはねるようなグラフになりやすいです。そして過学習が起きている時、グラフはおおむねそのような挙動を示します。
そこで、パラメータが大きくなり過ぎたら「ペナルティ」がつくという仮定を入れてみましょう。
ここでは理屈はとりあえずおいといて、単純にペナルティとして「パラメータの二乗和」を誤差関数に付加してみます。
パラメータが大きくなると、ペナルティ この新しい誤差関数全体をできるだけ小さくすることは、小さめのパラメータを選ぶ効果が期待できます。
この追加したペナルティ項を「正則化項」と呼びます。
λは「正則化係数」と言い、ペナルティの効き具合を調整するパラメータとして働きます。λが大きいほど、より小さい wi を選ぼうとするでしょう。
すると、「 今度はλをいくつにすればいいか」「 正則化項はどんな形がいいか」などの問題が発生してしまいますが、ここでは深入りしないことにします。
余談ですが、ペナルティを「正則」と呼ぶことに個人的にはひどく違和感があります。もともとは「不良設定問題」を「良設定問題」にする、くだいて言えば「本質的に解きにくい問題を解きやすくする」ために導入された概念だったので、「 正則化」という偉そうな名前がつけられたのです。ペナルティ項だけ見ていると、そんな面影を感じさせてくれませんけどね……。
正則化つき線形回帰
最後に、先ほどの例を正則化項つきで解いてみることで、期待した通りに働くことを確認しましょう。
誤差関数に正則化項が加わりました。先ほどと同様に偏微分から連立方程式を得て、それを解きます。このとき、正則化係数λは0.1としています。
これを解くと、w0 =3.54, w1 =-1.25, w2 =-0.69, w3 =0.24 となります。
先ほどの答えが w0 =4.00, w1 =-16.91, w2 =10.81, w3 =-1.68 だったので、確かにずっと小さい(0に近い)値になってくれましたね。
それではグラフを描いてみましょう。
極端に飛び跳ねるようなグラフではなくなり、確かに過学習が抑えられている(都合の悪い答えではなくなっている)ようです。
まとめ
線形回帰は、シンプルで計算が簡単、それでいて一定の柔軟性を確保しつつ、柔軟になりすぎたときの手当もできる、という機械学習のお手本みたいな手法です。
ただしその過程では、非常に多くのことを仮定していることも見ていただきました。ここまでに登場した仮定をもう一度まとめてみましょう。
変数間の関係を関数で表す
関数のモデルは基底関数の線形和を考える
基底関数には多項式(もしくはガウス基底など、何か決まったもの)を用いる
パラメータを選ぶ指標として二乗誤差を用いる
過学習を抑えるためにペナルティ(正則化項)を導入する
正則化係数には0.1(あるいは何か決まった小さな値)を用いる
くどいようですがもう一度念を押すと、これらの条件は与えられたデータから単純に導かれたりとか、他には方法がないことが証明されていたりとか、そういうことは一切ありません。あくまで、問題を解きたい人が仮定として設定することで、初めて「正則化つきの線形回帰」になるのです。
次の第10回は実践編、線形回帰の実装を紹介する予定です。理屈でぐるぐるになった頭に、ホッと一息ついてもらえるはずです。お楽しみに!
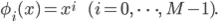
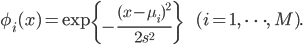
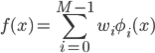
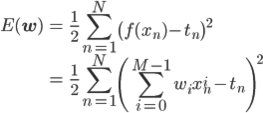
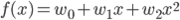
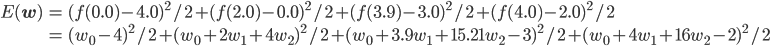
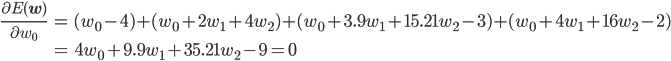
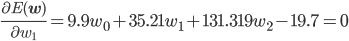
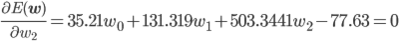
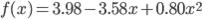
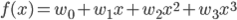
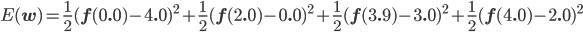
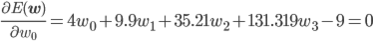
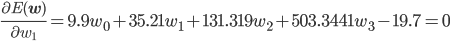
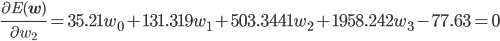
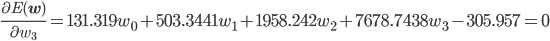
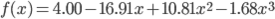
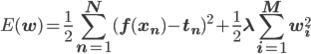
![]() も大きくなってしまいます。したがって、
も大きくなってしまいます。したがって、