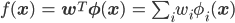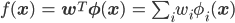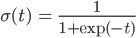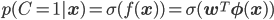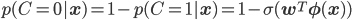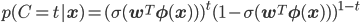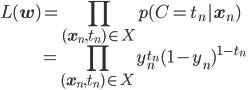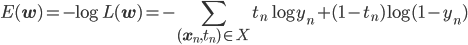前回までに、分類問題のモデルの一つ「パーセプトロン」を紹介して、その実装を行いました。
パーセプトロンはとてもシンプルでわかりやすいモデルでしたが、「線形分離可能」なデータにしか適用できないという難点がありましたね。
今回は線形分離できないデータにも適用できる分類モデルとして、「ロジスティック回帰」を紹介します。
予測の信頼度
分類器を使って、実際の問題を解くときのことを考えてみます。例えば「メールのスパムフィルタ」などが想像しやすいでしょう。
一般的にスパムフィルタでは、データであるメールを「スパム(迷惑メール)」と「スパムではない(通常のメール)」のどちらかに分類します。そこで、ちょうどパーセプトロンのような2値分類器を使えば無事解決……とは、なかなかいきません。
スパムフィルタを通り抜けてしまった迷惑メールを一つ一つ消す、反対に必要なメールが間違ってスパムと判定されてしまい見逃していた、などという経験がありませんか。
このように、機械学習による予測にはどうしてもある程度の間違いが含まれがちなので、その対策が必要になります。
例えば予測に自信がない場合はスパムに分類しないことで、「必要なメールをスパムと誤判定する」可能性を小さくするというのも一つの手です。そのためには、予測の信頼度をなんとかして測る必要があります。
そういう「予測の信頼度が出せるといいな」という頭で、パーセプトロンの判別式を復習してみましょう。
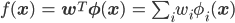
パーセプトロンはこの判別式f(x)の値が正か負かでデータ点の分類を推定する2値分類器でした。
この判別式からはもちろん符号だけではなく値の大小も得られますから、それを「信頼度」として使うことができそうな気がします。例えばf(x)が+0.00001なら正ではあるけれどあんまり自信なさそう、逆に+100000なら同じ正の予想でも確実な推定であるように思えますよね。
ところが残念なことに、パーセプトロンの判別式の値を信頼度と見なすのはお勧めできません。というのも、パーセプトロンの学習では符号さえ正しければパラメータの更新を全く行わないからです。
例えば正解が正のデータに対する予測値が正しければ、それが+100000であっても+0.00001であってもパラメータを更新しません。
つまり値の正負は学習しますが、値の大小は学習しないのです。これでは値の大きさが信頼度を表しているのか、たまたまそうなっているだけなのか判断できません。
ちなみに、「正解なのに+0.00001なんて小さすぎるから、そういうときに判別式の値が大きくなるようにパラメータを更新しよう」といったような改良版パーセプトロンもいくつかあります。この連載では紹介しませんが、代表的なモデルとしては"Passive Aggressive"や"AROW"などがあげられます。
判別関数を確率化
ここでは、分類モデルを確率化することで「信頼度」を組み込む方法を考えることにします。
例えば「正に分類される確率」をpとすれば、「負に分類される確率」は1-pになるため、確率の大きいほう、つまりp>0.5なら正、p<0.5なら負を予測とすればいいでしょう。
またこの確率の値pは、そのまま「信頼度」として扱うこともできます。正への分類をできるだけ確実なものにするには、判断の閾値を0.5より大きい0.7などに調整します。
では分類モデルをどのすれば確率化できるか考えるために、もう一度パーセプトロンの判別式を見てみましょう。
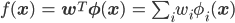
この式の値は明らかに確率にはなりようがありません。確率の値は0から1の間であるのに、この式は実数のどんな値でも取り得るからです。
そこで実数全体を確率の範囲である0から1に押し込めてしまう関数σを用意します。ちなみにこのσは「シグモイド関数」または「ロジスティック関数」と呼ばれています。
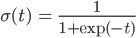
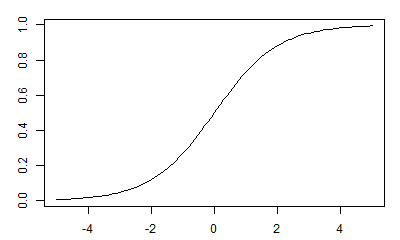
シグモイド関数σはこのようになだらかに0から1まで変化する関数です。
このσにf(x)を放り込んで、新しい関数p(x)=σ(f(x))を作ります。このp(x)の値は0から1の範囲に入りますから、確率として考えることができるようになるわけです。
「えっ、なにそれ。0から1の間ならそれだけで確率だなんて、いくらなんでも乱暴すぎるでしょう。本当にそんなことしていいの?」と思われるかもしれません。f(x)はただの線形結合、σはexpとかが入っている謎の式。確かにこれを見る限りでは確率っぽさは全く感じられません。
本当にp(x)を確率としてしまっていいのか、とてもとても気になるところかと思いますが、その説明は次回に譲ることにして、ひとまずはこのp(x)=σ(f(x))を「xが正に分類される確率」と考えるという仮定を認めて先に進むことにします。
大丈夫、その宿題は次回きちんとやっつけますし、他にわかりにくい仮定は出てきませんから、安心してください。
ロジスティック回帰
先ほどの仮定から出発して、確率的な分類モデルを構築してみましょう。
定式化のために、データ点xの分類を表す2値の確率変数をCとおきます。例えば問題がスパム判定なら、Cは「メールxがスパム(C=1)か、スパムではない(C=0)か」という確率変数になります。
パーセプトロンでは分類の値を正と負で表現しましたが、これから紹介するロジスティック回帰では1と0を使うほうが都合いいため、Cの値も同じく1または0とします。
この確率変数Cを使うと、先ほどの仮定は「xについてC=1となる確率となる確率はσ(f(x))」と言い換えられます。これを式で記述します。
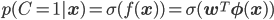
C=0となる確率は足して1になることから次のように記述できます。
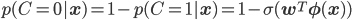
Cの値が1の場合と0の場合に分けるこの表し方は、わかりやすいのですが、代入して使うときには不便で困ります。
そこで、Cの取り得る値tが0か1しかないことをうまく利用して、次のように1つの式で記述することにします。
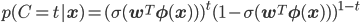
すこし長くてややこしいですね。簡単のためy=σ(wTφ(x))とおいて、次のように書き直しておきます。

これはt=1のとき、後半は0乗になって消え、前半のyのみ残ります。t=0のときは、前半が0乗になって後半の1-yのみ残ります。場合分けがうまくまとまっていますね。
この式を使えば、パラメータwを最尤推定するための尤度関数を表現できるようになります。
X={(xn,tn)}をデータ点xnが正解tnを持つデータセットとし、xnに対応するyn=σ(wTφ(xn))も同様に考えると、尤度関数L(w)は次のようになります。
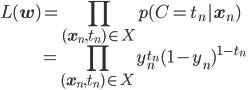
尤度関数の最適化
最尤推定とは実際に観測されたデータが確率最大となるようにパラメータを決める、つまりL(w)が最大となるwを見つけることです。
機械学習の周辺では、関数の最小点(または最大点)を求めることを「最適化」というのでしたね。特に連載第16回ではその最適化手法の一つとして「確率的勾配降下法」を紹介しました。この「確率的勾配降下法」でロジスティック回帰モデルを解いてみることにしましょう。
そのためにはまず、最小化(または最大化)したい目的関数を微分して「勾配」を得る必要があります。
ところが、尤度関数は「複数ある観測データのすべてが起こる確率」であるため、L(w)も実際そうであるように、その形は確率(予測分布関数)のかけ算になります。かけ算した関数は微分してその「勾配」を求めるのも一苦労です。
「かけ算した形になる」ことがあらかじめわかっているなら、対数を取って足し算に変えてしまいましょう。都合のいいことに対数は単調増加関数なので、対数をとっても大小関係は変化しない、つまり最小点(または最大点)は変わらないことが保証されます。
ところで「(または最大点)」といちいち但し書きをするのはめんどくさいですよね。
実は「最適化」と特に断りなく言った場合は最小化を指すことが多いです。最大化したい尤度関数も符号を反転しておけば、最小化で考えることができます。
その2つをあわせて、最尤推定の一般的なアプローチは「負の対数尤度関数の最適化」になります。
ロジスティック回帰モデルの負の対数尤度関数は次のようになります。
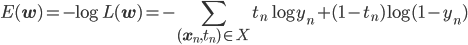
目的関数が足し算になりました。これなら勾配も求めやすそうです。
次回は実際に勾配を計算して、確率的勾配降下法の更新式を導出してみましょう。