技術的負債の「見える化」

どのようなソフトウェアにも設計上のミスはあります。設計時点ではサービスの発展性や日々変わりゆく要件を完全に予測することはできないからです。ある時点で正しい設計も，その次のサービスリリースでは設計上の修正を必要とするかもしれません。これらの変更への粘着性や複雑性のある状態を，「⁠技術的負債」と言います。

mixiでは技術的負債は長らく，コードレビューや技術力の高いエンジニアによる新機能リリース時の修正などで対応を行ってきました。しかし，これまでに紹介した「わかりやすいコードの指針」や「アーキテクチャパターン」をレビューや教育だけで維持することは，ソフトウェアが巨大になり，開発者数が増加するにつれて難しくなります。そのため現在では，ソフトウェアの設計品質評価を自動化するツール群を開発し，それらを用いて技術的負債を見える化し，計画的に解消していく試みを行っています。

コンポーネント内の負債指数

コンポーネント内部の負債の評価には，クラスの作りの問題を評価する「単一責務の違反指数」と，関数の作りを評価する「循環的複雑度」を用いて計算します。

クラスの単一責務の違反指数

先ほど，オブジェクト指向設計の重要な指針として単一責務原則を紹介しました。これを満たしているかを機械的に推計する方法として，mixiではバージョン管理システムの修正ログを利用する方法を採用しました。

具体的には，svn blame（指定したファイルの変更者とリビジョン情報を表示する）の実行結果から，次のような式で単一責務性の違反指数（SRP）を計算するようにしています。

• SRP＝R＋U＋((L/100)－5)

• R：修正リビジョンのユニーク数
• U：修正ユーザのユニーク数
• L：モジュールのライン数

この値が大きければ大きいほど単一の「大きな」モジュールが「何度も多くの人に」触られている状態であると言えます。これはコンポーネントの変更の多さに対してモジュールの分割が不十分であることを証明しているという判断によるものです。

この指標を各コンポーネント内のコードに適用し，降順に並べ替えると，「⁠王様モジュール」のようになっているものを割り出せます。

バージョン管理システムを利用していれば簡単なスクリプトで計算できるので，みなさんもぜひ利用してみてください。

関数の循環的複雑度

次に，関数の簡潔さ／複雑さを測定するにはどのようにしたらよいでしょうか。簡潔に記述された関数は，十分な命名と抽象化がなされていることが多く，読みやすく改修しやすいものになります。関数の簡潔さ／複雑さを測定する指標の一つに，ロジックの循環的複雑度（Cyclomatic Complexity）というものがあります。

まず単一の関数の循環的複雑度（M）は，次の式によって得られます。

• M＝E－N＋2P

• E：グラフのエッジ（関数内の処理のブロックをつなぐ線）数
• N：グラフのノード（関数内の処理のブロック）数
• P：連結されたグラフの数

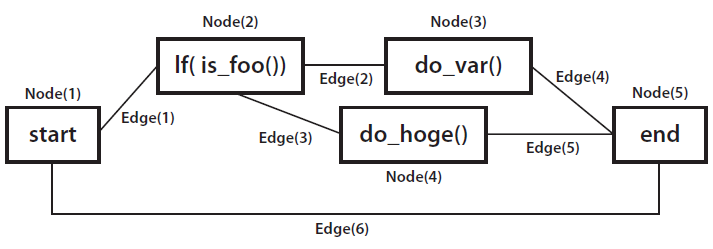
たとえば次のような関数があるとします。

do_one();
if( is_foo() ) {
    do_var();
} else {
    do_hoge();
}
do_moga();

この関数は図2のようなグラフ構造を描きます。ここから，この関数の循環的複雑度は6－5＋2×1＝3であると求められます。この値は分岐網羅率を達成するのに必要なテストケース数の上限を表します。この数が大きいほど完全なテストを記述するのが難しくなります。関数ごとの循環的複雑度は，Perl::Metrics::SimpleというCPANモジュールを利用すれば簡単に得ることができます。

そこからあるコンポーネント全体の循環的複雑度（CC）は，次のように求めています。

CC = sum map{ $_ -20 }
        grep {$_ > 20 }
            @method_complexities;

20は，テストが困難になったり，修正に弱くなるとされている関数の循環的複雑度（M）の値です。@method_complexitiesは，コンポーネント中のすべての関数ごとの循環的複雑度（M）です。上記コードでは，20からはみ出した数の合計をコンポーネントの循環的複雑度としています。この値が大きければ大きいほど，負債度の高いコンポーネントとみなすことができます。

コンポーネント内の負債指数の計算

単一責務の違反指数や関数の循環的複雑性の高さは，同一コンポーネント内の修正や機能追加の困難さを意味しています。これら2つを総合して評価するために，次のような式であるコンポーネント内の負債指数（P）を計算しています。

• P＝SRP×CC＋(SRP＋CC)

このスコアは，プロダクト内の修正すべきモジュールや関数の多さ，テストの困難さなどを反映しています。複雑なプロダクトや機能追加，変更の多いプロダクトほど高いスコアになりがちです。それだけリファクタリングに工数を割くべきであるため，コンポーネント内の評価として適切な役割を果たすことができます。