はじめに
データベースを扱う仕事をしていると、パフォーマンスの問題に悩まされることは日常茶飯事です。とくに最近は、データベースに格納されるデータ量が飛躍的に増え、サーバのCPUやメモリといったハード面の増強だけでは追いつかないことも多くあります。
そのようなケースに対応するため、DBMSは性能改善のための手段を多く用意しています。その中で最もコストパフォーマンスの良い方法が、インデックス(索引)です。アプリケーションにもハード構成にも影響を与えずに実行でき、うまくいかなければすぐに削除できるという手軽さが大きな魅力で、効果はしばしば絶大です。
インデックスにはいろいろな種類があり、またDBMSによってもサポートする種類に差がありますが、本稿では最も重要な2つを取り上げます。それが、B-treeとハッシュです。インデックスには、ほかにもビットマップインデックスや関数インデックスなどのバリエーションがありますが、ほとんど使わないか、上の2つの応用で理解できるものばかりです。
そのため本稿では、とくに重要な上記2つのインデックスについて、内部ロジックを解説し、それぞれどのような利点と欠点を持つのかを明らかにしていきたいと思います。また、ハッシュの場合はインデックスに限らず、ハッシュパーティションなど一般的なハッシュの使用法についても同時に説明します。
読者対象
実務でインデックスを使ったことのある人、または使いたいと考えている人
DBのパフォーマンス問題を抱えている人
稼働環境
B-tree
概要
特に一般的で重要な索引の種類は、B木(B-tree)である。すべてのアプリケーションに最適な単一の記憶構造というものが存在しないことは事実であるが、もし一つの構造が選ばれなければならないとすれば、B木の類が恐らく選択されていることはまず疑いようがない。
Christopher J. Date『データベースシステム概論』 第6版/丸善
インデックスというのは、( x,α)という形式の配列です。PerlやRubyをよく使う人には連想配列 と言ったほうがわかりやすいでしょうか。ここで、xはキー値、αはそれに結び付く情報..実データか、あるいはそれへのポインタ..です。実際には、DBにおいてαはデータへのポインタであることが多いため、C言語的な表現を使って、キー値とポインタの配列 と言っても良いでしょう。本の最後にあるインデックスも、キーとなる単語と、ページ番号(ポインタ)の連想配列です。
B-treeは、インデックスの中では一番ポピュラーで、日常業務で使うインデックスの90%はこれです。そのため、何の修飾もなしにCREATE INDEX文を実行すると、ほとんどのDBでは、暗黙にB-treeインデックスが作成されるぐらいです。
しかし誤解のないように言っておくと、B-Treeは、検索のアルゴリズムとしては飛び抜けて性能の良いものではありません。考案者の1人であるRudolf Bayer自身が「もし世界が完全に静的で、データが変化しないなら、ほかのインデックス技術でも同程度のパフォーマンスは達成できるだろう」と認めています。
長所
B-treeの長所は平均点の高さです。Dateの言葉を借りるなら、B-treeは「幅広い名手」なのです。B-treeに多角的な評価を付けると、次のように「オール4」の秀才型になります(図1 ) 。
❶均一性(4点) :各キー値の間で検索速度にバラツキが少ない
❷持続性(4点) :データ量の増加に比してパフォーマンス低下が少ない
❸処理汎用性(4点) :検索/挿入/更新/削除のいずれの処理もそこそこ速い
❹非等値性(4点) :等号(=)に限らず、不等号(<、>、<=、>=)を使ってもそこそこ速い
❺親ソート性(4点) :GROUP BY、ORDER BY、COUNT/MAX/MINなどソートが必要な処理を高速化できる
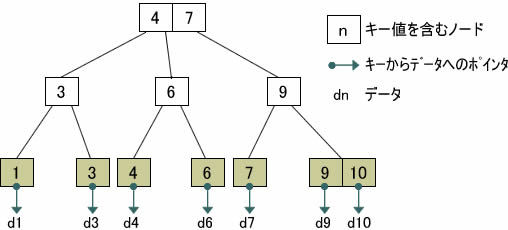
図1 B-treeの評価レーダーチャートB-treeがバランスよく高得点を取れる理由は、その構造を見るとわかります。今、整数値(1, 3, 4, 6, 7, 9,10)を含む列にインデックスを作成したとすると、図2 のような木が作られます。
図2 B+treeの構造最下層のリーフ(葉)と呼ばれるノードから、実データに対するポインタが出ています。なお、実際には多くのデータベースでは、リーフにだけキー値を保持するB+tree という亜種を採用しています(Oracle、Postgre SQL、My SQLなど) 。これは、B-treeに比べて検索をより効率的にしたアルゴリズムで、データベース以外でも、NTFSやXFSなどのファイルシステムでも利用されています。本質的な特徴はB-treeと変わらないため、以下、基本的にこのB+treeを前提に話を進めます。
COLUMN 3つの「B」
ちょっとトリビアな話ですが、B-treeの「B」が何の意味かはわかっていません。考案者のRudolf BayerとEdward M. McCreightが明かしていないからです。BalancedとかBroadという説が有力ですが、中にはBoeingという珍説まであります(Bayer がBoeing社の研究所に勤めていたため) 。
ただし、ときどき勘違いされているようにBinarytree(2分木)のBではありません。2分木は、1 つのノードがちょうど2つだけの子ノードを持つような木の名前ですが、B-treeのノードは3つ以上の子ノードを持つことができるからです(しかも、B-treeの2分木版として、Binary B-treeというのがちゃんと存在します) 。
特性
均一性
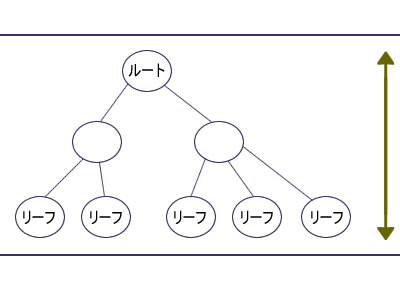
B-treeは、かなり特徴的な形をした木です。まず、どのリーフもルートからの距離(高さ)が一定です(図3 ) 。これは平衡木 (balanced tree )と呼ばれる木の特徴です。とくにB+treeはリーフにしかキー値を持たないので、探索に必要な読み込みブロック数(計算量はほぼこれで決まる)は、木の高さによって決まります。すると、リーフまでの距離が一定ということは、どのキーを使っても探索を同じ計算量で行えるということですから、検索や更新にかかる時間がキー値によらず一定 になるのです。
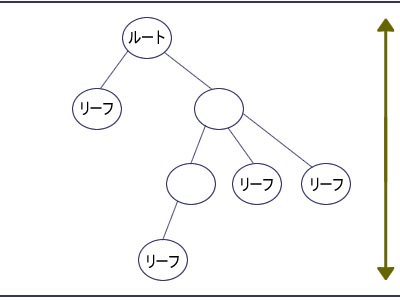
図3 平衡木:ルートからすべてのリーフまでの距離が同じ仮に、インデックスが非平衡木だったとしたらどうでしょう(図4 ) 。たとえば、5というキーを持つリーフの高さが3で、100というキーを持つリーフまでの高さが30だとすれば、WHERE句で条件に100を指定するクエリは、5を指定するクエリより10倍多くの時間がかかってしまいます。このように、同じ構造のクエリなのに指定する条件値によって応答時間にガタツキが生じるのは、システムのサービスレベルを維持するうえで大きな不確定要因になります。一方、B-treeインデックスでは、どちらのクエリもほぼ同じ時間で処理できます(リスト1 ) 。
図4 非平衡木:ルートからリーフまでの距離がバラバラリスト1 B-treeインデックスは、どちらのクエリもほぼ同じ時間で処理する SELECT *
FROM TestTbl
WHERE indexed_col = 5;
SELECT *
FROM TestTbl
WHERE indexed_col = 100;普通、木に対して挿入、削除など更新処理が繰り返されると、平衡木はバランスを失い、非平衡な木になってしまいますが、B-treeの場合、これを自動的に修復してバランスを保つアルゴリズムが組み込まれています。そのためB-treeは自己組織的な構造の一種でもあります。
持続性
B-treeの第2の特徴は、非常に「平べったい(broad) 」木、言い方を変えると、背の低い木だということです。背が低い、という主観的な表現で恐縮ですが、Bayerによれば、典型的なB-treeの高さは3~5です。これはデータ量が何百万、何千万行となっても変わりません[1] 。
平べったい形をしていることのメリットは、データ量が増えても検索や更新にかかる時間がほとんど増えないことです。先ほども述べたように、B-treeの検索に必要なディスク読み込みブロック数は、木の高さによって決まります。ということは、B-treeの場合、最悪のシナリオでも、まず4~5回のディスクアクセスで済んでしまうのです。
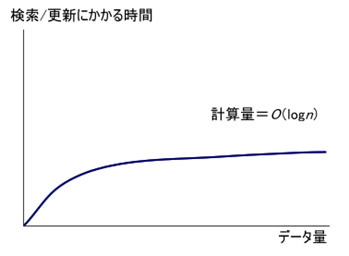
もう少し厳密に言うと、B-treeの検索と更新にかかる時間は、データ量に対して対数関数的(logarithmic)です。聞き慣れない言葉かもしれませんが、よく変化量に対して増加量が非常に大きいことを、「 指数関数的」と表現します。対数は指数の反対で、増加のしかたが非常に緩やかであることを意味します[2] ( 図5 ) 。
図5 B-treeはデータ量の増加に対して性能劣化が緩やかただ、対数関数的といっても、厳密にそうというわけではなく、実際には挿入と削除を繰り返してインデックスの構造が崩れたりすると、多少のズレは生じます。したがってこれは、「 だいたい」対数関数的という程度の目安だと思ってください。こういう大雑把な計算量を示すとき、ランダウの記号O で表現することがありますが、それを使えば、O (logn )となります(n はデータ量) 。
処理汎用性
ビットマップインデックスのようなインデックスは、検索速度は時にB-treeを凌駕しますが、更新処理に多大な時間がかかるという欠点を持ちます。しかし、B-treeの場合、挿入/更新/削除のコストも、検索と同じくデータ量n に対してO (logn )であるため、いずれの処理も「まあまあ」速く、かつデータ量が増えてもパフォーマンスがほとんど悪化しません。
非等値性
B-treeは、構築されるとき必ずキー値をソートします(文字型などの列でも、アルファベット順とか適当な順序でソートします) 。したがって、たとえばWHERE句で「100以上」という条件を指定した場合、まずはキー値=100のリーフを探し(これは平均3~4回のアクセスで見つかる) 、それ以降のリーフ全部を読み込むことで、条件に合致するキー値を漏れなく選択できます。
これによって、B-treeは、等号だけでなく、不等号やBETWEENを使った条件に対しても高速な検索が可能です(リスト2 ) 。これは、あとで紹介するハッシュにはない利点です。
リスト2 B-treeは不等号や範囲検索もそこそこ速いSELECT *
FROM TestTbl
WHERE indexed_col > 100;
SELECT *
FROM TestTbl
WHERE indexed_col <= 100;
SELECT *
FROM TestTbl
WHERE indexed_col BETWEEN 10 AND 100;ただそうは言ってもやはり、不等号の検索は、等号の検索に比べれば遅いですし、また、否定条件(<>、!=)に対しては、B-treeはまるで役に立ちません。また一般的に、B-treeはNULLをキー値として保持しないため、IS [NOT] NULLを指定した場合もインデックスは使われません(リスト3 ) 。
リスト3 否定条件やIS NULLでは役に立たない
SELECT *
FROM TestTbl
WHERE indexed_col <> 100;
SELECT *
FROM TestTbl
WHERE indexed_col IS NULL; 親ソート性
遅いSQL文によくありがちなパターンとして、巨大なソートをしている場合があります。SQLは明示的にソートを記述することはしませんが、次のような処理を記述したとき、内部でソートを行います。
集約関数(COUNT、SUM、AVG、MAX、MIN)
ORDER BY句
集合演算(UNION、INTERSECT、EXCEPT)
OLAP関数(RANK、ROW_NUMBERなど)
ソートがメモリ上で行われている間はそれほど大きなパフォーマンス低下は引き起こさないのですが、データ量が膨大でメモリ上には収まりきらない場合、データベースはしかたなく、ディスクへデータを書き出すディスクソートを行います。これが発生すると、ガクンとSQLのパフォーマンスが落ちます。そのため、ディスクソートはハイパフォーマンスを要求されるシステムにとって鬼門の1つです。
しかし、B-treeインデックスの存在する列をGROUPBY句やORDER BY句のキーとして指定することで、ソート負荷を軽減することが可能になるのです(リスト4 ) 。これは複数の列にインデックスを作成する複合インデックスの場合にも当てはまります。
リスト4 B-treeインデックスが高速化することがある処理の例
SELECT SUM(col)
FROM TestTbl
GROUP BY indexed_col;
SELECT indexed_col
FROM TestTbl
ORDER BY indexed_col;
SELECT COUNT (*)
FROM TestTbl;
SELECT MAX (indexed_col)
FROM TestTbl;
SELECT MIN (indexed_col)
FROM TestTbl;