「いろいろ学んだけど浅い気がする」という不安の声をよく聞きます。よく観察していると、この悩みには2通りのタイプがあります。「深い理解」軸の知識が足りていないタイプと、「抽象化」フェーズのやり方に慣れていないタイプです。
自分の知識が浅い気がする原因
「深い理解」方向の知識が足りない
一つは、ある程度経験を積んだプログラマによく見られるものです。いろいろなことを学んで、それを応用して成果も出している、なのになんだか不安、というものです。
このタイプの人は、自分の中では抽象化を行ってモデルを作ることができているのですが、その理解に名前が付いていません。そのため、自分で気付けなかったり、他人に説明できなかったりします。また、そのモデルが世間でどう呼ばれているのかを知らないため、本当は理解できているのにそのモデルについての会話についていくことができず、「自分は理解できていない」と感じてしまいます。
この症状は「深い理解」軸の語彙(ごい)が足りていないことが原因です。意識して「深い理解」軸の知識収集を行うことが必要です。そうすると「あー、それMediatorパターンって名前が付いてるのか! 知らずに使ってた!」とか、「あー、なんか言語によって違いがあるなーと思ってたけど、『静的型付け』と『動的型付け』の違いだったのか!」というように理解が整理されます。
「抽象化のフェーズ」に慣れていない
もう一つは、「抽象化のフェーズ」に慣れていないタイプです。抽象化のフェーズでは、自分でモデルを生み出さなければいけません。しかし「正解のモデルが本に書いてあって、それを見つけて読めばよい」と勘違いをして、片っ端から本を読んだりと「情報収集のフェーズ」ばかりを行ってしまいます。情報収集にはゴールがないので、いくら情報収集を繰り返しても不安が解消されません。
不安を解消し、自信を持つには、学んだことを成果につなげる必要があります。「情報収集」だけでは成果は出せません。得た知識を自分の中で「抽象化」してモデルにし、自分の問題に応用して、はじめて成果が出ます。
なぜ抽象化が必要?
なぜ抽象化が必要なのでしょうか。高校数学の問題を解くときのことを考えてみましょう。ある問題Q1を読んで、あなたは解き方がわからなかったとします。しかたがないので解答A1を読み、理解できて、Q1は解けるようになったとしましょう。では、よく似た問題Q2をあなたは解けるでしょうか? 解けないかもしれません。しかし、似た問題をいくつも解いているうちに、この種の問題の「解き方」をあなたは体得します。そうすると、類似の問題Q3がテストに出たときに、あなたは正解できるわけです。
このたとえ話で、A1を丸暗記していても、Q3を解けるとは限りません。A1は「抽象化されていない具体的な知識」だからです。一方「解き方」を理解したあなたは、Q3を解くことができます。「解き方」は、より一般的な対象に応用できる知識だからです。抽象化によって応用範囲が広がります。抽象化は一般化・汎用化なのです。
帰納による抽象化
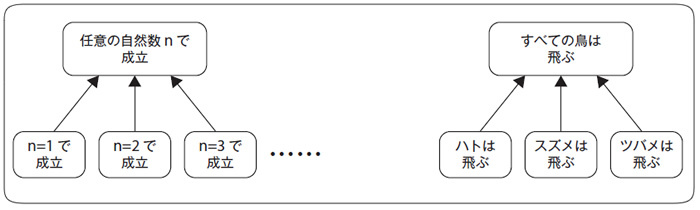
高校までの数学では、「一般的な知識」を「具体的な問題」に応用して「具体的な答え」を出すことが多く、その「一般的な知識」をどうやって作るかについてはあまり時間が割かれていないように思います。抽象化・一般化は帰納によって行われます。たとえば数学的帰納法では、n=1のときに命題Xが成立することを示し、n=2のときにもXが成立することを示し……と任意の自然数で成り立つことを示すことで、「任意の自然数kについてXが成り立つ」という一般的な知識を導きます(図1・注1)。
図1 左:数学的帰納法 右:帰納法
間違えてでも抽象化するメリット
みなさんは、普段の生活ではここまで厳密な証明をしていないことでしょう。かわりに、2~3個の事例を見てそこから帰納をしています。たとえばQ1とQ2の解き方から「この手の問題はこうすれば解ける」と考えたり、ハトやスズメやツバメが飛ぶことから「鳥は飛ぶものだ」と考えたりします。こうやって作られる抽象的な知識は、間違っていることもあります。たとえば、鳥類でもペンギンは飛ばないですね。
しかし、たとえ間違えてでも抽象化は必要です。抽象化をしないと、ウグイスを見たときに「ウグイスが飛ぶかどうかはわからない」と考えることになります。論理的には正しくても、実用的にはどうでしょうか。間違えることのコストが低い場合には、間違えるリスクよりも抽象化によって得られるメリットのほうが大きいでしょう[2]。
第1章では、Windowsにもlsがあるという間違いの例を見ました。間違えたことで、何か大きな問題があったでしょうか? むしろ学びのきっかけになったのではないでしょうか?[3]
どうやって抽象化するか
抽象化の確率を高めるツール
抽象化はどうすればできるのでしょうか。これは難しい問題です。正直なところ、「確実に抽象化を行う方法」はまだ知られていません。「情報を集めて、それからヒラメキを待つ」といった運頼みの方法しかありません。しかし同じ運頼みでも、確率が高まるとされる方法は、KJ法[4]、思考関連図[5]、グラウンデッド・セオリー[6]などいくつか考案されています。これらの方法の共通点を簡単にまとめると次の3点になります。
- 情報をたくさん収集する
- 情報を一覧できるようにする
- 関連のありそうなものを見つけて集め、ボトムアップで構造を作る
何がモデルを作るために有益な情報であるかは、モデルを得る前に知ることはできません。そこで、まず関係あるかもしれない情報をたくさん収集します。これが最初の一歩です。
人間が頭で考える場合、同時に検討できることはあまり多くありません。一方、ふせんに書き出して机の上に並べれば、100個ぐらいは同時に扱うことができます。机という「仮想記憶」を使うことで、人間の認知能力を底上げするわけです。
100枚のふせんを整理する際に、ボトムアップで構造を作ることはなぜ大事なのでしょうか。トップダウンで分類してしまう間違いがよくあるのですが、それは「すでに脳内にあるモデル」に合わせてふせんを並べているだけです。この作業の目的は「モデルを作ること」つまり「未知の構造を発見すること」です。ボトムアップでまとめていく過程で、予期しない構造を発見することが目的なのです。トップダウンで分類するとこのチャンスを失ってしまいます[7]。
筆者は2013年に『コーディングを支える技術』(注8)という本を書いたのですが、このときにKJ法がとても役に立ちました。1,000枚以上のふせんを作り、それをボトムアップで構造化し、その結果としてこの本があるわけです。
今回、KJ法について詳しく解説するには誌面が足りません。2013年夏に筆者が「京都大学サマーデザインスクール」で行った講義資料が公開されていますので、そちらを参考にしてください[9]。
比較から学ぶ
どういう知識を収集すれば、ボトムアップで理解を組み上げやすいでしょうか?
まずは比較です。たとえば、同じ目的についての異なる著者の本を数冊、比較しながら読むことです[10]。これによって「何が共通なのか?」「何が人によって意見の異なることなのか?」がわかります。
プログラミング言語を学ぶならば、自分の得意な言語とそうでない言語を比較することです。共通点もたくさんあります。一方で、異なる点もたくさんあります。「なぜ共通なのか?」「なぜ異なる選択を取ったのか?」これを考えることで理解が深まります。
ある分野での構造を、異なる分野での構造でたとえること(アナロジー)も、共通構造を見出すうえでの良い訓練になります。良いアナロジーを作ることができることと、対象をよく理解していることには相関があるように思います。
歴史から学ぶ
歴史から学ぶのは、今と昔の比較です。たとえば、過去の事例の中に、現在進行中の出来事と似た構造のものがあるかもしれません。共通点を見つけることで、よくあるパターンを学習できます。また、変更前と変更後の比較で、違いを見つけることもあるでしょう。何が変わったのか、どう変わったのか、なぜ変わったのか。これを考えることで理解が深まります。
特にソフトウェアでは、ソースコードを読めばなんでもわかるという勘違いをする人もいます。しかし、ソースコードには基本的に「今」の「how」の情報しかありません。「変更前にどういう問題があったのか」という「過去」の情報や、「なぜ変更する必要があったのか」「なぜこの選択肢を選んだか」という「why」の情報はソースコードからはわかりません。
そのような情報は、コミットログや開発者のメーリングリストでのやりとり、「Python Enhancement Proposal」のような議論のまとめなどに記述されています。意識して「why」を学ぶことが有益です。
抽象から学ぶ
「抽象的な知識を得るためには、抽象的なことを書いてある本を読めばよい」──こう言うと当たり前のように聞こえるかもしれません。これが最短経路のように思えるかもしれません。でも、これは危険な道です。
本章の冒頭で紹介したように、すでに経験を積み、具体的な知識をたくさん持っている人にとっては、この種の本を読むことで「自分の経験」を構造化する助けになります。一方で、具体的な知識をあまり持たない場合、第1章で見たような「応用できない知識」になってしまいます。次の3点に注意してみましょう。
- 自分の言葉で説明できるか?
- 自分の経験に基づいた具体例を挙げることができるか?
- 自分の目的を達成するためにその知識を使えるか?
こういうことができないのだとすると、本当はわかっていないのにわかったような気になっているだけかもしれません。自分がわかっているのかわかっていないのかを検証することが必要です。そこで次の「作って学ぶ」が重要になります。
作って学ぶ
「作って学ぶ」は理解の検証です。実際に手を動かして作ってみることで、自分が何をわかっていないかを知ることができます。
試してみて結果が期待どおりかを検証する
本を読んだり勉強会で話を聞いて「なるほど、わかった」と思ったとします。その「わかった」という感覚は、本当に正しいのでしょうか?「わかった」は「仮説」であり、「検証」が必要です。検証のためには、自分の理解をもとに行動をして、その結果が自分の期待どおりであるかどうかをチェックする必要があります[11]。
モデルが修正されるサイクル
第1章では学びに3つのフェーズがあるという話をし、「Windowsでls」という例を挙げました。とても小さな例ですが、これはうまくサイクルが回った例です。「すべてのOSでlsができる」という理解に基づいて行動し、その結果が失敗することで「自分が何を知らないか」に気づくことができました。
もう一つ例を紹介します(図2)。「Aを作りたい」と思ったときに、まず「どうすれば作れるか?」(how)を考えることでしょう。脳内のモデルが「BとCを組み合わせればできるはず」と答えたとしましょう。これは仮説です。実際にそのとおりに作ってみて、仮に失敗してAではなくDができてしまったとしましょう。あなたは「BとCを組み合わせるとDができる」という新しい知識を手に入れました。
図2 実行し、結果を検証し、モデルが修正されるサイクル
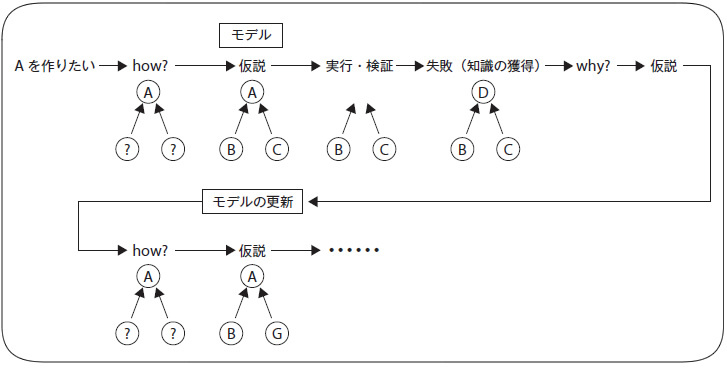
次に「なぜそうなったのか?」(why)を考えることでしょう。その結果「これが原因ではないか」という仮説を思い付きます。これはモデルの修正案です。
あなたは仮にこの修正案を受け入れてモデルを更新し、新しいモデルでAを作る方法(how)を考えます。そしてCではなくGを使えばAを作れるのではないか、と思いつきます。そして以下同様のサイクルが繰り返されます。
作るものを高度にしすぎない
「作って学ぶ」と言うと、ついつい「自慢できるようなゲームを作る」だとか「賞賛されるようなすごいサービスを作る」を目標にしてしまう人も多いかと思います。その目標でやる気が出ているのならそれでもかまいません。しかしやる気が出ていないのだとすると、その原因の一つは「目標が遠すぎる」ことでしょう。第2章でも解説したとおり、もっと細かい単位に分割しましょう。
作るものはプログラムとは限りません。たとえば何か新しいことを学んだのなら「まだ知らない人、1日前の自分に説明するとしたら、どう説明するか?」を考えてブログ記事を書くのも「作る」です。説明しようとすると自分の理解のあいまいなところがわかります。
学んだことを勉強会で発表するのもお勧めです。発表しながら観客の顔色を見て、もしポカンとしていたのなら、うまく説明できていないということです。質問が盛り上がらなかったら、見当違いな質問が来たら、それもうまく説明できていないということです。次回はもっとうまく説明できるように、改善のサイクルを回すことで理解が深まります。
プログラミングは検証がしやすい
とはいえ、プログラミングにはすごく良い特徴があります。他人の手を借りずに検証のサイクルを回せることです。プログラムを書いて実行すると、たとえばコンパイラが「何行目がおかしい」と怒ってくれます。実行結果が期待と違う出力になってしまったら、ステップ実行してどこまでが期待どおりの挙動かを確かめることができます。これは失敗の原因を突き止めるうえでとても楽です。他人の反応を待つことなく、1人で実験と検証のサイクルを高速に回すことができます。
もしあなたがミュージシャンだったら、曲を作って演奏し、反響を見るまでにどれくらいの時間がかかることでしょう。他人の反響から何が失敗の原因だったかを突き止めることができるでしょうか。
プログラマは理解を深めるうえでとても恵まれた環境にいるわけです。これを活かさないのはもったいないことです。
おわりに
本章では、知識の抽象化について学びました。抽象化によって得られるモデルは、必ずしも正しくありません。正しくなくても、モデルがないよりはマシなのです。モデルがあれば、答えを知らない問題に対しても自分なりの答えを出すことができるようになります。
モデルが正しいかどうかは、モデルに従って行動し、その結果が期待どおりかを確認することで検証します。この検証を繰り返すことで、徐々にモデルが改善されていくのです。
どうやって抽象化するかという方法論には、まだまだ改善の余地があるように感じています。個人の抽象化能力を何らかの方法で鍛えられないか? 抽象化の過程をうまく言語化できないか? 抽象化を助ける道具を作ることができないか?
筆者は、コンピュータが人間の抽象化フェーズを支援する方法や、人間に頼らずにコンピュータ自身が抽象化フェーズを行う方法に興味があり、今後も研究を続けていきたいと思っています。




