概要
微分積分は中学から高校へ,また高校から大学へと進んだときに,その扱う内容の抽象度に差があり苦手意識を持つ人が出てしまう科目の筆頭です。しかし,実は小学校で学んだ速度や濃度など算数の領域にすでに微分積分の核心はあったのです。本書の第1部ではまずその辺から最小限の数式だけを使って説明し,微分積分の考え方を見直していきます。第2部では,第1部で理解した考え方がどういう意味を持ってくるのか,なんのために計算をしているのかを探っていきます。
こんな方におすすめ
目次
【本書の内容】
読者の皆様へ
<第1部 微分積分学の考え方>
第1章 微分学とはどういう数学か
第2章 微分積分学が扱う対象 関数
第3章 微分学の方法 極限の考え方
第4章 関数の微分
第5章 積分学とはどういう数学か
第6章 積分学の方法 分けて和をとる
第7章 微分と積分の関係 微分積分学の基本定理
<第2部 微分積分学の計算技法>
第8章 導関数の計算
第9章 極限を求める
第10章 関数のテイラー展開
第11章 原始関数の計算
第12章 積分を求める
終わりに
サポート
正誤表
本書の以下の部分に誤りがありました。ここに訂正するとともに,ご迷惑をおかけしたことを深くお詫び申し上げます。
(2017年11月21日最終更新)
P.87 下から8行目の式の右辺第3項
| 誤 |
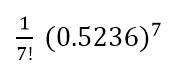
|
|---|
| 正 |
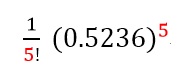
|
|---|