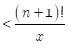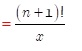概要
いまや統計学は必須科目になっています。本書は,大学で統計学の単位をとるための必携書です。社会人の方の学び直しにも最適です。手法だけではなくその理論的背景にも触れることで,理解しやすく,また応用力が付く構成となっています。解説はもちろん例題,問題に加え,要所要所で補足も細かく書き込んでいます。また,別冊として,演習問題,確認問題を用意しています。それにより確実に力をつけることができます。実際のデータを使って推測,検定も行っていますので,自分で試したいデータがあればやってみることもできます。統計学が楽しくなること間違いなしです。
こんな方におすすめ
- 大学で統計学を履修している学生,統計学初学者,社会人で統計学が必要な方々
目次
第1章 イントロ
第2章 確率分布
- 1 確率変数
- 2 離散型確率分布
- 3 連続型確率分布
- 4 累積分布関数
- 5 正規分布
- 6 正規分布の値
- 7 チェビシェフの不等式と大数の法則
- 8 2変数の離散型確率分布
- 9 X,Yの1次式の期待値・分散
- 10 2変数の連続型確率分布
- 11 確率変数の独立
- 12 確率変数の変換(partⅠ)
- 13 確率変数の変換(partⅡ)
- 14 積率母関数
- まとめ
第3章 推測統計
- 1 点推定
- 2 推測統計で用いる主な分布
- 3 区間推定
- 4 検定
- 5 母平均の差の検定
- 6 適合度検定・独立性の検定
サポート
ダウンロード
[別冊]問題演習の使い方
別冊から問題のみ(別冊から解答をはずしたもの)にしたPDFをダウンロードできます。
独習用としてご活用ください。
- [別冊]問題演習ダウンロード
- bessatsu_mondai_ensyu_toukeigaku.pdf
正誤表
本書の以下の部分に誤りがありました。ここに訂正するとともに,ご迷惑をおかけしたことを深くお詫び申し上げます。
P.45ページ 公式1.13の[証明]の上から4行目の式の一番左辺
| 誤 |
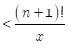
|
|---|
| 正 |
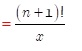
|
|---|
P.27 下から5行目
P.65 連続型確率分布(1変数)
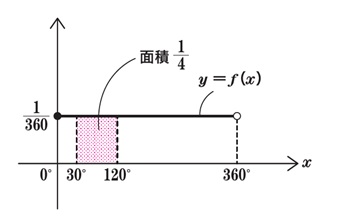
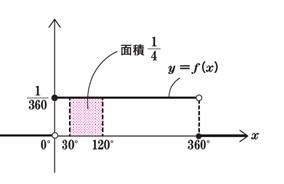
P.91 真ん中の図の右側
| 誤 |
|
|---|
| 正 |
|
|---|
f(x)=0(x<0, 360≦x)のグラフを追加
P.121 定理2.17 最後のkの条件
P.172 下から4行目
P.173 「■確率変数の和」の前,下から2行目
P.179 図の上のyの条件
| 誤 |
y≧0のとき、 x≦zy y≦0のとき、x≧zy
ですから、y≧0のときとy≦0のときに分けて積分すると
|
|---|
| 正 |
y>0のとき、x≦zy y<0のとき、x≧zy
ですから、y>0のときとy<0のときに分けて積分すると
|
|---|
P.186 ポップの枠の上から4行目
P.231 図の右上にあるコメント
P.244 上から12行目
| 誤 |
「正しいコインでないこと」
|
|---|
| 正 |
「正しいコインである」こと
|
|---|
P.277 上から4行目
P.61 一番上の式の2項目[ ]の中
| 誤 |
(x+1)log(x+1)-(x+1)
|
|---|
| 正 |
(x+1)log(x+1)-x
|
|---|