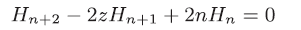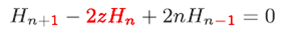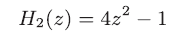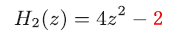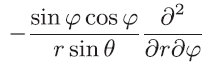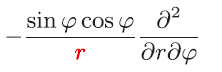概要
量子力学は,素粒子のようなミクロの世界で適用される理論です。身近な例では,携帯電話やゲーム機に使われている半導体の世界における考え方です。
本書は,天才物理学者たちが挑戦し謎ときをしてきた量子力学の基本的な考え方や発展経緯が初心者にもわかるように,図やイラストを豊富に使って解説した入門書です。重要な数式には詳しいコメントをつけて理解を助けるようにします。また章ごとにまとめをつけ,内容をすっきりと整理できるよう工夫してあります。難しい数式は巻末にまとめ,本文では限定した重要な数式だけで説明をします。現代物理学のとても面白い世界を堪能することができます。
こんな方におすすめ
- 量子力学に興味のある人
- 量子力学をやりなおしたい人
- シュレディンガー方程式に興味ある人
目次
第1章 量子力学までの道のり
- 1-1 ミクロの世界への探求
- 1-2 光は波?
- 1-3 光は粒子?
- 1-4 光の二重性
第2章 古典論から量子論へ
- 2-1 温度と色の関係(黒体輻射)
- 2-2 エネルギー量子説
- 2-3 水素原子の構造(ボーアの原子模型)
第3章 量子力学の原理
- 3-1 量子的イメージ
- 3-2 波束と不確定性関係
第4章 シュレディンガー方程式
- 4-1 波動関数とシュレディンガー方程式
- 4-2 固有値と固有関数
- 4-3 量子力学の数学的表現
第5章 無限に深い井戸型ポテンシャル
- 5-1 1次元井戸型ポテンシャル
- 5-2 立方体に閉じ込められた自由粒子
第6章 有限の深さの井戸型ポテンシャル
- 6-1 シュレディンガー方程式の立式
- 6-2 エネルギー固有値の導出方法
第7章 1次元散乱問題とトンネル効果
第8章 調和振動子
- 8-1 単振動
- 8-2 調和振動子の量子力学的特徴
第9章 中心力場ポテンシャルのシュレディンガー方程式
- 9-1 3次元球座標ラプラシアン
- 9-2 中心力場ポテンシャルのシュレディンガー方程式
第10章 角運動量の量子化
- 10-1 角運動量の定義
- 10-2 角運動量の量子化
第11章 水素原子
- 11-1 水素原子のシュレディンガー方程式
- 11-2 シュレディンガー方程式を解く
第12章 シュレディンガー方程式の近似解法
- 12-1 量子力学における摂動論
- 12-2 定常状態で縮退がない場合の摂動論
- 12-3 定常状態で縮退がある場合の摂動論
- 12-4 非定常状態の摂動論
第13章 さらに勉強したい人のために
- 13-1 角運動量の代数関係
- 13-2 スピン
- 13-3 粒子のスピンと統計性
サポート
正誤表
本書掲載の記述に誤りがありました。訂正するとともに,読者の皆様および関係者の方々に深くお詫び申し上げます。
第4刷への正誤表
P.112 図7-11中の平方根の中身
V_0の2乗が不要です。
第3刷への正誤表
P.125 中央の数式のうち2つ目の式
P.163 (11.3)式のすぐ下の文章
P.184 (12.15)式のすぐ上の文章
| 誤 |
…Ψ^(1)_mなので…
|
|---|
| 正 |
…Ψ^(0)_mなので…
|
|---|
P.192 上から2行目の文章内の式
| 誤 |
…+|V_n1,n2|…
|
|---|
| 正 |
…±|V_n1,n2|…
|
|---|
第2刷までへの正誤表
P.72 1行目
P.76 上から7行目 式(5.12)の手前の一文
P.94 下から5行目
P.102 1行目の「(水が湧き出ているとき、∂S/∂x=0)」
P.121 (8.22)の上式
| 誤 |
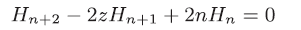
|
| 正 |
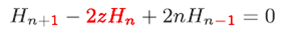
|
|---|
P.121 (8.25)3つ目の式
| 誤 |
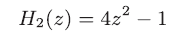
|
| 正 |
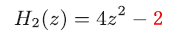
|
|---|
P.128 上から1行目
| 誤 |
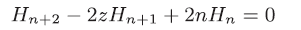
|
| 正 |
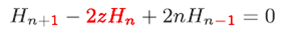
|
|---|
P.188 図12-3の中
P.235 上から7行目の第2項
| 誤 |
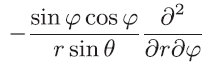
|
| 正 |
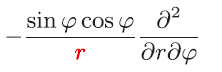
|
|---|
P.241 「○表示」の式
| 誤 |
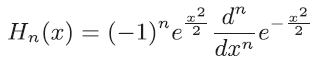
|
| 正 |
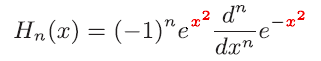
|
|---|
P.245 (A4.4)式
ダウンロード
本文使用の図版データ
(2024年4月26日更新)
本書をご購入いただいた方は,本書で紹介している図版データをダウンロードいただけます。以下の圧縮ファイルをダウンロードしていただき,適宜解凍してご利用ください。
なお,本書を用いた講義用のスライドにのみ使用を許諾しております。それ以外のデータの一部または全てを無断で複製・変更・使用することはできません。ご注意ください。
ご購入の証明として,以下に表示される本書内の特定箇所の文字列をキーワードとして入力してください。