概要

正多面体は，正四面体，正六面体，正八面体，正十二面体，正二十面体の５つしかないと言いますが，果たして本当でしょうか？ どうやって確かめるのでしょうか。
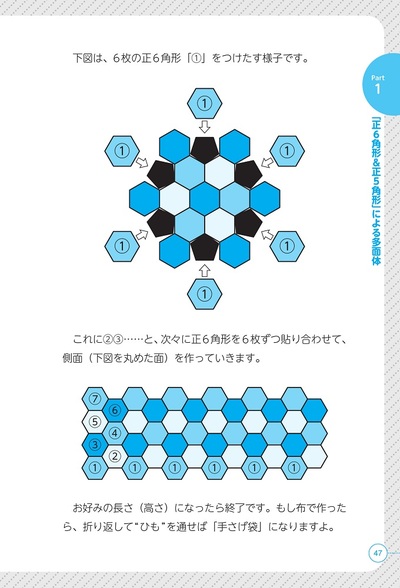
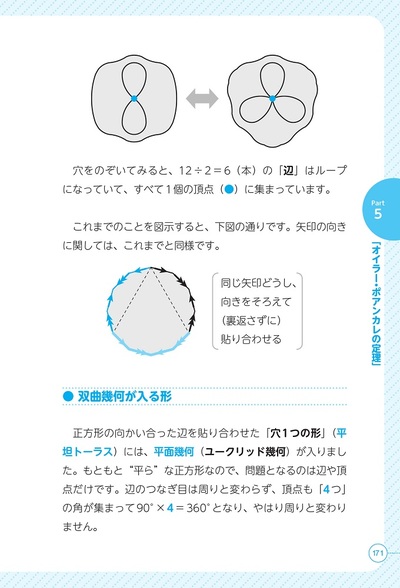
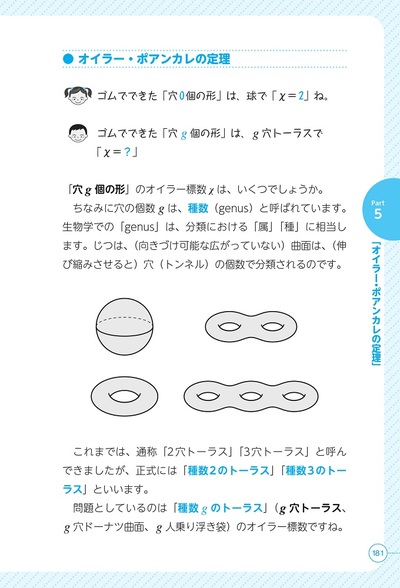
本書では，そもそも平面ってなに？ 曲がるの？ といった素朴な疑問から丁寧に解消していき，正多面体からやわらかい幾何であるトポロジーへと平面や立体の話題を自然につなげていきます。実は，1つ穴のトーラス，2つ穴のトーラスなどは正多面体ですべて説明がつくのです。身近にある紙などを使って実際に図形を作って試してみることもできるコラムも設けますので，楽しみながら多面体，その先にある非ユークリッドを学ぶことができます。

こんな方におすすめ

• 図形，幾何に興味がある人，三角形の内角の和は本当に180度？オイラーの多面体定理は本当に成立するの？といった疑問を持っている方々

サンプル

目次

• はじめに

Part1「 正6角形&正5角形」による多面体〜 「サッカーボール」から「フラーレン」へ 〜

• 1「 双対な多面体」で見る「サッカーボール」
• 2「 オイラーの多面体定理」で解く「フラーレンの“12”」
  • 工作コーナー 「 正6角形＆正5角形」で作る形
  • 塗り絵コーナー 文様「七宝つなぎ」と「麻の葉」

Part2「 正多面体」から「トーラス」へ〜 頂点周りが“平ら”な正多面体もどき 〜

• 3「 正方形」で作る“平ら”な正多面体もどき
• 4「 正6角形」で作る“平ら”な正多面体もどき
  • 工作コーナー 「 正方形＆ひし形」でパッチワーク
  • 塗り絵コーナー 「ひし形」を探そう！

Part3 「正多面体」から「g穴トーラス」へ〜 頂点周りが“だぶついた”正多面体もどき 〜

• 5「 窓3つの形」は「穴いくつの形」か？
• 6「 穴2つの形」は「窓3つの形」だけか？
  • 工作コーナー 正方形10枚で作る「穴2つの形」

Part4「双曲平面」上の「非ユークリッド幾何」〜「球面」「平面」「双曲平面」上をアリが歩くと 〜

• 7「 球もどき」が正多面体なら「双曲平面もどき」は？
• 8「 ポアンカレの円板モデル」で「非ユークリッド幾何」
  • 工作コーナー 「 アルキメデスタイル貼り」でパッチワーク
  • 塗り絵コーナー “非”アルキメデスタイル貼り

Part5「 オ イラー・ポアンカレの定理」〜「 オイラー標数」に現れる「穴の個数」 〜

• 9「穴g個の形」を正多角形“1枚”で！
• 10「 穴の個数」を「オイラー・ポアンカレの定理」で！
  • 工作コーナー 正6角形12枚で作る「穴4つの形」

• 索引
• 参考文献／著者プロフィール

サポート

現在サポート情報はありません。