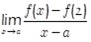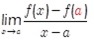目次
- まえがき
【入門編】 素数ほど面白い数はない
- 素数ってなに?なんで注目されるの?
- 数学者は素数が大好き
- 素数は不規則に出現する
- 素数の末尾はいくつ?
- 素数の末尾に偏りはあるの?
- 双子素数予想
- ゴールドバッハ予想
- メルセンヌ素数
- Column 素数魔法陣
【初段編】 なぜ,素数は無限にある?
- 素数は無限にある
- ユークリッド-マリン数列
- もう一つのユークリッド-マリン数列
- 4で割った余りでの分類
- 4n+3型素数が無限にある理由
- 4n+1型素数が無限にある理由
- 4n+1型素数と4n+3型素数は同じくらいある
【二段編】 数列の中の素数
- 素数を生み出す式
- 等差数列の中の素数
- 等差数列を成す素数
- 「素数による等差数列の定理」を証明しよう
- いくらでも長い「素数による等差数列」が存在する
- 2次式の数列の素数
- 指数関数で作られる数列
- リュカ-レーマーの判定法
- フェルマー数とフェルマー素数
- オイラーのアプローチ
- 素数を生成する多項式
【三段編】 対数関数と素数
- 対数関数と素数
- 底が2の対数関数
- 対数法則ってどんな法則?
- ネピア定数と自然対数
- 素数の個数を表す関数
- 偉大なる素数定理
- 素数定理は,どの程度の近似を実現するか?
- 素数の「出現確率」
- 素数を数えるチェビシェフ関数
- チェビシェフの不等式
- チェビシェフ第2関数と素数定理
- チェビシェフ関数定理の証明を直感的に理解する
- Column オイラーのフェルマー素数の約数発見法
【四段編】 合同式と素数とRSA暗号 ~フェルマーの小定理,オイラーの定理
- 数が社会で役立つ時代
- RSA暗号とはどんな暗号か
- フェルマーの小定理
- 擬素数
- オイラーの定理
- ウィルソンの定理
- 合同になじもう
- 合同式の操作は等式のものとほとんど同じ
- 定理たちを証明しよう
- オイラーの定理の証明
- ウィルソンの定理は,「逆数」と関係する
- RSA暗号を支える原理
- なぜ, 難攻不落の暗号なのか?
【五段編】 順列・組合せと素数 ~素数定理への最初のアプローチ
- 順列・組合せと素数は仲良し
- nCrの公式を理解する
- 2項定理
- 組合せ数からフェルマーの小定理へ
- nCrは特別な存在
- 2nCnの素因数を調べる
- 2nを割った商が奇数の素数
- 2nCnの近似素因数分解
- 組合せ数2nCnの素因数分解
- 2nCnの大きさをおおざっぱに見積もる
- いよいよ,素数定理のからくりを解明する
【六段編】 無限和と素数 ~オイラーの大発見
- オイラーの新発見
- 無限個の数を加え合わせる
- 有限になる無限和・無限になる無限和
- 無限和が教えてくれること
- エルデシュ分解
- 「オイラーの素数定理」を証明しよう
- 双子素数の逆数和
- エルデシュ分解のパワー
【七段編】 虚数と素数
- 不思議な数・虚数
- フェルマーの2平方定理
- 空想の楽園~複素数
- 2次元の数世界~複素数
- ガウス整数
- 2平方定理とガウス素数
- 平方剰余
- ガウス素数と平方剰余
- -1は平方剰余となる素数
- 2次体の整数論が花開く
【八段編】 素数と微分積分
- 微分積分は数学最強のツール
- 微積分は素数とも相性がいい
- 関数を局所的に見る
- 微分係数は接線の傾き
- 極値への応用
- 2次近似を利用する
- 微分係数とランダウ記号
- ランダウ記号を正式に定義しよう
- 微分係数は極限で求められる
- 多項式の微分係数
- テイラー展開と無次元の多項式
- 1次近似式を集計する
- 素数と積分の関係
【九段編】 ラマヌジャンとベルトラン=チェビシェフの定理 ~ψ(x)による証明
- ベルトラン予想
- 異色の天才ラマヌジャン
- チェビシェフ第1関数とチェビシェフ第2関数
- 証明のナビを見ておく
- 階乗数の素因数分解
- T(x)とψ(x)の関係を発見する
- T(x)の値を近似する
- チェビシェフ第2関数を評価する
- 証明を完成しよう
【A級編】複素数上の微分積分
- (A級その1)三角関数と複素数
- (A級その2)オイラーの公式
- (A級その3)指数が複素数のべき乗計算
- (A級その4)三角関数のテイラー展開
- (A級その5)複素関数としての対数関数
- (A級その6)複素関数の微分
- (A級その7)正則関数のテイラー展開
- (A級その8)複素べき乗関数の微分と「一般化された2項定理」
- (A級その9)複素関数の積分
- (A級その10)コーシーの積分定理
- (A級その11)コーシーの積分公式
- ガンマ関数
- (A級その12)ガンマ関数を解析接続する
【名人編】 ゼータ関数・リーマン予想・素数定理
- ゼータ関数は素数のすみか
- 有限ゼータ関数
- 関数等式とはどんな等式か
- 有限ゼータ関数ではオイラー積は当たり前
- 零点の分布
- バーゼル問題
- 無限個の因数分解
- 自然数s乗の逆数和の収束と発散
- 発散級数の和
- ゼータ関数と素数が結びつく
- オイラー積を応用する
- 天才リーマンの登場!
- 等差数列の中の素数~ディリクレの算術級数定理
- 発散級数を計算する解析接続
- リーマン・ゼータ関数の関数等式
- 難攻不落のリーマン予想
- 虚の零点はどのように分布しているか?
- 素数の個数をぴったり計算する式
- 明示公式から素数定理を証明する
- ペロンの公式
- 明示公式に到達しよう
- 素数名人の称号!
- あとがき
- 参考文献,かつ,お勧めの本
- 索引
- 著者略歴