概要
【2023年度 日本数学会出版賞 受賞】
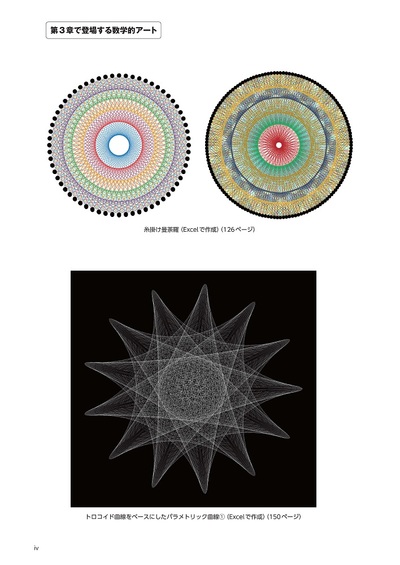
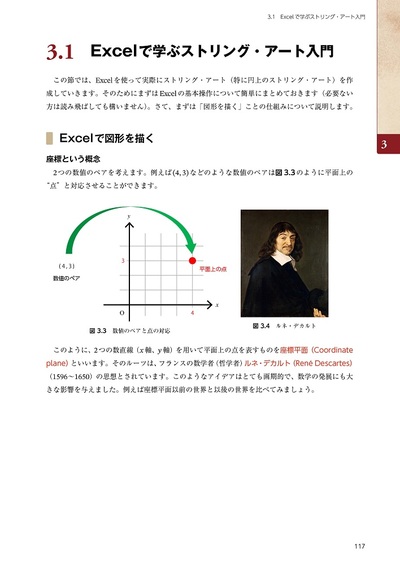
「数学はアート」ととらえ,「魅せる」数学をとことん追求したこれまでにない内容になっています。
まず,私達の身の回りにある折り紙の歴史から簡単に紹介します。折り紙は数学の幾何的な説明を理解するにはとっておきの題材です。数学の研究分野として「折り紙数理」が存在するほどです。実際に「折り紙を5等分できるか」「折りたたまれたときにできる折り線の特徴」「折り鶴の自由度」,ミウラ折りのきっかけやヨシムラパターンの解説などを行い体感,感動しながら読み進めることができます。
後半では,パターンや平面に敷き詰められた「模様」をご紹介します。折り紙はいわば「鏡反射」の幾何学です。平面タイル張りに関する数学(群論)によってエッシャーのタイル張りの模様をExcelで実際に描いていきます。切り絵では,数学的でかつ芸術的な世界を堪能できます。
そしてストリング・アートではExcelを使って,形を自由に変形して楽しむことができます。
驚くほど美しくきれいな図形が実はExcelで描けるのです。ちょっと数値を変えるだけで現れる目を見張るような美しいアートをぜひ実際に試してみてください。
こんな方におすすめ
- 数学を楽しみたい人,興味がある人,数式には抵抗があるけどなんとなく知りたいと思っている人,折り紙が好きな人
目次
第1章 黄金比の数理
- 1.1 黄金比とは
- 1.2 2次方程式と黄金比の歴史
- 1.3 貴金属比
- 1.4 五芒星と黄金比
- 1.5 黄金比が現れる問題
- 1.6 フィボナッチ数と黄金比
- 1.7 植物と黄金角
第2章 幾何学模様の数理
- 2.1 折り紙の歴史
- 2.2 折り紙と幾何学
- 2.3 折り紙と黄金比
- 2.4 平坦折り紙の理論
- 2.5 ミウラ折り
- 2.6 繰り返し模様の歴史
- 2.7 タイリングのする意
- 2.8 エッシャーと数学
- 2.9 非周期タイリング
第3章 ストリング・アートの世界
- 3.1 Excelで学ぶストリング・アート入門
- 3.2 螺旋のアート
- 3.3 エピサイクロイドとハイポサイクロイド
- 3.4 スピログラフとトロコイド曲線
- 3.5 リサージュ曲線
- 3.6 数列の描くストリング・アート
第4章 フラクタルとランダムのアート
- 4.1 フラクタル図形とは
- 4.2 フラクタルの歴史と数学
- 4.3 パスカルの三角形とフラクタル
- 4.4 ドラゴン曲線
- 4.5 乱数を使った「ランダム・アート」
- 4.6 力学系とカオス・アート
第5章 デザイン,アートへの活用例
- 5.1 Excelアートのデザイン活用例
- 5.2 数学と切り絵
サポート
正誤表
本書の以下の部分に誤りがありました。ここに訂正するとともに,ご迷惑をおかけしたことを深くお詫び申し上げます。
P.34 図1.39 「3か月」の写真の数
| 誤 |

|
|---|
| 正 |

|
|---|
「3か月」のところの画像の数は2枚。
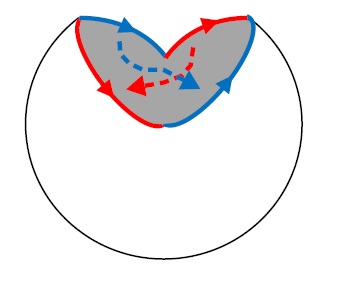
P.101 図2.73 真ん中
| 誤 |
|
|---|
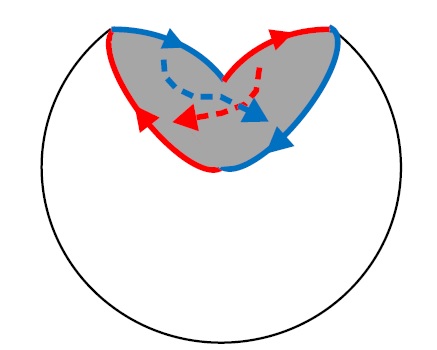
| 正 |
|
|---|
下の赤い矢印と青い矢印の向きが逆。
P.136 図3.35 の左上の吹き出しの式
| 誤 |
=COS(2*PI()*A2*$E$2/$F$2)
|
|---|
| 正 |
=B2*COS(2*PI()*A2*$E$2/$F$2)
|
|---|
P.136 図3.35 の右上の吹き出しの式
| 誤 |
=SIN(2*PI()*A2*$E$2/$F$2)
|
|---|
| 正 |
=B2*SIN(2*PI()*A2*$E$2/$F$2)
|
|---|