書籍概要

知の扉

測度の考え方
～測り測られることの数学～

著者
発売日
更新日

概要

「私たちは日常から長さや面積や体積を測っています。しかし，そもそも「測る」とはどういうことなのでしょうか。この「測る」ことを数学的に抽象化したものが測度です。本書では簡単な集合の解説から始めて，測れるもの，測ることができないものの性質を調べ，測度論とはいったい何をしているのかを易しく読み解いていきます。

こんな方におすすめ

  • 大学で測度論を勉強し始めた人
  • 測度論を学ぶ目的がいまいちピンとこない人
  • 集合とどう関係があるのかわからない人
  • 確率「測度」とのつながりがつかめない人など

サンプル

samplesamplesamplesamplesample

目次

  • まえがき

［第1部　測度論以前のこと］

第1章　長さ，面積，体積の昔

  • 1.1　測るということ
  • 1.2　どんな形でも測れるのか？
  • 1.3　円の面積はなぜπr2 か
  • 1.4　アルキメデスのとりつくし法
  • 1.5　錐体の体積はなぜ柱体の1/3 か

第2章　測り，測られることの数学的基礎1－集合

  • 2.1　始まりはいつも集合
    • 2.1.1　集合とはなにか？ －素朴な定義
    • 2.1.2　有限集合と無限集合
    • 2.1.3　無限集合の2つの種類
  • 2.2　「図形」を集合と見るには
    • 2.2.1　和集合と共通部分，「または」と「かつ」
    • 2.2.2　差集合と否定
    • 2.2.3　集合の分割と同値関係

第3章　測り，測られることの数学的基礎2－実数と写像

  • 3.1　測る「量」としての実数
    • 3.1.1　実数の区間と無限大
    • 3.1.2　実数の実感
    • 3.1.3　実数の連続性について
    • 3.1.4　上極限と下極限
  • 3.2　写像
    • 3.2.1　写像の基本
    • 3.2.2　簡単な写像の知識̶ 全射，単射，全単射，逆写像など
    • 3.2.3　ちょっと高度な写像の知識̶ 像と逆像，制限と拡張など
    • 3.2.4　関数と連続性

［第2部　具体から抽象へ－カラテオドリの条件のパズルとルベーグ測度］

第4章　基本図形で覆って測る：外測度の考え方

  • 4.1　外測度の考え方
    • 4.1.1　1次元にも複雑な図形がある
    • 4.1.2　複雑な図形をどう測るべきか
    • 4.1.3　「長さゼロ」とは？
    • 4.1.4　区間[0, 1] の外測度は1か？
  • 4.2　外測度の性質
    • 4.2.1　他の種類の区間の外測度と単調性
    • 4.2.2　平行移動不変性と加法性
    • 4.2.3　劣加法性

第5章　ルベーグ測度

  • 5.1　カラテオドリの条件とルベーグ可測集合
    • 5.1.1　加法性のパズル－ カラテオドリの条件
    • 5.1.2　カラテオドリの条件のパズル：条件の言い換え
    • 5.1.3　パズル2：基本的な図形が条件を満たすこと
    • 5.1.4　パズル3：集合演算が閉じていること
    • 5.1.5　パズル4：可算個の和集合が閉じていること
  • 5.2　ルベーグ測度
    • 5.2.1　ルベーグ外測度からルベーグ測度へ
    • 5.2.2　ルベーグ測度の性質
    • 5.2.3　外測度と測度の抽象化への道
    • 5.2.4　ルベーグ可測でない集合

［第3部　抽象から具体へ－測り測られることの本質を抜き出す］

第6章　定義で始める測度論

  • 6.1　測られるものたち（σ-加法族）と測るもの（測度）の定義
    • 6.1.1　σ-加法族の定義
    • 6.1.2　測度の定義
  • 6.2　σ-加法族の簡単な例
    • 6.2.1　有限集合上のσ-加法族
    • 6.2.2　一般の集合上のσ-加法族の簡単な例
    • 6.2.3　σ-加法族の大小関係
  • 6.3　測度の簡単な例
    • 6.3.1　自明な測度と有限集合上の測度
    • 6.3.2　有限分割を持つ集合上の測度
    • 6.3.3　ちょっと変わった測度（ディラック測度）

第7章　そして定義から性質を導く

  • 7.1　σ-加法族の性質を定義から導く
    • 7.1.1　もっともやさしい性質の証明
    • 7.1.2　色々な集合演算についても閉じていること
  • 7.2　測度の性質を定義から導く
    • 7.2.1　有限加法性
    • 7.2.2　単調性と劣加法性
    • 7.2.3　連続性

第8章　測度の構成という問題

  • 8.1　σ-加法族の構成
    • 8.1.1　集合族から生成されたσ-加法族
    • 8.1.2　σ-加法族より弱い集合族
  • 8.2　前測度から測度へ
    • 8.2.1　前測度の拡張としての測度
    • 8.2.2　拡張定理
    • 8.2.3　本質的な例：直線上の「長さ」とはなにか？
    • 8.2.4　ルベーグ測度の問題

［第4部　積分を再発明する̶ ルベーグ積分の世界］

第9章　ルベーグ積分

  • 9.1　リーマン積分からルベーグ積分へ
    • 9.1.1　積分の復習
    • 9.1.2　リーマン積分の弱点
    • 9.1.3　高さをコントロールする̶ ルベーグ積分のアイデア
  • 9.2　ルベーグ積分の構成
    • 9.2.1　可測関数
    • 9.2.2　単関数とその積分
    • 9.2.3　可測関数を単関数で近似する
    • 9.2.4　一般の積分
    • 9.2.5　ルベーグ積分の基本的な性質

第10章　ルベーグ積分の御利益の色々

  • 10.1　収束定理の色々
    • 10.1.1　単調収束定理
    • 10.1.2　収束定理のヴァリエーション
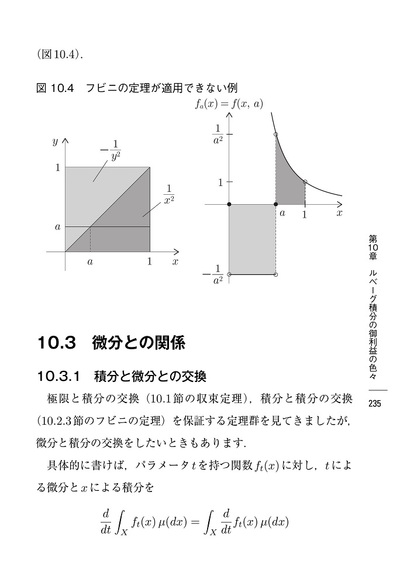
    • 10.1.3　収束定理が適用できない例
  • 10.2　フビニの定理
    • 10.2.1　具体的に：2次元のルベーグ測度
    • 10.2.2　抽象的に：直積測度
    • 10.2.3　フビニの定理
  • 10.3　微分との関係
    • 10.3.1　積分と微分との交換
    • 10.3.2　微積分学の基本定理
    • 10.3.3　ルベーグ積分論における微分学
    • 10.3.4　最後に
  • 参考文献
  • 索引

サポート

正誤表

本書の以下の部分に誤りがありました。ここに訂正するとともに，ご迷惑をおかけしたことを深くお詫び申し上げます。

（2024年3月21日最終更新）

P.71　真ん中の区間を表す式

誤 [1/9,1/3)
正 [2/9,1/3)

商品一覧